标签:个数 lda 聚集 ref 分离 矢量 nal 通过 绝对值
线性判别式分析(Linear Discriminant Analysis),简称为LDA。也称为Fisher线性判别(Fisher Linear Discriminant,FLD),是模式识别的经典算法,在1996年由Belhumeur引入模式识别和人工智能领域。
基本思想是将高维的模式样本投影到最佳鉴别矢量空间,以达到抽取分类信息和压缩特征空间维数的效果,投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离,即模式在该空间中有最佳的可分离性。
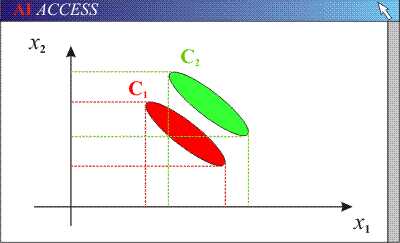
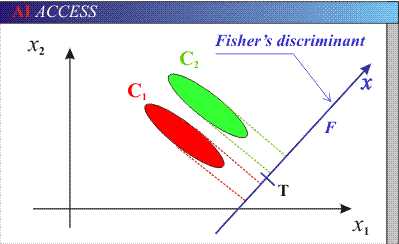
可以看到两个类别,一个绿色类别,一个红色类别。左图是两个类别的原始数据,现在要求将数据从二维降维到一维。直接投影到x1轴或者x2轴,不同类别之间会有重复,导致分类效果下降。右图映射到的直线就是用LDA方法计算得到的,可以看到,红色类别和绿色类别在映射之后之间的距离是最大的,而且每个类别内部点的离散程度是最小的(或者说聚集程度是最大的)。
PCA降维是直接和数据维度相关的,比如原始数据是n维的,那么PCA后,可以任意选取1维、2维,一直到n维都行(当然是对应特征值大的那些)。
LDA 降维是直接和类别的个数相关的,与数据本身的维度没关系,比如原始数据是n维的,一共有C个类别,那么LDA降维之后,一般就是1维,2维到C-1维进行选择(当然对应的特征值也是最大的一些),举个例子,假设图象分类,两个类别正例反例,每个图象10000维特征,那么LDA之后,就只有1维特征,并且这维特征的分类能力最好。
PS:对于很多两类分类的情况,LDA之后就剩下1维,找到分类效果最好的一个阈值貌似就可以了。
PCA投影的坐标系都是正交的,而LDA根据类别的标注,关注分类能力,因此不保证投影到的坐标系是正交的(一般都不正交)。
这一节,主要讨论只有两个类别的数据,LDA的计算。
现在要找到一个向量w,将数据x投影到w上去之后,得到新的数据y。
第一,为了实现投影后的两个类别的距离较远,用映射后两个类别的均值差的绝对值来度量。
第二,为了实现投影后,每个类内部数据点比较聚集,用投影后每个类别的方差来度量。
类别i的均值:
![]()
类别i投影后的均值(实际上等于mi的投影):
![]()
投影后均值差的绝对值:
![]()
投影后的方差(这里的y是类别i中数据投影后的数据,即y=w_t * x):
![]()
目标优化函数为:
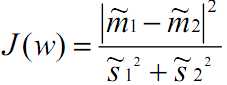
下面通过展开m‘和s‘,定义S_B和S_W:
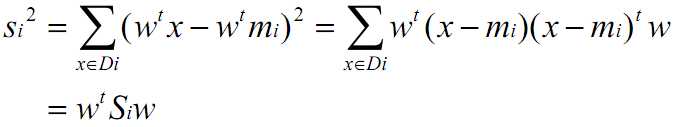
![]()
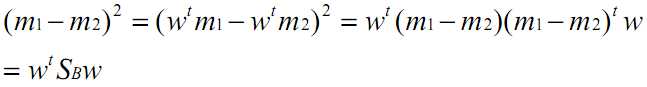
优化目标J(w)改写如下,这样是为了方便推导出计算w的方法。
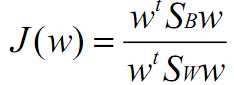
推导过程忽略了,最后推导结果如下:
![]()
假设数据是n维特征,m个数据,分类个数为2。那么Sw实际上是每个类别的协方差矩阵之和,每个类别的协方差矩阵都是n*n的,因此Sw是n*n的,m1-m2是n*1的。计算得到的w是n*1的,即w将维特征映射为1维。
PS:这里不用纠结与Sw的协方差矩阵形式,实际上这是拆拆开来w和w_t后的结果,实际上w*Sw*w_t后,仍旧是一个数值,即表示两个类的投影后方差之和。
对于S_w,就是“两个类别的协方差矩阵之和”变成了“多个类别的协方差矩阵之和”。
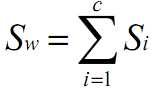
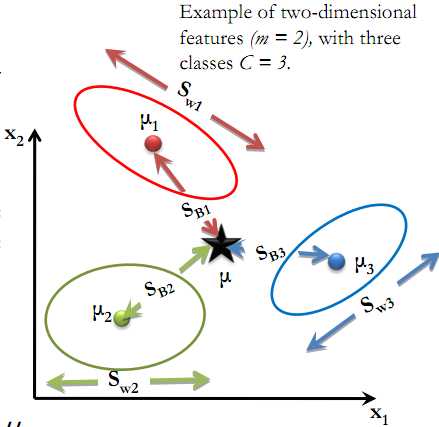
对于S_b,以前是“两个类别的均值之差的绝对值”,现在多个类别了,怎么计算呢?计算任意两个类别之间的均值之差的绝对值之和?这样对于N个类别,需要 C(N,2)次计算,这可能是一个方法,不过LDA使用的方法,计算每个类别的均值与所有类别均值的差异,并且对每个类别的数据量进行加权处理。下式中,m为所有类别的均值,m_i为类别i的均值,n_i为类别i的数据量。
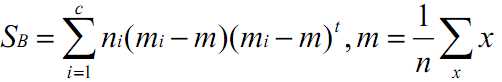
对于n维特征、C个类别、m个样本的数据,是将n维数据映射为C-1维。即所求的w是一个n*(c-1)的矩阵。S_w是一个n*n的矩阵(没有除以样本数的协方差矩阵之和),S_B是一个C*C的矩阵,实际上S_B矩阵的的秩最多是C-1,这是因为n_i*(m_i-m)这c向量实际上是线性相关的,因为他们的和是均值m的常数倍。这导致后面求解w,实际上是求出C-1个向量一个构成的一个w。
具体计算忽略。
如果原始数据投影后,仍旧不能很好的分开,那么Kernel LDA是一个解决方法。
LDA在计算量上与数据的维度有关,2DLDA能够大大减小LDA计算量。
第一,LDA最多投影出C-1维特征,如果需要更多特征,则要引入其他方法。
第二,LDA假设数据服从单峰高斯分布,比如下面的复杂数据结构。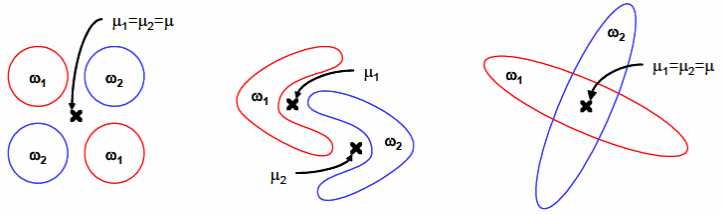
标签:个数 lda 聚集 ref 分离 矢量 nal 通过 绝对值
原文地址:http://www.cnblogs.com/zeze/p/6939521.html