标签:div 位向量法 src void 分享 blog for 跳过 状态压缩
紫书188子集生成,当时看不懂给跳过去了==
生成从0到n-1, n个数的子集
增量构造法,一次选出一个元素放到集合中,感觉是深度优先遍历解答树
void print_subset(int n, int* A, int cur) { for(int i = 0; i < cur; i++) printf("%d ", A[i]); printf("\n"); int s = cur ? A[cur-1]+1 : 0; for(int i = s; i < n; i++) { A[cur] = i; print_subset(n, A, cur+1); } }
甚至看输出能脑补递归的过程==
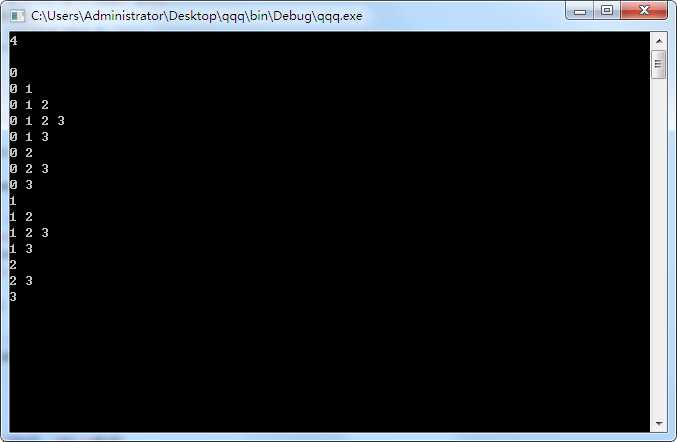
位向量法 其实就是用一个开关数组B,B【i】= 0或1表示子集中含不含i
void print_subset2(int n , int* B, int cur) { if(cur == n) { for(int i = 0; i < cur; i++) if(B[i]) printf("%d ", i); printf("\n"); return; } B[cur] = 1; print_subset2(n, B, cur+1); B[cur] = 0; print_subset2(n, B, cur+1); }
有点回溯法的意思,输出是这样的
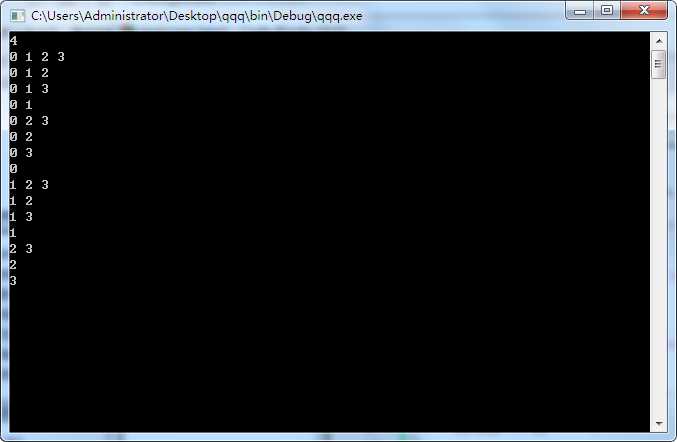
二进制法 位向量中每个元素都用0, 1表示太浪费了,不如用一个数的二进制形式表示,从右到左,第i位的0,1代表有没有i,i从0开始,(比如0101表示{0, 2})
(状态压缩初步)
void print_subset3(int n, int s) { for(int i = 0; i < n; i++) if(s&(1<<i)) printf("%d", i); printf("\n"); } void use3(int n) { for(int i = 1; i < (1<<n); i++) print_subset3(n, i); }
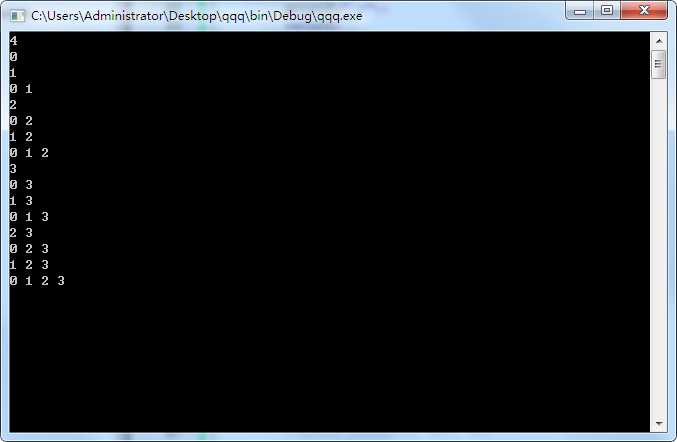
只是简单的生成0-n-1,生成给定集合或者集合有重复的话,改一改都可以做的
标签:div 位向量法 src void 分享 blog for 跳过 状态压缩
原文地址:http://www.cnblogs.com/DearDongchen/p/6940514.html