标签:公式 排序 独立 解决 联通 src 没有 处理 rmq
近日,微软新大楼的设计方案正在广泛征集中,其中一种方案格外引人注目。在这个方案中,大楼由 nn 栋楼组成,这些楼从左至右连成一排,编号依次为 11 到 nn,其中第 ii 栋楼有 h_ih?i??层。每栋楼的每一层为一个独立的 办公区域,可以步行 直达同层相邻楼栋的办公区域,以及 直达同楼栋相邻楼层的办公区域。
由于方案设计巧妙,上一层楼、下一层楼、向左右移动到相邻楼栋同层的办公区域均刚好需要 11 分钟。在这些办公区域中,有一些被 核心部门 占用了(一个办公区域内最多只有一个核心部门),出于工作效率的考虑,微软希望核心部门之间的移动时间越短越好。对于一个给定的 最大移动时间 kk,大楼的 协同值 定义为:有多少个 核心部门对 之间的移动时间不超过 kk。由于大楼门禁的限制,不可以走出整个大楼,也不可以登上天台思考人生。你可以认为在办公区域内的移动时间忽略不计,并且在大楼内总是按照最优方案进行移动。
对于一个给定的新大楼设计方案,你能算出方案的协同值么?
第一行包含两个正整数 n,k(1\leq k\leq 200020)n,k(1≤k≤200020),分别表示大楼的栋数以及最大移动时间。
第二行包含 nn 个正整数 h_1,h_2,...,h_n(1\leq h_i\leq 20)h?1??,h?2??,...,h?n??(1≤h?i??≤20),分别表示每栋楼的层数。
接下来一行包含一个正整数 mm,表示 核心部门 个数。
接下来 mm 行,每行两个正整数 x_i,y_i(1\leq x_i\leq n,1\leq y_i\leq h_{x_i})x?i??,y?i??(1≤x?i??≤n,1≤y?i??≤h?x?i????),表示该核心部门位于第 x_ix?i?? 栋楼的第 y_iy?i?? 层。
输入数据保证 mm 个核心部门的位置不会重复。
对于简单版本:1\leq n,m\leq 501≤n,m≤50;
对于中等版本:1\leq n\leq 200000,1\leq m\leq 20001≤n≤200000,1≤m≤2000;
对于困难版本:1\leq n,m\leq 2000001≤n,m≤200000。
输出一个整数,即整个大楼的 协同值。
样例对应题目描述中的图,核心部门 11 和核心部门 33 之间的距离为 8>78>7,因此不能计入答案。
5 7 4 1 1 3 1 3 1 4 3 1 4 3
2
首先我们必须知道怎么走最短
一开始我意识到这是个动态的情况,涉及多个变量
但这个问题好解决,如果答案关于多个变量单调,则我们可用树型数据结构快速求极值,线段树和ST表均可以
对于简单版本,数据范围小,上来写了个BFS,这没说的
但我们仔细观察一下就会发现,从一个部门走到另外一个部门,无非横向距离和纵向距离之加和
分开考虑的话,横向的距离一定不会超过|xa-xb|
纵向就值得思考了,由于观察到,
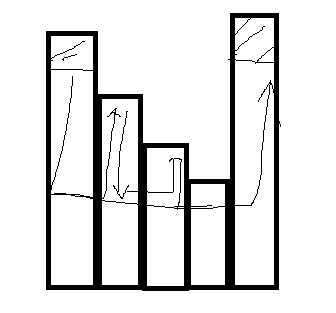
中间太高的楼层,上去是没有意义的,因为要联通才行,所以你提前上去是要走回头路的
对于这个题,只要不走回头路,也就是横纵的移动向量尽量重叠部分少就是最短的
然后你发现,如果你走到最下面那条线以下也是不好的,因为你还得上去
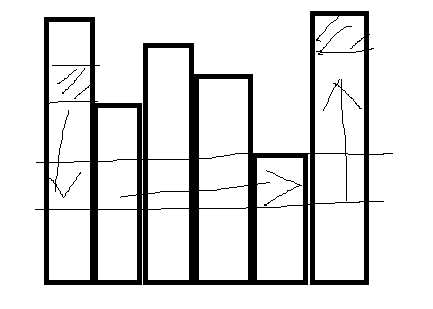
因此我们只要这三个方向的移动距离都加起来就好了
此处不妨设xb>xa
记hm=min{ya,yb,hxa,hxa+1,....,hxb}
则第一段是ya-hm+
第二段是xb-xa+
第三段是yb-hm
所以答案就是xb-xa+(ya+yb)-hm
利用RMQ,hm可以O(1)求出,预处理nlogn,排序mlogm,统计答案m^2,总复杂度,(nlogn+m^2)
标签:公式 排序 独立 解决 联通 src 没有 处理 rmq
原文地址:http://www.cnblogs.com/linkzijun/p/6944379.html