标签:mat 方式 cas assert ring 优化 不能 str swa
---------------------siwuxie095
索引从 1 开始
程序 1:最大堆的实现
MaxHeap.h:
#ifndef MAXHEAP_H #define MAXHEAP_H
#include <iostream> #include <algorithm> #include <string> #include <cmath> #include <cassert> using namespace std;
//最大堆:索引从1开始 template<typename Item> class MaxHeap {
private: Item *data; int count; int capacity;
//私有函数,用户不能调用 void shiftUp(int k) { //如果新添加的元素大于父节点的元素,则进行交换 while (k > 1 && data[k / 2] < data[k]) { swap(data[k / 2], data[k]); k /= 2; } }
//也是私有函数,用户不能调用 void shiftDown(int k) { //只要当前节点有孩子就进行循环 while (2 * k <= count) { // 在此轮循环中,data[k]和data[j]交换位置 int j = 2 * k;
// data[j]是data[2*k]和data[2*k+1]中的最大值 if (j + 1 <= count && data[j + 1] > data[j]) { j++; }
if (data[k] >= data[j]) { break; }
swap(data[k], data[j]); k = j; } }
public:
MaxHeap(int capacity) { //因为存储时是从索引1开始的,所以要加1 //即 多开辟一个空间 data = new Item[capacity + 1]; //计数器,这里索引等于计数器 count = 0; this->capacity = capacity; }
~MaxHeap() { delete []data; }
int size() { return count; }
bool isEmpty() { return count == 0; }
//向最大堆中添加新元素,新元素放在数组末尾 void insert(Item item) { //防止越界 assert(count + 1 <= capacity);
//索引从1开始 data[count + 1] = item; count++;
//新加入的元素有可能破坏最大堆的定义,需要通过 //Shift Up操作,把索引为count的元素尝试着向上 //移动来保持最大堆的定义 shiftUp(count); }
//取出最大堆中根节点的元素(最大值) Item extractMax() { //首先要保证堆不为空 assert(count > 0);
//取出根节点的元素(最大值) Item ret = data[1];
//将第一个元素(最大值)和最后一个元素进行交换 swap(data[1], data[count]);
//count--后,被取出的根节点就不用再考虑了 count--;
//调用Shift Down操作,想办法将此时的根节点(索引为1) //向下移动,来保持最大堆的定义 shiftDown(1);
return ret; }
public:
//在控制台打印测试用例 void testPrint() {
//限制:只能打印100个元素以内的堆,因为控制台一行的字符数量有限 if (size() >= 100) { cout << "Fancy print can only work for less than 100 int"; return; }
//限制:只能打印类型是int的堆 if (typeid(Item) != typeid(int)) { cout << "Fancy print can only work for int item"; return; }
cout << "The Heap size is: " << size() << endl; cout << "data in heap: "; for (int i = 1; i <= size(); i++) { cout << data[i] << " "; } cout << endl; cout << endl;
int n = size(); int max_level = 0; int number_per_level = 1; while (n > 0) { max_level += 1; n -= number_per_level; number_per_level *= 2; }
int max_level_number = int(pow(2, max_level - 1)); int cur_tree_max_level_number = max_level_number; int index = 1; for (int level = 0; level < max_level; level++) { string line1 = string(max_level_number * 3 - 1, ‘ ‘);
int cur_level_number = min(count - int(pow(2, level)) + 1, int(pow(2, level)));
bool isLeft = true;
for (int index_cur_level = 0; index_cur_level < cur_level_number; index++, index_cur_level++) { putNumberInLine(data[index], line1, index_cur_level, cur_tree_max_level_number * 3 - 1, isLeft);
isLeft = !isLeft; } cout << line1 << endl;
if (level == max_level - 1) { break; }
string line2 = string(max_level_number * 3 - 1, ‘ ‘); for (int index_cur_level = 0; index_cur_level < cur_level_number; index_cur_level++) { putBranchInLine(line2, index_cur_level, cur_tree_max_level_number * 3 - 1); }
cout << line2 << endl;
cur_tree_max_level_number /= 2; } }
private:
void putNumberInLine(int num, string &line, int index_cur_level, int cur_tree_width, bool isLeft) {
int sub_tree_width = (cur_tree_width - 1) / 2;
int offset = index_cur_level * (cur_tree_width + 1) + sub_tree_width;
assert(offset + 1 < line.size());
if (num >= 10) { line[offset + 0] = ‘0‘ + num / 10; line[offset + 1] = ‘0‘ + num % 10; } else { if (isLeft) line[offset + 0] = ‘0‘ + num; else line[offset + 1] = ‘0‘ + num; } }
void putBranchInLine(string &line, int index_cur_level, int cur_tree_width) {
int sub_tree_width = (cur_tree_width - 1) / 2;
int sub_sub_tree_width = (sub_tree_width - 1) / 2;
int offset_left = index_cur_level * (cur_tree_width + 1) + sub_sub_tree_width;
assert(offset_left + 1 < line.size());
int offset_right = index_cur_level * (cur_tree_width + 1) + sub_tree_width + 1 + sub_sub_tree_width;
assert(offset_right < line.size());
line[offset_left + 1] = ‘/‘; line[offset_right + 0] = ‘\\‘; } };
#endif |
main.cpp:
#include "MaxHeap.h" #include <ctime>
int main() {
MaxHeap<int> maxheap = MaxHeap<int>(100);
srand(time(NULL)); for (int i = 0; i < 15; i++) { maxheap.insert(rand() % 100); }
maxheap.testPrint();
cout << endl; while (!maxheap.isEmpty()) { cout << maxheap.extractMax() << " "; } cout << endl;
system("pause"); return 0; } |
运行一览:
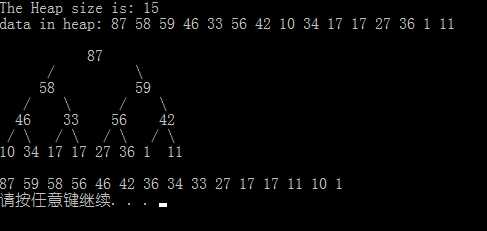
程序 2:最大堆的优化
MaxHeap.h:
#ifndef MAXHEAP_H #define MAXHEAP_H
#include <iostream> #include <algorithm> #include <string> #include <cmath> #include <cassert> using namespace std;
//最大堆:索引从1开始 template<typename Item> class MaxHeap {
private: Item *data; int count; int capacity;
//私有函数,用户不能调用 //使用插入排序的优化方式进行优化 void shiftUp(int k) { //如果新添加的元素大于父节点的元素,则进行交换 Item e = data[k]; while (k > 1 && data[k / 2] < e) { data[k] = data[k / 2]; k /= 2; } data[k] = e; }
//也是私有函数,用户不能调用 //使用插入排序的优化方式进行优化 void shiftDown(int k) { Item e = data[k]; //只要当前节点有孩子就进行循环 while (2 * k <= count) { // 在此轮循环中,data[k]和data[j]交换位置 int j = 2 * k;
// data[j]是data[2*k]和data[2*k+1]中的最大值 if (j + 1 <= count && data[j + 1] > data[j]) { j++; }
if (e >= data[j]) { break; }
data[k] = data[j]; k = j; } data[k] = e; }
public:
MaxHeap(int capacity) { //因为存储时是从索引1开始的,所以要加1 //即 多开辟一个空间 data = new Item[capacity + 1]; //计数器,这里索引等于计数器 count = 0; this->capacity = capacity; }
MaxHeap(Item arr[], int n) { data = new Item[n + 1]; capacity = n;
for (int i = 0; i < n; i++) { data[i + 1] = arr[i]; }
count = n;
//从最后一个非叶子节点的位置开始 for (int i = count / 2; i >= 1; i--) { //每次对索引为i的元素进行Shift Down操作 shiftDown(i); }
}
~MaxHeap() { delete []data; }
int size() { return count; }
bool isEmpty() { return count == 0; }
//向最大堆中添加新元素,新元素放在数组末尾 void insert(Item item) { //防止越界 assert(count + 1 <= capacity);
//索引从1开始 data[count + 1] = item; count++;
//新加入的元素有可能破坏最大堆的定义,需要通过 //Shift Up操作,把索引为count的元素尝试着向上 //移动来保持最大堆的定义 shiftUp(count); }
//取出最大堆中根节点的元素(最大值) Item extractMax() { //首先要保证堆不为空 assert(count > 0);
//取出根节点的元素(最大值) Item ret = data[1];
//将第一个元素(最大值)和最后一个元素进行交换 swap(data[1], data[count]);
//count--后,被取出的根节点就不用再考虑了 count--;
//调用Shift Down操作,想办法将此时的根节点(索引为1) //向下移动,来保持最大堆的定义 shiftDown(1);
return ret; }
public:
//在控制台打印测试用例 void testPrint() {
//限制:只能打印100个元素以内的堆,因为控制台一行的字符数量有限 if (size() >= 100) { cout << "Fancy print can only work for less than 100 int"; return; }
//限制:只能打印类型是int的堆 if (typeid(Item) != typeid(int)) { cout << "Fancy print can only work for int item"; return; }
cout << "The Heap size is: " << size() << endl; cout << "data in heap: "; for (int i = 1; i <= size(); i++) { cout << data[i] << " "; } cout << endl; cout << endl;
int n = size(); int max_level = 0; int number_per_level = 1; while (n > 0) { max_level += 1; n -= number_per_level; number_per_level *= 2; }
int max_level_number = int(pow(2, max_level - 1)); int cur_tree_max_level_number = max_level_number; int index = 1; for (int level = 0; level < max_level; level++) { string line1 = string(max_level_number * 3 - 1, ‘ ‘);
int cur_level_number = min(count - int(pow(2, level)) + 1, int(pow(2, level)));
bool isLeft = true;
for (int index_cur_level = 0; index_cur_level < cur_level_number; index++, index_cur_level++) { putNumberInLine(data[index], line1, index_cur_level, cur_tree_max_level_number * 3 - 1, isLeft);
isLeft = !isLeft; } cout << line1 << endl;
if (level == max_level - 1) { break; }
string line2 = string(max_level_number * 3 - 1, ‘ ‘); for (int index_cur_level = 0; index_cur_level < cur_level_number; index_cur_level++) { putBranchInLine(line2, index_cur_level, cur_tree_max_level_number * 3 - 1); }
cout << line2 << endl;
cur_tree_max_level_number /= 2; } }
private:
void putNumberInLine(int num, string &line, int index_cur_level, int cur_tree_width, bool isLeft) {
int sub_tree_width = (cur_tree_width - 1) / 2;
int offset = index_cur_level * (cur_tree_width + 1) + sub_tree_width;
assert(offset + 1 < line.size());
if (num >= 10) { line[offset + 0] = ‘0‘ + num / 10; line[offset + 1] = ‘0‘ + num % 10; } else { if (isLeft) line[offset + 0] = ‘0‘ + num; else line[offset + 1] = ‘0‘ + num; } }
void putBranchInLine(string &line, int index_cur_level, int cur_tree_width) {
int sub_tree_width = (cur_tree_width - 1) / 2;
int sub_sub_tree_width = (sub_tree_width - 1) / 2;
int offset_left = index_cur_level * (cur_tree_width + 1) + sub_sub_tree_width;
assert(offset_left + 1 < line.size());
int offset_right = index_cur_level * (cur_tree_width + 1) + sub_tree_width + 1 + sub_sub_tree_width;
assert(offset_right < line.size());
line[offset_left + 1] = ‘/‘; line[offset_right + 0] = ‘\\‘; } };
#endif |
main.cpp:
#include "MaxHeap.h" #include <ctime>
int main() {
MaxHeap<int> maxheap = MaxHeap<int>(100);
srand(time(NULL)); for (int i = 0; i < 15; i++) { maxheap.insert(rand() % 100); }
maxheap.testPrint();
cout << endl; while (!maxheap.isEmpty()) { cout << maxheap.extractMax() << " "; } cout << endl;
/*cout << endl; int arr[15]; for (int i = 0; i < 15; i++) { arr[i] = rand() % 100; } MaxHeap<int> maxheapx = MaxHeap<int>(arr, 15); maxheapx.testPrint(); cout << endl; while (!maxheapx.isEmpty()) { cout << maxheapx.extractMax() << " "; } cout << endl;*/
system("pause"); return 0; } |
运行一览:
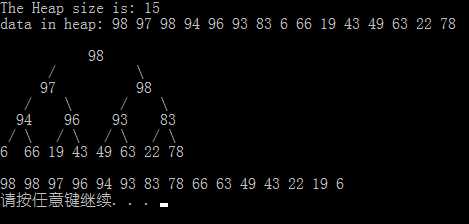
程序 3:最小堆的实现
MinHeap.h:
#ifndef MINHEAP_H #define MINHEAP_H
#include <iostream> #include <algorithm> #include <string> #include <cmath> #include <cassert> using namespace std;
//最小堆:索引从1开始 template<typename Item> class MinHeap {
private: Item *data; int count; int capacity;
//私有函数,用户不能调用 void shiftUp(int k) { //如果新添加的元素小于父节点的元素,则进行交换 while (k > 1 && data[k / 2] > data[k]) { swap(data[k / 2], data[k]); k /= 2; } }
//也是私有函数,用户不能调用 void shiftDown(int k) { //只要当前节点有孩子就进行循环 while (2 * k <= count) { // 在此轮循环中,data[k]和data[j]交换位置 int j = 2 * k;
// data[j]是data[2*k]和data[2*k+1]中的最小值 if (j + 1 <= count && data[j + 1] < data[j]) { j++; }
if (data[k] <= data[j]) { break; }
swap(data[k], data[j]); k = j; } }
public:
MinHeap(int capacity) { //因为存储时是从索引1开始的,所以要加1 //即 多开辟一个空间 data = new Item[capacity + 1]; //计数器,这里索引等于计数器 count = 0; this->capacity = capacity; }
~MinHeap() { delete []data; }
int size() { return count; }
bool isEmpty() { return count == 0; }
//向最小堆中添加新元素,新元素放在数组末尾 void insert(Item item) { //防止越界 assert(count + 1 <= capacity);
//索引从1开始 data[count + 1] = item; count++;
//新加入的元素有可能破坏最小堆的定义,需要通过 //Shift Up操作,把索引为count的元素尝试着向上 //移动来保持最小堆的定义 shiftUp(count); }
//取出最小堆中根节点的元素(最小值) Item extractMin() { //首先要保证堆不为空 assert(count > 0);
//取出根节点的元素(最小值) Item ret = data[1];
//将第一个元素(最小值)和最后一个元素进行交换 swap(data[1], data[count]);
//count--后,被取出的根节点就不用再考虑了 count--;
//调用Shift Down操作,想办法将此时的根节点(索引为1) //向下移动,来保持最小堆的定义 shiftDown(1);
return ret; }
public:
//在控制台打印测试用例 void testPrint() {
//限制:只能打印100个元素以内的堆,因为控制台一行的字符数量有限 if (size() >= 100) { cout << "Fancy print can only work for less than 100 int"; return; }
//限制:只能打印类型是int的堆 if (typeid(Item) != typeid(int)) { cout << "Fancy print can only work for int item"; return; }
cout << "The Heap size is: " << size() << endl; cout << "data in heap: "; for (int i = 1; i <= size(); i++) { cout << data[i] << " "; } cout << endl; cout << endl;
int n = size(); int max_level = 0; int number_per_level = 1; while (n > 0) { max_level += 1; n -= number_per_level; number_per_level *= 2; }
int max_level_number = int(pow(2, max_level - 1)); int cur_tree_max_level_number = max_level_number; int index = 1; for (int level = 0; level < max_level; level++) { string line1 = string(max_level_number * 3 - 1, ‘ ‘);
int cur_level_number = min(count - int(pow(2, level)) + 1, int(pow(2, level)));
bool isLeft = true;
for (int index_cur_level = 0; index_cur_level < cur_level_number; index++, index_cur_level++) { putNumberInLine(data[index], line1, index_cur_level, cur_tree_max_level_number * 3 - 1, isLeft);
isLeft = !isLeft; } cout << line1 << endl;
if (level == max_level - 1) { break; }
string line2 = string(max_level_number * 3 - 1, ‘ ‘); for (int index_cur_level = 0; index_cur_level < cur_level_number; index_cur_level++) { putBranchInLine(line2, index_cur_level, cur_tree_max_level_number * 3 - 1); }
cout << line2 << endl;
cur_tree_max_level_number /= 2; } }
private:
void putNumberInLine(int num, string &line, int index_cur_level, int cur_tree_width, bool isLeft) {
int sub_tree_width = (cur_tree_width - 1) / 2;
int offset = index_cur_level * (cur_tree_width + 1) + sub_tree_width;
assert(offset + 1 < line.size());
if (num >= 10) { line[offset + 0] = ‘0‘ + num / 10; line[offset + 1] = ‘0‘ + num % 10; } else { if (isLeft) line[offset + 0] = ‘0‘ + num; else line[offset + 1] = ‘0‘ + num; } }
void putBranchInLine(string &line, int index_cur_level, int cur_tree_width) {
int sub_tree_width = (cur_tree_width - 1) / 2;
int sub_sub_tree_width = (sub_tree_width - 1) / 2;
int offset_left = index_cur_level * (cur_tree_width + 1) + sub_sub_tree_width;
assert(offset_left + 1 < line.size());
int offset_right = index_cur_level * (cur_tree_width + 1) + sub_tree_width + 1 + sub_sub_tree_width;
assert(offset_right < line.size());
line[offset_left + 1] = ‘/‘; line[offset_right + 0] = ‘\\‘; } };
#endif |
main.cpp:
#include "MinHeap.h" #include <ctime>
int main() {
MinHeap<int> minheap = MinHeap<int>(100);
srand(time(NULL)); for (int i = 0; i < 15; i++) { minheap.insert(rand() % 100); }
minheap.testPrint();
cout << endl; while (!minheap.isEmpty()) { cout << minheap.extractMin() << " "; } cout << endl;
system("pause"); return 0; } |
运行一览:
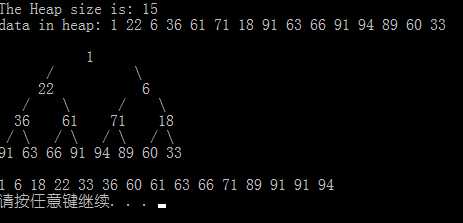
程序 4:最小堆的优化
MinHeap.h:
#ifndef MINHEAP_H #define MINHEAP_H
#include <iostream> #include <algorithm> #include <string> #include <cmath> #include <cassert> using namespace std;
//最小堆:索引从1开始 template<typename Item> class MinHeap {
private: Item *data; int count; int capacity;
//私有函数,用户不能调用 //使用插入排序的优化方式进行优化 void shiftUp(int k) { Item e = data[k]; //如果新添加的元素小于父节点的值, //则和父节点的值进行交换,即上升 while (k > 1 && data[k / 2] > e) { data[k] = data[k / 2]; k /= 2; } data[k] = e; }
//也是私有函数,用户不能调用 //使用插入排序的优化方式进行优化 void shiftDown(int k) { Item e = data[k]; //只要当前节点有孩子就进行循环 while (2 * k <= count) { // 在此轮循环中,data[k]和data[j]交换位置 int j = 2 * k;
// data[j]是data[2*k]和data[2*k+1]中的最小值 if (j + 1 <= count && data[j + 1] < data[j]) { j++; }
if (e <= data[j]) { break; }
data[k] = data[j]; k = j; } data[k] = e; }
public:
MinHeap(int capacity) { //因为存储时是从索引1开始的,所以要加1 //即 多开辟一个空间 data = new Item[capacity + 1]; //计数器,这里索引等于计数器 count = 0; this->capacity = capacity; }
MinHeap(Item arr[], int n) { data = new Item[n + 1]; capacity = n;
for (int i = 0; i < n; i++) { data[i + 1] = arr[i]; }
count = n;
//从最后一个非叶子节点的位置开始 for (int i = count / 2; i >= 1; i--) { //每次对索引为i的元素进行Shift Down操作 shiftDown(i); }
}
~MinHeap() { delete []data; }
int size() { return count; }
bool isEmpty() { return count == 0; }
//向最小堆中添加新元素,新元素放在数组末尾 void insert(Item item) { assert(count + 1 <= capacity);
//索引从1开始 data[count + 1] = item; count++;
//新加入的元素有可能破坏最小堆的定义,需要通过 //Shift Up操作,把索引为count的元素尝试着向上 //移动来保持最小堆的定义 shiftUp(count); }
//取出最小堆中根节点的元素(最小值) Item extractMin() { //首先要保证堆不为空 assert(count > 0);
//取出根节点的元素(最小值) Item ret = data[1];
//将第一个元素(最小值)和最后一个元素进行交换 swap(data[1], data[count]);
//count--后,被取出的根节点就不用再考虑了 count--;
//调用Shift Down操作,想办法将此时的根节点(索引为1) //向下移动,来保持最小堆的定义 shiftDown(1);
return ret; }
public:
//在控制台打印测试用例 void testPrint() {
//限制:只能打印100个元素以内的堆,因为控制台一行的字符数量有限 if (size() >= 100) { cout << "Fancy print can only work for less than 100 int"; return; }
//限制:只能打印类型是int的堆 if (typeid(Item) != typeid(int)) { cout << "Fancy print can only work for int item"; return; }
cout << "The Heap size is: " << size() << endl; cout << "data in heap: "; for (int i = 1; i <= size(); i++) { cout << data[i] << " "; } cout << endl; cout << endl;
int n = size(); int max_level = 0; int number_per_level = 1; while (n > 0) { max_level += 1; n -= number_per_level; number_per_level *= 2; }
int max_level_number = int(pow(2, max_level - 1)); int cur_tree_max_level_number = max_level_number; int index = 1; for (int level = 0; level < max_level; level++) { string line1 = string(max_level_number * 3 - 1, ‘ ‘);
int cur_level_number = min(count - int(pow(2, level)) + 1, int(pow(2, level)));
bool isLeft = true;
for (int index_cur_level = 0; index_cur_level < cur_level_number; index++, index_cur_level++) { putNumberInLine(data[index], line1, index_cur_level, cur_tree_max_level_number * 3 - 1, isLeft);
isLeft = !isLeft; } cout << line1 << endl;
if (level == max_level - 1) { break; }
string line2 = string(max_level_number * 3 - 1, ‘ ‘); for (int index_cur_level = 0; index_cur_level < cur_level_number; index_cur_level++) { putBranchInLine(line2, index_cur_level, cur_tree_max_level_number * 3 - 1); }
cout << line2 << endl;
cur_tree_max_level_number /= 2; } }
private:
void putNumberInLine(int num, string &line, int index_cur_level, int cur_tree_width, bool isLeft) {
int sub_tree_width = (cur_tree_width - 1) / 2;
int offset = index_cur_level * (cur_tree_width + 1) + sub_tree_width;
assert(offset + 1 < line.size());
if (num >= 10) { line[offset + 0] = ‘0‘ + num / 10; line[offset + 1] = ‘0‘ + num % 10; } else { if (isLeft) line[offset + 0] = ‘0‘ + num; else line[offset + 1] = ‘0‘ + num; } }
void putBranchInLine(string &line, int index_cur_level, int cur_tree_width) {
int sub_tree_width = (cur_tree_width - 1) / 2;
int sub_sub_tree_width = (sub_tree_width - 1) / 2;
int offset_left = index_cur_level * (cur_tree_width + 1) + sub_sub_tree_width;
assert(offset_left + 1 < line.size());
int offset_right = index_cur_level * (cur_tree_width + 1) + sub_tree_width + 1 + sub_sub_tree_width;
assert(offset_right < line.size());
line[offset_left + 1] = ‘/‘; line[offset_right + 0] = ‘\\‘; } };
#endif |
main.cpp:
#include "MinHeap.h" #include <ctime>
int main() {
MinHeap<int> minheap = MinHeap<int>(100);
srand(time(NULL)); for (int i = 0; i < 15; i++) { minheap.insert(rand() % 100); }
minheap.testPrint();
cout << endl; while (!minheap.isEmpty()) { cout << minheap.extractMin() << " "; } cout << endl;
/*cout << endl; int arr[15]; for (int i = 0; i < 15; i++) { arr[i] = rand() % 100; } MinHeap<int> minheapx = MinHeap<int>(arr, 15); minheapx.testPrint(); cout << endl; while (!minheapx.isEmpty()) { cout << minheapx.extractMin() << " "; } cout << endl;*/
system("pause"); return 0; } |
运行一览:
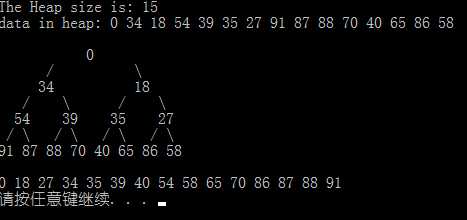
【made by siwuxie095】
标签:mat 方式 cas assert ring 优化 不能 str swa
原文地址:http://www.cnblogs.com/siwuxie095/p/6947041.html