Subsets系列

时间：2014-08-28 17:58:05 阅读：356 评论：0 收藏：0 [点我收藏+]

标签：des style blog http color os 使用 io strong

Subsets

Given a set of distinct integers, S, return all possible subsets.

Note:

Elements in a subset must be in non-descending order.
The solution set must not contain duplicate subsets.

For example,
If S = [1,2,3], a solution is:

[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

方法一：使用深度搜索，对于每个元素都有选择和不选择两种情况，那么我们就一次遍历这个数组，每个元素我们都有两个分支，一是不选择，另一个是选择，代码如下：

 1 class Solution {
 2 public:
 3     vector<vector<int> > subsets(vector<int> &S) {
 4         sort(S.begin(), S.end());   //题目要求非递减，所以先排序
 5         vector<int> path;   //记录对数组元素的选择情况
 6         dfs(S, path, 0);
 7         return allpath;
 8     }
 9     
10     void dfs(vector<int>& S, vector<int>& path, int k) {
11         if( k == S.size() ) {   //当k个元素都被选择完毕
12             allpath.push_back(path);    //那么这就是其中一个子集
13             return ;
14         }
15         dfs(S, path, k+1);  //不选择第k个元素
16         path.push_back(S[k]);   //放入path中
17         dfs(S, path, k+1);  //选择第k个元素
18         path.pop_back();    //取出
19     }
20     
21 private:
22     vector< vector<int> > allpath;  //存放所有的子集
23 };

方法二：分析上面的dfs方法，如下图：

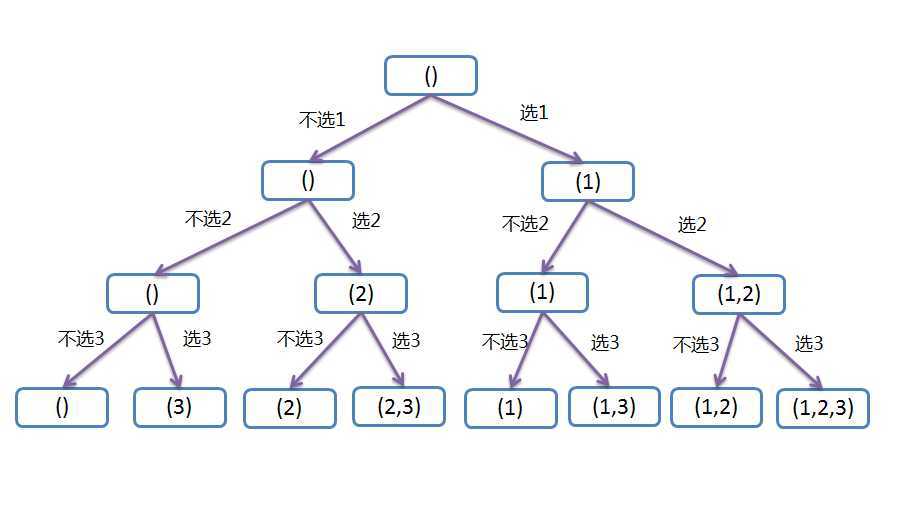
bubuko.com,布布扣

第一层是()

第二层是在第一层的基础上，每个元素都加上1，合起来就是()，(1)

第三层是是在第二层的基础上，每个元素都加上2，合起来就是()，(1)，(2)，(1,2)

第四层就是在第三层的基础上，每个元素都加上3，合起来就是()，(1)，(2)，(1,2)，(3)，(1,3)，(2,3)，(1,2,3)

因此迭代的方式容易得出了，代码如下：

 1 class Solution {
 2 public:
 3     vector<vector<int> > subsets(vector<int> &S) {
 4         vector< vector<int> > ans;
 5         sort(S.begin(), S.end());   //答案要求非递减，因此需要排序
 6         ans.push_back( vector<int>() ); //首先放入空集，此时ans存放得时第一层的结果
 7         for(int i=0; i<S.size(); ++i) { //迭代n个元素
 8             int presize = ans.size();   //标记上层的结果的个数
 9             for(int j=0; j<presize; ++j) {  //上层每个元素取出，并加上S[i]，再放入下层的结果中，就得到了下层的结果
10                 vector<int> tv = ans[j];
11                 tv.push_back(S[i]);
12                 ans.push_back(tv);
13             }
14         }
15         return ans;
16     }
17 };

方法三：使用二进制来模拟子集，数组元素为123，那么010，表示1不选，2选，3不选，依次遍历二进制就可以获取原集合的所有子集，代码如下：

 1 class Solution {
 2 public:
 3     vector<vector<int> > subsets(vector<int> &S) {
 4         vector< vector<int> > ans;
 5         sort(S.begin(), S.end());   //答案要求非递减，因此需要排序
 6         int len = S.size();
 7         unsigned long long maxbits = 1<<len;    //设置二进制数上限
 8         while( --maxbits ) {    //遍历每个二进制值，然后在根据i位的值是1还是0，来选择还是不选择S[i]
 9             vector<int> tv;
10             for(int i=0; i<len; ++i)    //依次扫描n位
11                 if( 1<<i & maxbits ) {
12                     tv.push_back(S[i]);
13                 }
14             ans.push_back(tv);
15         }
16         ans.push_back( vector<int>() ); //maxbits为0跳出循环，没有放入空集，因此需要放入空集
17         return ans;
18     }
19 };

注：代码有bug，如果元素个数超过64个....那么就会出现异常，解决方案是开数组，模拟二进制进位。。。。

Subsets II

Given a collection of integers that might contain duplicates, S, return all possible subsets.

Note:

Elements in a subset must be in non-descending order.
The solution set must not contain duplicate subsets.

For example,
If S = [1,2,2], a solution is:

[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

方法一：先按照无重复元素进行计算，然后在结果中去重，比较暴力。

方法二：分析1222数组子集生成流程，如下：

bubuko.com,布布扣

第一层为空集，第一层为()

第二层为在第一层基础上直接加1，第二层结果为(), (1)

第三层为在第二层基础上直接加2，第三层结果为(), (1), (2), (1,2)

第四层在第三层的基础上，挑选了(2)，(1,2)加2，最后第四层为(), (1), (2), (1,2), (2,2), (1,2,2)

第五层在第四层的基础上，挑选了(2,2), (1,2,2)加2，最后第五层为(), (1), (2), (1,2), (2,2), (1,2,2), (2,2,2), (1,2,2,2)

故 排序后，当前处理的数字在前面出现了k次，那么只能在已经出现k次该数的集合上添加该数

则递归的方法如下：

 1 class Solution {
 2 public:
 3     vector<vector<int> > subsetsWithDup(vector<int> &S) {
 4         sort(S.begin(), S.end());
 5         vector<int> path;
 6         ans.clear();
 7         dfs(S, path, 0);
 8         return ans;
 9     }
10     
11     void dfs(vector<int>& S, vector<int>& path, int k) {
12         if( k == S.size() ) {
13             ans.push_back(path);
14             return ;
15         }
16         int presame = k;
17         while( presame >= 0 && S[presame] == S[k] ) --presame;  //往左边寻找第一个不同于S[k]元素
18         int samenum = k - presame - 1;  //在第k个数前面与S[k]相同元素的个数
19         if( samenum == 0    //若没有相同的元素
20             || ( path.size() >= samenum && path[path.size()-samenum] == S[k] )  //出现samenum个相同元素的集合
21             ) {
22             path.push_back(S[k]);   //那么选择S[k]
23             dfs(S, path, k+1);
24             path.pop_back();
25         }
26         dfs(S, path, k+1);  //不选择S[k]
27     }
28     
29 private:
30     vector< vector<int> > ans;
31 };

迭代的方法如下：

 1 class Solution {
 2 public:
 3     vector<vector<int> > subsetsWithDup(vector<int> &S) {
 4         sort(S.begin(), S.end());
 5         vector< vector<int> > ans;
 6         ans.push_back( vector<int>() ); //放入空集
 7         int preInt = S[0]; //前一个被访问的元素
 8         int needSelectSubsets = 1;  //如果当前数组在前面出现k次，那么这个值表示含有k个相同元素的子集
 9         for(int i=0; i<S.size(); ++i) {
10             if( S[i] != preInt ) {  //如果不等，直接更新
11                 preInt = S[i];
12                 needSelectSubsets = ans.size();
13             }
14             int len = ans.size();
15             for(int j = len - needSelectSubsets; j<len; ++j) {  //ans中后面needSelectSubsets个子集满足添加元素条件
16                 vector<int> tv = ans[j];
17                 tv.push_back(S[i]);
18                 ans.push_back(tv);
19             }
20         }
21         return ans;
22     }
23 };

Subsets系列

标签：des style blog http color os 使用 io strong

原文地址：http://www.cnblogs.com/bugfly/p/3942002.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行