标签:红黑树 fine getch upd include bsp www ios 最大值
将Treap按照权值或排名分裂为两棵Treap 我只写了按权值分裂
对于我们遍历到每一个点,假如它的权值小于k,那么它的所有左子树,都要分到左边的树里,然后遍历它的右儿子。假如大于k,把它的所有右子树分到右边的树里,遍历左儿子。
因为它的最多操作次数就是一直分到底,效率就是O(logn)。
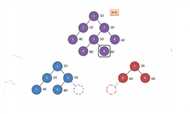
void split(int now,int k,int &x,int &y) { if(!now) x=y=0; else { if(val[now]<=k) x=now,split(ch[now][1],k,ch[now][1],y); else y=now,split(ch[now][0],k,x,ch[now][0]); update(now); } }
这个就是把两个Treap合成一个,保证第一个的权值小于第二个。
因为第一个Treap的权值都比较小,我们比较一下它的fix(附加权值),假如第一个的fix小,我们就可以直接保留它的所有左子树,接着把第一个Treap变成它的右儿子。反之,我们可以保留第二棵的所有右子树,指针指向左儿子。
你可以把这个过程形象的理解为在第一个Treap的左子树上插入第二个树,也可以理解为在第二个树的左子树上插入第一棵树。因为第一棵树都满足小于第二个树,所以就变成了比较fix来确定树的形态。
也就是说,我们其实是遍历了第一个trep的根->最大节点,第二个Treap的根->最小节点,也就是O(logn)
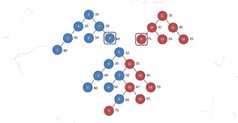
int merge(int A,int B) { if(!A||!B) return A+B; if(fix[A]<fix[B]){ch[A][1]=merge(ch[A][1],B); update(A); return A;} else {ch[B][0]=merge(A,ch[B][0]); update(B); return B;} }
下面我们就可以通过这两个基本的东西实现各种各样的操作了。
插入一个权值为v的点,把树按照v的权值split成两个,再按照顺序merge回去。
删除权值为v的点,把树按照v分成两个a,b,再把a按照v-1分成c,d。把c的两个子儿子merge起来,再merge(merge(c,d),b)
(因为把c的两个儿子merge起来之后,如果权值为v的节点有一个,就已经把他删除了,因为merge后c=0;若有多个就删除了一个)
找前驱的话把root按v-1 split成x,y,在x里面找最大值
找后继的话把root按v split成x,y,在y里找最小值
把root按v-1 split成x,y,排名是x的siz
代码:https://www.luogu.org/problem/show?pid=3369 普通平衡树
#include<iostream> #include<cstdio> #include<cstring> #include<ctime> #include<cstdlib> #define maxn 500001 using namespace std; int size[maxn],ch[maxn][2],fix[maxn],val[maxn]; int T,cnt,n,m,x,y,z,p,a,root,com; inline int read() { int x=0,f=1;char c=getchar(); while(c>‘9‘||c<‘0‘){if(c==‘-‘)f=-1;c=getchar();} while(c>=‘0‘&&c<=‘9‘){x=x*10+c-‘0‘;c=getchar();} return x*f; } inline void update(int x) { size[x]=1+size[ch[x][0]]+size[ch[x][1]]; } inline int new_node(int x) { size[++cnt]=1; val[cnt]=x; fix[cnt]=rand(); return cnt; } int merge(int A,int B) { if(!A||!B) return A+B; if(fix[A]<fix[B]){ch[A][1]=merge(ch[A][1],B); update(A); return A;} else {ch[B][0]=merge(A,ch[B][0]); update(B); return B;} } void split(int now,int k,int &x,int &y) { if(!now) x=y=0; else { if(val[now]<=k) x=now,split(ch[now][1],k,ch[now][1],y); else y=now,split(ch[now][0],k,x,ch[now][0]); update(now); } } int kth(int now,int k) { while(1) { if(k<=size[ch[now][0]]) now=ch[now][0]; else if(k==size[ch[now][0]]+1) return now; else k-=size[ch[now][0]]+1,now=ch[now][1]; } } int main() { srand((unsigned)time(NULL)); T=read(); while(T--) { p=read();a=read(); if(p==1) { split(root,a,x,y); root=merge(merge(x,new_node(a)),y); } else if(p==2) { split(root,a,x,z); split(x,a-1,x,y); y=merge(ch[y][0],ch[y][1]); root=merge(merge(x,y),z); } else if(p==3) { split(root,a-1,x,y); printf("%d\n",size[x]+1); root=merge(x,y); } else if(p==4) printf("%d\n",val[kth(root,a)]); else if(p==5) { split(root,a-1,x,y); printf("%d\n",val[kth(x,size[x])]); root=merge(x,y); } else { split(root,a,x,y); printf("%d\n",val[kth(y,1)]); root=merge(x,y); } } return 0; }
可持久化Treap(fhq Treap,非旋转式Treap)学习(未完待续)
标签:红黑树 fine getch upd include bsp www ios 最大值
原文地址:http://www.cnblogs.com/L-Memory/p/6949756.html