神经网络激励函数

标签：plot   htm   坐标   缺点   更新   常见   权重   play   5.5   

常用激励函数

每一次输入和权重w线性组合之后，都会通过一个激励函数(也可以叫做非线性激励函数)，经非线性变换后输出。实际的神经网络中有一些可选的激励函数，我们一一说明一下最常见的几种：

1 sigmoid

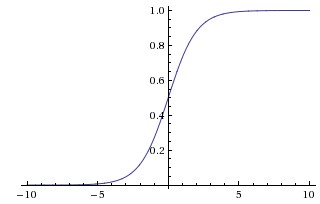
sigmoid函数提到的次数太多，相信大家都知道了。数学形式很简单，是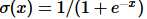σ(x)=1/(1+e?x)，图像如上图所示，功能是把一个实数压缩至0到1之间。输入的数字非常大的时候，结果会接近1，而非常大的负数作为输入，则会得到接近0的结果。不得不说，早期的神经网络中，sigmoid函数作为激励函数使用非常之多，因为大家觉得它很好地解释了神经元受到刺激后是否被激活和向后传递的场景(从几乎没有被激活，也就是0，到完全被激活，也就是1)。不过似乎近几年的实际应用场景中，比较少见到它的身影，它主要的缺点有2个：

• sigmoid函数在实际梯度下降中，容易饱和和终止梯度传递。我们来解释一下，大家知道反向传播过程，依赖于计算的梯度，在一元函数中，即斜率。而在sigmoid函数图像上，大家可以很明显看到，在纵坐标接近0和1的那些位置(也就是输入信号的幅度很大的时候)，斜率都趋于0了。我们回想一下反向传播的过程，我们最后用于迭代的梯度，是由中间这些梯度值结果相乘得到的，因此如果中间的局部梯度值非常小，直接会把最终梯度结果拉近0，也就是说，残差回传的过程，因为sigmoid函数的饱和被杀死了。说个极端的情况，如果一开始初始化权重的时候，我们取值不是很恰当，而激励函数又全用的sigmoid函数，那么很有可能神经元一个不剩地饱和到无法学习，整个神经网络也根本没办法训练起来。
• sigmoid函数的输出没有0中心化，这是一个比较闹心的事情，因为每一层的输出都要作为下一层的输入，而未0中心化会直接影响梯度下降，我们这么举个例子吧，如果输出的结果均值不为0，举个极端的例子，全部为正的话(例如f=W^TX+Bf=wTx+b中所有x>0x>0)，那么反向传播回传到ww上的梯度将要么全部为正要么全部为负(取决于f的梯度正负性)，这带来的后果是，反向传播得到的梯度用于权重更新的时候，不是平缓地迭代变化，而是类似锯齿状的突变。当然，要多说一句的是，这个缺点相对于第一个缺点，还稍微好一点，第一个缺点的后果是，很多场景下，神经网络根本没办法学习。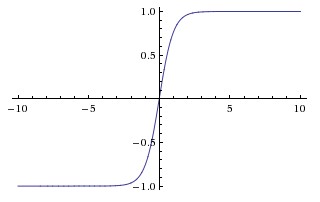

2 Tanh

Tanh函数的图像如上图所示。它会将输入值压缩至-1到1之间，当然，它同样也有sigmoid函数里说到的第一个缺点，在很大或者很小的输入值下，神经元很容易饱和。但是它缓解了第二个缺点，它的输出是0中心化的。所以在实际应用中，tanh激励函数还是比sigmoid要用的多一些的。

3 ReLU

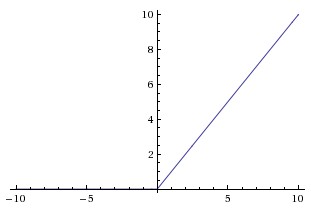
ReLU是修正线性单元(The Rectified Linear Unit)的简称，近些年使用的非常多，图像如上图所示。它对于输入x计算f(x)=max(0,x)f(x)=max(0,x)。换言之，以0为分界线，左侧都为0，右侧是y=x这条直线。

它有它对应的优势，也有缺点：

• 优点1：实验表明，它的使用，相对于sigmoid和tanh，可以非常大程度地提升随机梯度下降的收敛速度。不过有意思的是，很多人说，这个结果的原因是它是线性的，而不像sigmoid和tanh一样是非线性的。具体的收敛速度结果对比如下图，收敛速度大概能快上6倍：
  
  
  
• 优点2：相对于tanh和sigmoid激励神经元，求梯度不要简单太多好么！！！毕竟，是线性的嘛。。。
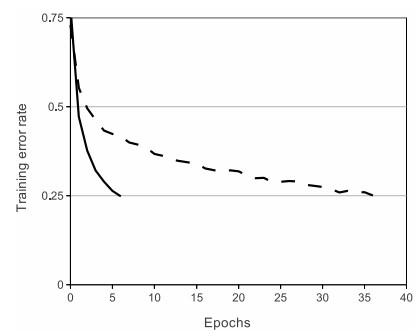
• 缺点1：ReLU单元也有它的缺点，在训练过程中，它其实挺脆弱的，有时候甚至会挂掉。举个例子说吧，如果一个很大的梯度流经ReLU单元，那权重的更新结果可能是，在此之后任何的数据点都没有办法再激活它了。一旦这种情况发生，那本应经这个ReLU回传的梯度，将永远变为0。当然，这和参数设置有关系，所以我们要特别小心，再举个实际的例子哈，如果学习速率被设的太高，结果你会发现，训练的过程中可能有高达40%的ReLU单元都挂掉了。所以我们要小心设定初始的学习率等参数，在一定程度上控制这个问题。

4 Leaky ReLU

上面不是提到ReLU单元的弱点了嘛，所以孜孜不倦的ML researcher们，就尝试修复这个问题咯，他们做了这么一件事，在x<0的部分，leaky ReLU不再让y的取值为0了，而是也设定为一个坡度很小(比如斜率0.01)的直线。f(x)因此是一个分段函数，x<0时，f(x)=axf(x)=αx(aα是一个很小的常数)，x>0时，f(x)=xf(x)=x。有一些researcher们说这样一个形式的激励函数帮助他们取得更好的效果，不过似乎并不是每次都比ReLU有优势。

5 Maxout

也有一些其他的激励函数，它们并不是对W^TX+BWTX+b做非线性映射f(W^TX+b)f(WTX+b)。一个近些年非常popular的激励函数是Maxout(详细内容请参见Maxout)。简单说来，它是ReLU和Leaky ReLU的一个泛化版本。对于输入x，Maxout神经元计算max(w₁^Tx+b_1,w₂^Tx+b₁)max(wT1x+b1,wT2x+b2)。有意思的是，如果你仔细观察，你会发现ReLU和Leaky ReLU都是它的一个特殊形式(比如ReLU，你只需要把w₁,b₁w1,b1设为0)。因此Maxout神经元继承了ReLU单元的优点，同时又没有『一不小心就挂了』的担忧。如果要说缺点的话，你也看到了，相比之于ReLU，因为有2次线性映射运算，因此计算量也double了。

6、激励函数/神经元小总结

以上就是我们总结的常用的神经元和激励函数类型。顺便说一句，即使从计算和训练的角度看来是可行的，实际应用中，其实我们很少会把多种激励函数混在一起使用。

那我们咋选用神经元/激励函数呢？一般说来，用的最多的依旧是ReLU，但是我们确实得小心设定学习率，同时在训练过程中，还得时不时看看神经元此时的状态(是否还『活着』)。当然，如果你非常担心神经元训练过程中挂掉，你可以试试Leaky ReLU和Maxout。额，少用sigmoid老古董吧，有兴趣倒是可以试试tanh，不过话说回来，通常状况下，它的效果不如ReLU/Maxout。

神经网络激励函数

标签：plot   htm   坐标   缺点   更新   常见   权重   play   5.5   

原文地址：http://www.cnblogs.com/xinbaby829/p/6953386.html