标签：因子 alt 表示 而且 bfd 变换 误差 均方误差 循环
时域：
----------------------------------------------------------------------------------------------------------------------
LMS滤波器
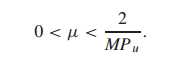
参数更新公式：
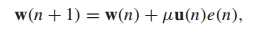
权重更新收到输入信号的能量影响较大，输入信号能量越大，步长取值应该较小，保证不容易发散。
步长太大，容易发散。
步长太小，稳定，但是收敛速度慢，相互矛盾。
缺点：
1.逐个点更新，计算量大
2.瞬时跟踪能力较弱
NLMS滤波器
将输入信号的能量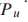
融合入权重更新公式，则
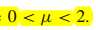
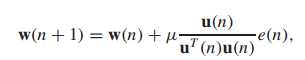
优点：对于不太平稳的语音，相对LMS，也有较快的收敛性和平稳性。
计算量问题：
LMS算法：M阶自适应滤波器作用，有M次乘法，权重因子更新，则有M+1次乘法。M阶滤波器走一圈，则有2M+1次乘法。
NLMS算法：需要加上额外的能量乘法计算，则有3M+2次乘法。
计算量都正比于M阶系数。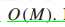
对于NLMS中能量的计算，可以用平均能量做平滑进行估计，减小计算量：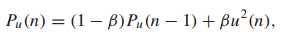
AP算法：NLMS的一般化
利用了P列历史数据，后续的参数计算都是矩阵计算，不再是逐个点计算。有更好更快的收敛性，但是 计算量变大为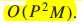
重复利用过去的数据来提高收敛速度，但数据重用也导致了计算复杂度的增大。
当P为1时，退化成NLMS。
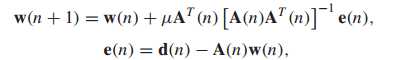
RLS算法：最小化加权重的均方误差和。
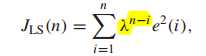
越久的点，则占的权重就越小，符合实际情况，满足非平稳的特性。
更新公式：
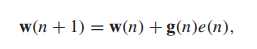
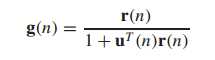其中，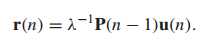
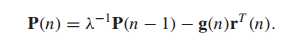
复杂度：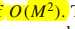
----------------------------------------------------------------------------------------------------------------------
可变步长：
----------------------------------------------------------------------------------------------------------------------
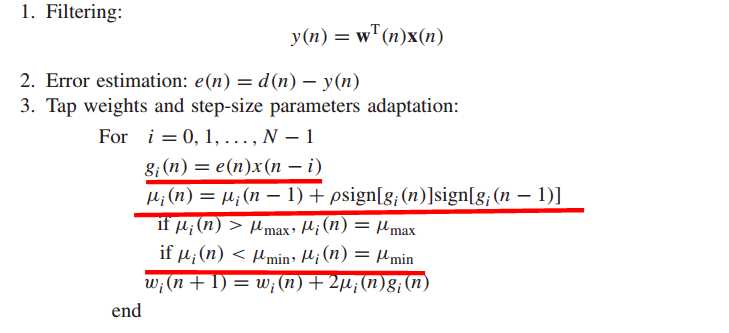
时延估计：
DTD检测：
http://www.docin.com/p-1263426732.html
http://www.docin.com/p-848898417.html&dpage=1&key=%E5%9B%9E%E9%9F%B3%E6%80%8E%E4%B9%88%E6%B2%BB
《一种新的回音消除的双向通话检测算法》
能量比较法
GEIGEL法 简单误判率高
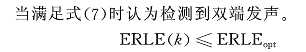
相关函数法 计算量大
回声路径估计法 复杂
两矢量夹角法 就是下面那个公式
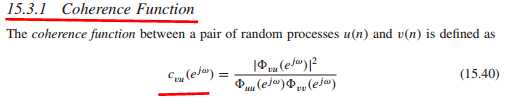
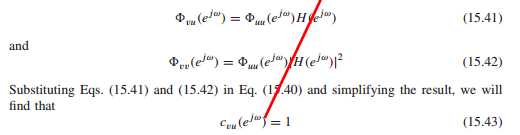
如果v(n)由u(n)经过线性系统获得，则该系数为1，表示两者之间的线性关系，相关度。
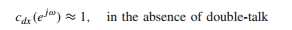
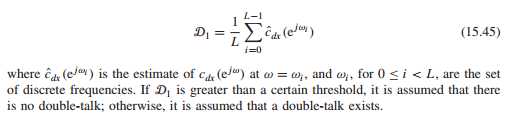
NLP后处理：
----------------------------------------------------------------------------------------------------------------------
子带自适应滤波器的若干问题
子带滤波器要完美重建需要满足一定条件，实际工程中，只需满足现实需求即可。
优点：
1.分成子带后，每个子带的信号变得相对平坦，频谱下采样后，有利于滤波器收敛。
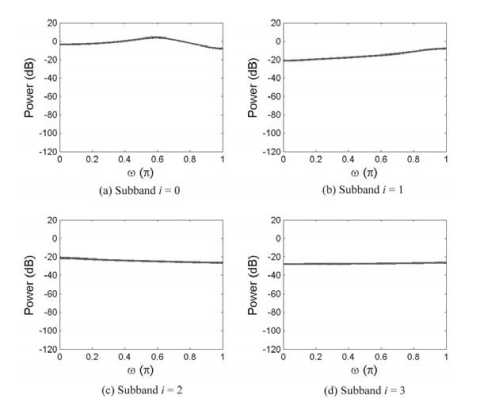
代码中，对子带频域信号进行循环偏移(时域抽取)，只取前面FS/D。
D决定了把频谱分成几个块，把这几个块进行循环右移动0~D-1，叠加在第一个块中。
Hz(i) 送入第几个子带信号，进行下采样(频谱下采样最后得到 W/D带宽的窄带信号)。
子带信号的时域和频域做法
子带时域，每隔D次更新 恢复，先通过FFT变换，变成频域子带信号(已经偏移好了)，之后如频域做法
频域做法就是偏移叠加，取第一个块。 恢复全带过程： 重新组合， 频域全带 Ifft 时域全带
相对于子带，过采样的好处，减少混叠。如果是严格下采样，相邻子带有混叠。
将子带信号进行频谱下采样后，可以重新排列，组合成全带信号。
因为子带 1,2,3 和 子带 7,6,5 共轭对称。所以仅需子带0,1,2,3,4可以恢复出全带信号。(i=1,2,...N/2-1)子带 与 N-i子带共轭对称。
2.分成子带后，滤波器的阶数较低，计算量较小。
3.分成子带后，有利于各个子带的并行处理。
缺点：
下采样会造成各个子带有混叠，而且混叠不可避免。对于单个子带来说，混叠相对于添加了噪声，这个会干扰自适应的过程。
为了减小混叠的影响，可以进行过采样，但是这会造成许多小的特征值(自相关矩阵)，这称为子带边界效应。
过采样的好处：减小混叠，均方误差较小；但是相对于严格下采样，一个快的初始收敛，慢的稳定收敛渐进线(边界效应，小的特征值)，如图：
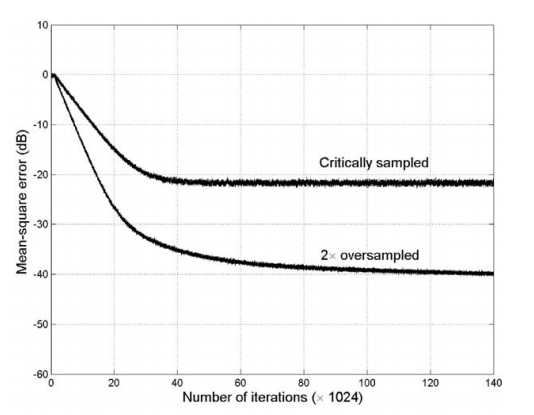
解决的思路：1.融合自适应cross-filter滤波器进行混叠补偿。 2.采用MSAF。 3.采用闭环结构。最小化全局的均方误差，而不是子带。
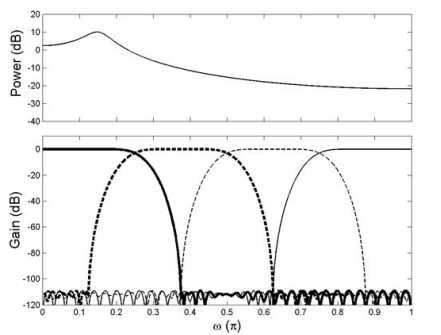
fir1(127,1/4)低通原型滤波器，Hi(z) = 原型滤波器 指数调制，为复数，所以频谱不会对称。
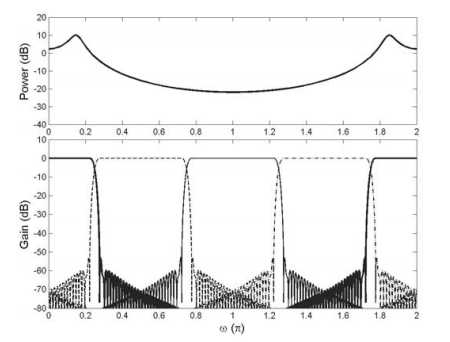
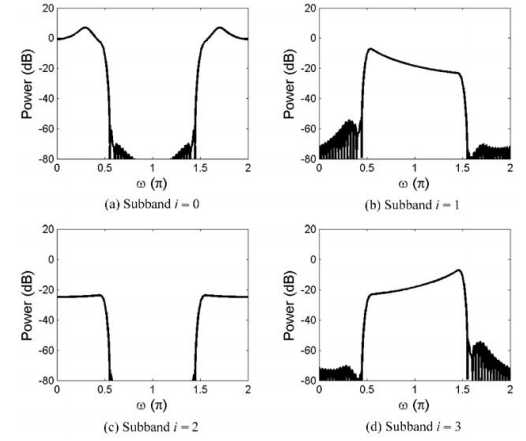
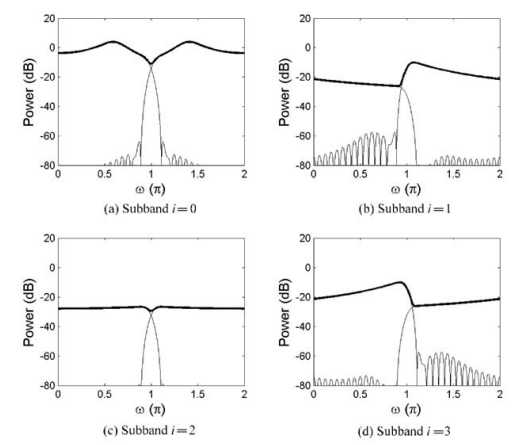
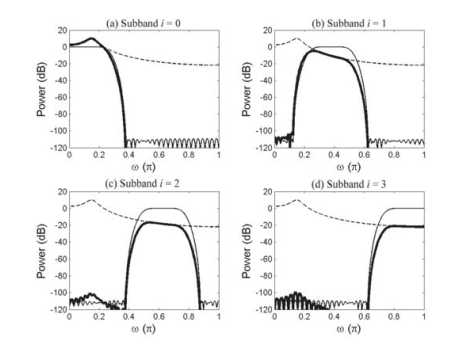
四个子带； 过采样2倍，减小混叠，但是造成小的特征值；严格下采样，还是包含不希望的混叠分量。
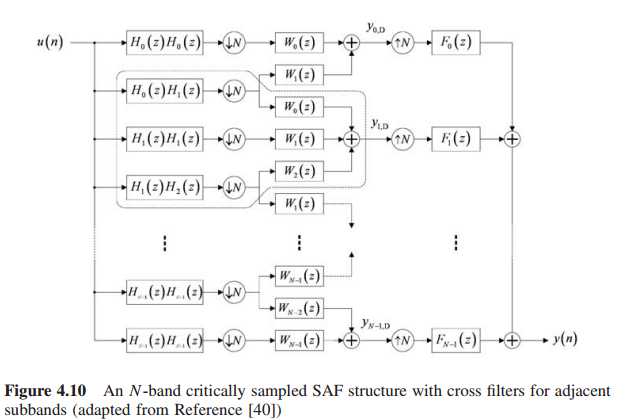
cross-filter，相邻子带之间相互影响的因素考虑进去：如图
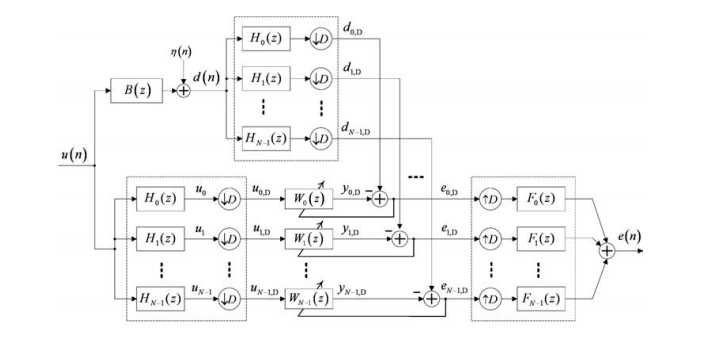
开环结构：
对输入信号和期望信号都进行子带分解，每个子带滤波器都各自独立的进行自适应收敛，它不是全局均方误差最小化，而是
各个子带均分误差之和最小。
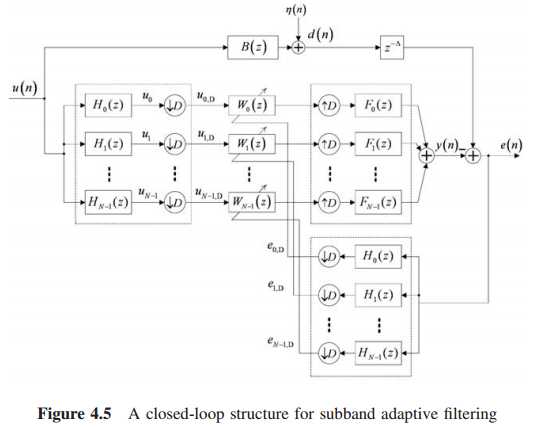
闭环结构：
对输入信号和误差信号进行子带分解，最小化全局整频带的均方误差最小，有利于减小边界效应和混叠效应，合成时有时延对齐。
PNLMS 加快收敛，误差较大
IPNLMS(improved proportionate) 扩展了NLMS算法，使用不同的步长，针对不同的系数，收敛率不依赖于信号的能量强度。
PMSAF 使用一系列子带信号 用全带滤波器
PMSAF在自适应阶段使用子带信号，这是与IPNLMS最主要的区别。
与之相似的是，步长的计算基于每个系数的幅度。
基本思想：刚开始用大步长，后面用小步长。梯度大时，用小步长，梯度小时，用大步长。
BLMS 分块的LMS时域算法
FBLMS 分块的LMS频域实现算法，可能造成大的时延
PFBLMS 分块频域快速块LMS，可以减小时延，处理长时回声
PBFDAF 或者说FBLMS是MDF的特殊情况，h(n)不作分块，或者说分块为1.
又称为MDF, 与FBLMS,不同的是，h(n)也做了分块，分段块频域自适应滤波，处理长时回声，时延小
标签：因子 alt 表示 而且 bfd 变换 误差 均方误差 循环
原文地址：http://www.cnblogs.com/welen/p/6978017.html
