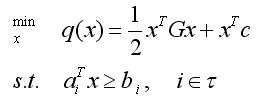标签：参考 定义 目标 最小值 学习 nbsp 变量 .com href
刚开始接触，先看《机器学习》周老师这本书，开始有点乱，最后清楚之后再进行整理
1.拉格朗日乘子（Lagrangemultiplier）
假设需要求极值的目标函数(objectivefunction)为f(x,y)，限制条件为φ(x,y)=M
设 
定义一个新函数 
则用偏导数方法列出方程：
、
、
求出x,y,λ的值，代入即可得到目标函数的极值。
扩展为多个变量的式子为：
F(x1,x2,...,xn,λ)=f(x1,x2,...,xn)-λg(x1,x2,...,xn)
则求极值点的方程为：?F/?xi=0（xi即为x1,x2,...,xn等自变量）?F/?λ=g(x1,x2,...,xn)=0
2.凸二次规划
二次规划的一般形式可以表示为，如右下图：
其中G是Hessian矩阵，τ是有限指标集，c，x和{ai}，都是R中的向量。如果Hessian矩阵是半正定的，则我们说（1.1）是一个凸二次规划，
在这种情况下该问题的困难程度类似于线性规划如果=0，二次规划问题就变成线性规划问题了）。
如果有至少一个向量满足约束并且在可行域有下界，则凸二次规划问题就有一个全局最小值。
如果是正定的，则这类二次规划为严格的凸二次规划，那么全局最小值就是唯一的。如果是一个不定矩阵，则为非凸二次规划，
这类二次规划更有挑战性，因为它们有多个平稳点和局部极小值点。
3.
参考： 百度文库（具体不标注了，都是公式和概念）
《机器学习》周志华老师
支持向量机初探
标签：参考 定义 目标 最小值 学习 nbsp 变量 .com href
原文地址：http://www.cnblogs.com/wjy-lulu/p/6979436.html
