标签:注意 而且 out 最短路径 最小 出错 单源最短路径 -- 时间
上次我们学习了Dijkstra,其有一个不错的时间复杂度上限:O(n log n),但其对于负权边的处理会出错啦
一个简单的小例子:
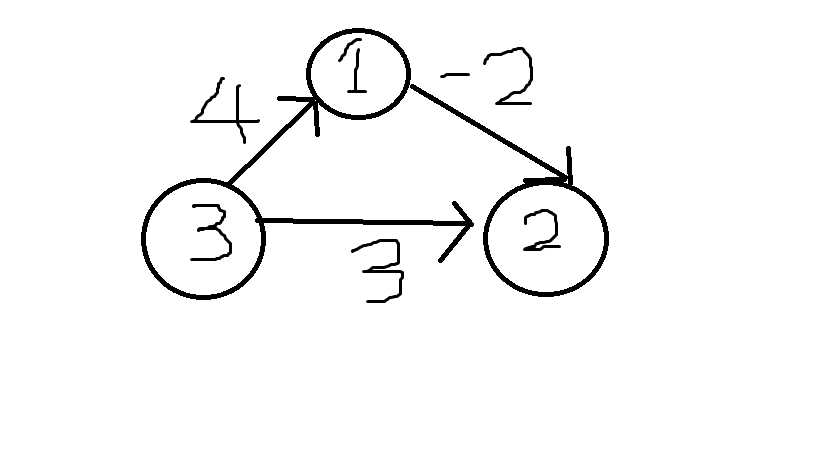
这个图中如果我们发现以3号点为原点,跑一边dijkstra的话
我们先会取2号点进入原点集合,再取一号点。这样得到的dist[2]=3,dist[1]=4
错!
我们很容易发现其实dist[1]=4,dist[2]=2;先取1,再取2。
令人难受接受的是不是我们选取边的方式错了,而是算法本身就有漏洞!
因为上次dijkstra正确性证明时的dist[i]最小,则其则不存在其他店更新i的想法是错的!
这就需要我们寻找一个新的算法
就是bellman了
在这个算法中,我们暴力的把每条边都更新一次,更新|V|-1次,而且如果第|V|次还可以更新的话,就存在负权环了!
百度百科:
所以总的时间复杂度为O(n*m),不算优,但可以优化到SPFA,具高效(貌似还是中国人发明的)
另外,运用bellman-Ford算法还可以解决差分约束图的问题
下一篇文章讨论。
代码:
#include<iostream> #include<cstdio> #include<algorithm> #define INF 100000 const int N=500005; struct note{ int u,v,c; }Edge[N]; int dist[N]; using namespace std; int main() { int n,m,s; scanf("%d %d %d",&n,&m,&s); for(int i=1;i<=m;i++) { scanf("%d %d %d",&Edge[i].u,&Edge[i].v,&Edge[i].c); } for(int i=1;i<=n;i++) dist[i]=INF; dist[s]=0; for(int i=1;i<n;i++) { bool flag=1; for(int j=1;j<=m;j++) if(dist[Edge[j].u]+Edge[j].c<dist[Edge[j].v]) dist[Edge[j].v]=dist[Edge[j].u]+Edge[j].c,flag=0; if (flag) break; } cout<<dist[1]; for(int i=2;i<=n;i++) printf(" %d",dist[i]); cout<<endl; } //若有错误请大佬更正
标签:注意 而且 out 最短路径 最小 出错 单源最短路径 -- 时间
原文地址:http://www.cnblogs.com/dancer16/p/6979631.html