标签:++ main i++ turn width 静态 回归 closed math
下面就让我这个今天上午刚刚MLE的鸡来分析一下。
内存上限就是指程序运行时消耗的内存。
如果你声明的是静态的(数组、普通变量等),那内存计算就是单位数*每个单位所用的字节数之和。(动态的东西,我们这里不做研究)

#define ll long long ll a[400000] ;
我们定义了一个ll类型的a数组。
一个ll占8个字节,那么这个数组就占了400000 * 8 = 3200000B = 3125KB
依次这么算下去,就可以粗略的估计自己占了多少内存了。
那么问题来了,自己的程序要占多少内存才不会MLE呢?
假如程序要求是128M。那么我们大约留出来10到15MB的内存(供代码的字使用吗,再一个可以防止意外得发生),剩下的110多给变量使用就比较稳妥了。
下面给出各种变量占内存多少的数据以及各个单位的换算关系。
数据大小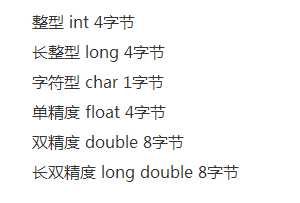 换算关系
换算关系
事实上我们不需要如同上述那样,开到110MB内存的样子。
举个栗子来说吧。

就这个题啊——补天计划。我对这个题很无语的,这个题我就MLE了。
不得不抱怨的是,你会看到这个题根本就没写内存限制是多少。
那么,再来看一下我的代码

1 #include<iostream> 2 #include<cmath> 3 using namespace std; 4 int du[10050] ={0}, ola[10050] ={0}, n , start = 0, 5 map[1050][1050] ={0}, m = 0 , tot = 0; 6 void dfs(int k){ 7 for(int i = 1 ; i <= m ; i++){ 8 if(map[k][i] != 0){ 9 map[k][i] --; 10 map[i][k] --; 11 dfs(i); 12 } 13 } 14 tot++; 15 ola[tot] = k; 16 } 17 18 int main(){ 19 freopen("fence.in" , "r" , stdin); 20 freopen("fence.out" , "w" , stdout); 21 int x , y; 22 cin >> n; 23 for(int i = 1 ; i <= n ; i++){ 24 cin >> x >> y; 25 map[x][y] ++; 26 map[y][x] ++; 27 du[x] ++; 28 du[y] ++; 29 m = max(x , m); 30 m = max(m , y); 31 } 32 for(int i = 1 ; i <= m ; i ++) { 33 if(du[i] % 2 == 1){ 34 start = i; 35 break; 36 } 37 } 38 if(start == 0){ 39 for(int i = 1 ; i <= m ; i ++){ 40 if(du[i] > 0){ 41 start = i; 42 break; 43 } 44 } 45 } 46 dfs(start); 47 for(int i = tot ; i >= 1 ; i--){ 48 if(ola[i] > 500) 49 ola[i] %= 500; 50 cout << ola[i] << endl; 51 } 52 return 0; 53 }
(10050 + 10050 + 1050 * 1050) * 8 = 8980800B = 8770.3125KB ≈ 8.6MB
加上代码什么乱七八糟的能占用15MB不得了了(这么小的内存占用也会爆?)
算了,抱怨先不提,回归正题吧。
定义变量的时候最好能定义 数据范围 的最大值+10到20(防止溢出)这个题我后来改成了定义550*550的二维数组就没有MLE。
另外加一个提示:如果最后两个点数据较大,你没有绝对能做对的方法,而且你还面临着MLE的危险,你到不如就弄到小一点的数据,防止最大化数据结果全部MLE,你内存弄小点得80分和你冒险得0分差别是无限大的。
刚刚有个大佬给出了简便的方法,选中的就是内存大小(B做单位)
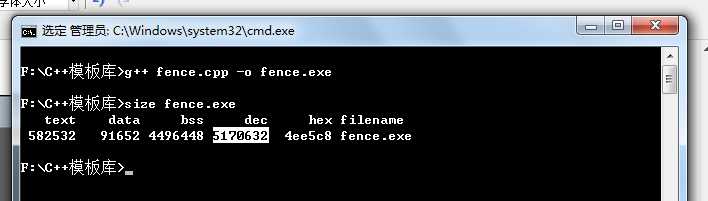
这个使用要有前提的(加一些乱七八糟的东西需要配置好G++才行——方法详见另一篇博客【链】)
以上两种方法都可以算内存,第二种不会就第一种吧(第二种很显然更科学,不会也无所谓),第一个必须要估计的多一些才行。比直接计算的多留出5到10MB就OK了。
总结结束。采用以上两个方法就能大大减小MLE的几率了。
标签:++ main i++ turn width 静态 回归 closed math
原文地址:http://www.cnblogs.com/2464638814-xch/p/6985145.html