标签：lan 处理 blank 矩阵 a10 利用 blog 百度百科 价值
仿射变换（Affine Transformation或 Affine Map），是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。
仿射变换可以由以下基本变换复合而成：平移（Translation）、缩放（Scale）、翻转（Flip）、旋转（Rotation）和错切（Shear），这些基本的变换如下图1表示：
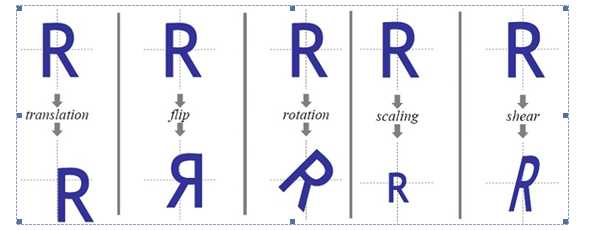
图1
下图2中变换矩阵将原坐标(x, y)变换为新坐标(x‘, y‘)
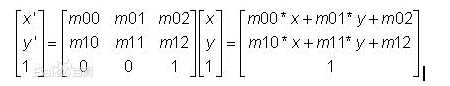
图2
最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。
这是一个示例：某次实验得到了四个数据点 ：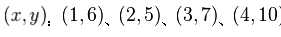
（图3红色的点）。我们希望找出一条和这四个点最匹配的直线
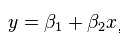，即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的
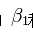和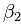 
：
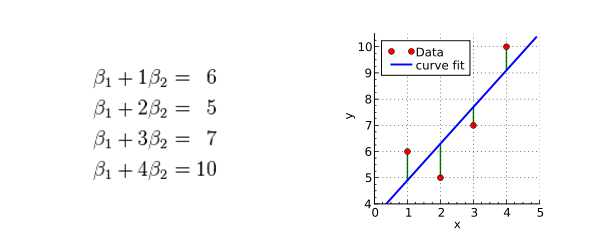
图3
最小二乘法采用的手段是尽量使得等号两边的方差最小，也就是找出这个函数的最小值：
如此就得到了一个只有两个未知数的方程组，很容易就可以解出：
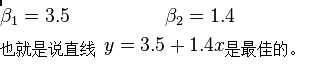
景物在成像过程中产生的扭曲，会使图像的比例失调，可用仿射变换来校正各种畸变。而仿射变换的参数可以用最小二乘法进行估算。
设原图像为f(x,y)，畸变后的图像为F(X‘,Y‘)，要将F(X‘,Y‘)恢复为f(x,y)，就是要找到(X‘,Y‘)坐标与(x,y)坐标的转换关系，这个转换关系称为坐标变换，表示为(x,y)=T(X‘,Y‘)。
景物在成像过程中产生的扭曲，会使图像的比例失调，可用仿射变换来校正各种畸变。先计算出坐标变换的系数，仿射变换的表达式为:R(x)=Px+Q, x=(x,y)是像素的平面位置，P是2*2的旋转矩阵，Q是2*1的平移向量，P、Q即为仿射变换参数，即：
x= AX‘ + BY‘ + C
y= DX‘ + EY‘ + F
因此，几何畸变的校正归根结底为坐标转换系数A,B,C,D,E,F的求解。
为了防止出现空像素，一般采用反向映射，由最小二乘法得(matlab)：
vec1 = inv([X Y I]‘*[X Y I])*[X Y I]‘*U;
vec2 = inv([X Y I]‘*[X Y I])*[X Y I]‘*V;
其中vec1＝[A B C]‘; vec2 =[D E F]‘; X Y U V I分别是x，y，X‘, Y‘, 1构成的向量。
最小二乘法估计就是估计原始坐标点与经过变换后的坐标点之间的关系，从通过这种关系进行矫正图像，大体步骤如下：
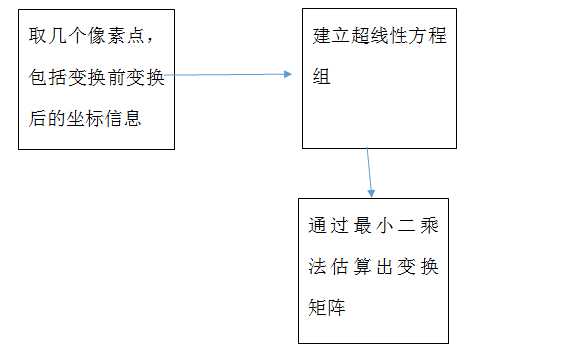
对于处理图形畸变上，最小二乘仿射变换可以通过处理畸变的图形，还原图像原始形状。
另外，在测绘方面，最小二乘与仿射变换有着巨大的应用价值。文献7给出了一种不同坐标系统间转换的方法，在不同的地图坐标系中，使用最小二乘与仿射变换求取变换矩阵，完成坐标系间的转换。文献8则是研究地图数字化扫描的问题，使用最小二乘与仿射变换解决因分辨率、扫描设备带来的地图扫描不精确的问题。
[1] 百度百科.仿射变换. http://baike.baidu.com/view/954621.htm 2013.09.17
[2] wiki百科.仿射变换.http://zh.wikipedia.org/wiki/仿射变换 2014.09.13
[3] ChenLee_1.仿射变换.http://blog.csdn.net/carson2005/article/details/7540936 2012.05.07
[4] wiki百科.最小二乘法. http://zh.wikipedia.org/wiki/最小二乘法 2014.11.11
[5] 百度百科.超定线性. http://baike.baidu.com/view/5113042.htm 2011.01.20
[6] fengbingchun.在图像变换中用最小二乘法求解仿射变换参. http://blog.csdn.net/fengbingchun/article/details/5969193 2010.10.27
[7] 孔建, 姚宜斌, 许双安. 整体最小二乘求取坐标转换参数[J]. 大地测量与地球动力学, 2010, (3).
[8] 岳东杰, 梅红. 地图扫描矢量化误差的最小二乘配置法处理研究[J]. 测绘科学, 2007, (2):51-53.
标签：lan 处理 blank 矩阵 a10 利用 blog 百度百科 价值
原文地址：http://www.cnblogs.com/bingdaocaihong/p/7003581.html
