标签:style blog http color os io for 数据 2014
题目链接:http://poj.org/problem?id=3061
先说说最朴素的算法,那就是for嵌套了,复杂度是O(n^3)太慢,想都不用想一定会超时。接下来有的人可能会想到二分搜索的思想,将时间复杂度优化成O(n*logn),我试了一下,可以AC。
但是这都不是今天要说的重点,今天要说的是一个ACM比赛中常用的技巧方法——尺取法。这是一种可以直接将时间复杂度优化到O(n)的算法。
我们先来介绍一下尺取法。尺取法,顾名思义,像尺子一样,一块一块的截取。是不是解释的有点让人纳闷~。。没关系,下面我们通过这个题目来体会尺取法的魅力。
题目翻译:
给定长度为n的数列整数a0,a1,a2,a3 ..... an-1以及整数S。求出综合不小于S的连续子序列的长度的最小值。如果解不存在,则输出0。
限制条件:
10<n<10^5
0<ai<10^4
S<10^8
这里我们拿第一组测试数据举例子,即 n=10, S = 15, a = {5,1,3,5,10,7,4,9,2,8}
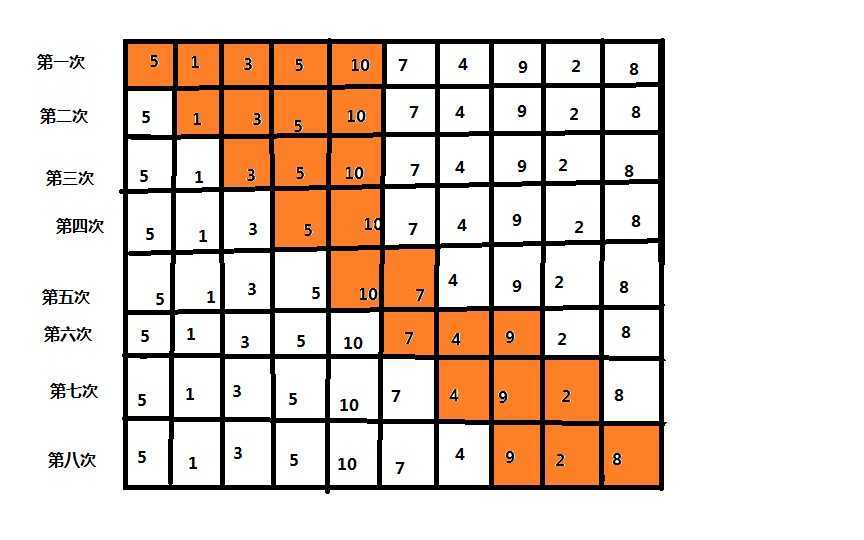
这幅图便是尺取法怎么“取”的过程了。
整个过程分为4布:
1.初始化左右端点
2.不断扩大右端点,直到满足条件
3.如果第二步中无法满足条件,则终止,否则更新结果
4.将左端点扩大1,然后回到第二步
用尺取法来优化,使复杂度降为了O(n)。
最后,再给一个尺取法的定义以便更好理解:返回的推进区间开头和结尾,求满足条件的最小区间的方法称为尺取法。
结尾给大家送上这个题用尺取法的ac代码吧...
#include <iostream> #include <algorithm> using namespace std; int a[100001]; int main() { int x,y; int t; int res; int num; int l,r; int sum; cin>>num; while(num--) { sum = 0; res = 999999999; cin>>x>>y; for(int i=1;i<=x;i++) { cin>>a[i]; } r = 1; l = 1; for(;;) { while(r<=x&&sum<y) { sum += a[r]; r++; } if(sum<y) break; res = min(res,r-l); sum -= a[l]; l++; } if(res==999999999) res = 0; cout<<res<<endl; } return 0; }
从具体题目来谈尺取法 POJ 3061 Subsequence
标签:style blog http color os io for 数据 2014
原文地址:http://www.cnblogs.com/ltwy/p/3944685.html