标签:special inpu 第一个 blog 向量 uniq planet another output
题目链接:
http://poj.org/problem?id=1696
题目描述:
Description
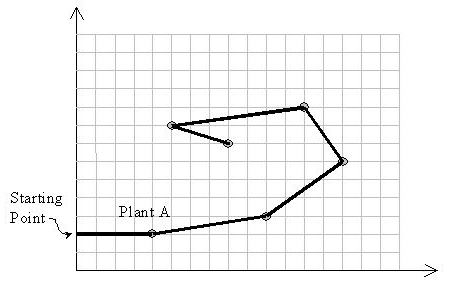
Input
Output
Sample Input
2 10 1 4 5 2 9 8 3 5 9 4 1 7 5 3 2 6 6 3 7 10 10 8 8 1 9 2 4 10 7 6 14 1 6 11 2 11 9 3 8 7 4 12 8 5 9 20 6 3 2 7 1 6 8 2 13 9 15 1 10 14 17 11 13 19 12 5 18 13 7 3 14 10 16
Sample Output
10 8 7 3 4 9 5 6 2 1 10 14 9 10 11 5 12 8 7 6 13 4 14 1 3 2
题目大意:
一只生物吃东西……它不能右转,走路会留下痕迹,且不能穿过之前走过的痕迹
现在有这么多食物,要从y轴上与你第一个到达的点的投影出发,问最多可以吃几个食物
思路:
想象生物面朝的方向延伸出一条射线,射线顺时针方向的所有区域和路径的相交为你剩下可以吃到的区域(搜索区域)
所以每次转向都在缩小你的搜索区域,转得角度越大,缩小得越厉害
贪心的思想,每次选择剩下可以走的点(注意判断之前线段都不想交)中,转角最小的那个点,这样会保证搜索区域尽可能的大
起始点选择最下面的点,因为假设选择不是最下面的点,总存在点(起始点之下)永远不在你的搜索区域中
代码:
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 #include <cmath> 6 using namespace std; 7 8 const double EPS = 1e-10; //精度系数 9 const int INF = 0x3f3f3f3f; 10 const double PI = acos(-1.0); 11 const int N = 55; 12 13 struct Point { 14 double x, y; 15 Point(double x = 0, double y = 0) :x(x), y(y) {} 16 }; //点的定义 17 18 typedef Point Vector; //向量的定义 19 20 Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); } //向量减法 21 22 int dcmp(double x) { 23 if (fabs(x) < EPS)return 0; else return x < 0 ? -1 : 1; 24 } //与0的关系 25 26 double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; } //向量叉乘 27 double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; } //向量点乘 28 double Length(Vector A) { return sqrt(Dot(A, A)); } //向量长度 29 30 double Angle(Vector A, Vector B) { 31 double ans = atan2(A.y, A.x) - atan2(B.y, B.x); 32 return ans + (ans < 0 ? 2 * PI : 0); 33 } //向量夹角( 范围[0, 2π) ) 34 35 bool SegmentProperIntersection(Point& a1, Point& a2, Point& b1, Point& b2) { 36 double c1 = Cross(a2 - a1, b1 - a1), c2 = Cross(a2 - a1, b2 - a1), 37 c3 = Cross(b2 - b1, a1 - b1), c4 = Cross(b2 - b1, a2 - b1); 38 return dcmp(c1)*dcmp(c2) < 0 && dcmp(c3)*dcmp(c4) < 0; 39 } //判断两线段相交(恰有一个公共点且不在端点) 40 41 bool OnSegment(Point& p, Point& a1, Point& a2) { 42 return dcmp(Cross(a1 - p, a2 - p)) == 0 && dcmp(Dot(a1 - p, a2 - p)) < 0; 43 } //判断点是否在一条线段上(不含端点) 44 45 int n, index[N], best, ans[N], res[N]; 46 Point P[N]; 47 bool vis[N]; 48 49 bool ok(int cur, int next, int now) { 50 Point last(0, P[res[0]].y); 51 for (int i = 0; i < cur; ++i) { 52 if (SegmentProperIntersection(last, P[res[i]], P[now], P[next]) 53 || OnSegment(P[res[i]], P[now], P[next]))return false; 54 last = P[res[i]]; 55 } 56 return true; 57 } 58 59 void solve(int cur, int id, Vector v) { 60 double MIN = INF, L = INF; 61 int next = 0; 62 for (int i = 1; i <= n; ++i)if (!vis[i]) { //如果没有访问过 63 double agl = Angle(P[i] - P[id], v); //夹角 64 if (agl >= PI || !ok(cur, i, id))continue; //保证方向,且与之前线段不相交 65 if (agl < MIN || (dcmp(agl - MIN) == 0 && Length(P[i] - P[id]) < L)) //扫描夹角最小的 66 MIN = agl, next = i, L = Length(P[i] - P[id]); 67 } 68 if (next) { 69 vis[next] = true; 70 res[cur] = next; 71 solve(cur + 1, next, P[next] - P[id]); 72 vis[next] = false; 73 } else if (cur > best) { //不能再继续 74 best = cur; 75 memcpy(ans, res, sizeof(ans)); 76 } 77 } 78 79 int main() { 80 int t; 81 cin >> t; 82 while (t--) { 83 memset(vis, 0, sizeof(vis)); 84 best = 0; 85 cin >> n; 86 double tmp = INF; 87 int m; 88 for (int i = 1; i <= n; ++i) { 89 scanf("%d%lf%lf", &index[i], &P[i].x, &P[i].y); 90 if (P[i].y < tmp) { tmp = P[i].y, m = i; } //找到y坐标最小的点 91 } 92 vis[m] = true; 93 res[0] = m; 94 solve(1, m, Vector(P[m].x, 0)); 95 printf("%d", best); 96 for (int i = 0; i < best; ++i)printf(" %d", index[ans[i]]); 97 printf("\n"); 98 } 99 }
POJ1696 Space Ant(贪心、向量叉乘、向量极角、线段相交、点在线段上)
标签:special inpu 第一个 blog 向量 uniq planet another output
原文地址:http://www.cnblogs.com/hyp1231/p/7017683.html