标签:描述 mod logs oss struct ret UI span 操作
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
输入格式:
第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含N个非负整数,分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通)
接下来M行每行包含若干个正整数,每行表示一个操作,格式如下:
操作1: 1 x y z
操作2: 2 x y
操作3: 3 x z
操作4: 4 x
输出格式:
输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)
5 5 2 24 7 3 7 8 0 1 2 1 5 3 1 4 1 3 4 2 3 2 2 4 5 1 5 1 3 2 1 3
2 21
时空限制:1s,128M
数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=1000,M<=1000
对于100%的数据:N<=100000,M<=100000
(其实,纯随机生成的树LCA+暴力是能过的,可是,你觉得可能是纯随机的么233)
样例说明:
树的结构如下:
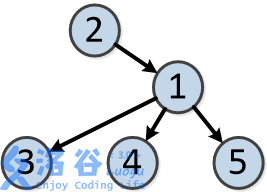
各个操作如下:
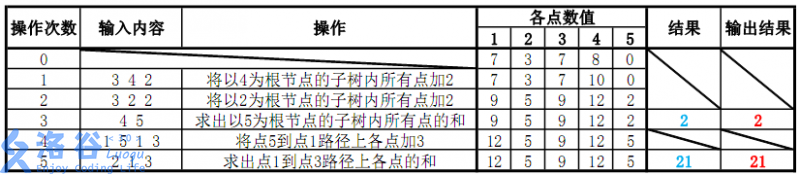
故输出应依次为2、21(重要的事情说三遍:记得取模)
1 #include <algorithm> 2 #include <cstdio> 3 4 using namespace std; 5 6 const int N(100000+15); 7 const int M(200000+15); 8 int n,m,rt,mod,u,v,w,op,val[N]; 9 10 int head[N],sumedge; 11 struct Edge 12 { 13 int u,v,next; 14 Edge(int u=0,int v=0,int next=0): 15 u(u),v(v),next(next){} 16 }edge[M<<1]; 17 void ins(int u,int v) 18 { 19 edge[++sumedge]=Edge(u,v,head[u]); 20 head[u]=sumedge; 21 } 22 23 int deep[N],dad[N],son[N],size[N],top[N],dfn[N],id[N],cnt; 24 /*void DFS(int u,int father,int deepth) 25 { 26 deep[u]=deepth; 27 dad[u]=father; 28 size[u]=1; 29 son[u]=0; 30 for(int i=head[u];i;i=edge[i].next) 31 { 32 int to=edge[i].v; 33 if(dad[u]==to) continue; 34 DFS(to,u,deepth+1); size[u]+=size[to]; 35 if(!son[u]||size[son[u]]<size[to]) son[u]=to; 36 } 37 } 38 void DFS_(int u,int Top) 39 { 40 top[u]=Top; 41 id[u]=++cnt; 42 dfn[cnt]=u; 43 if(son[u]) DFS_(son[u],Top); 44 for(int i=head[u];i;i=edge[i].next) 45 { 46 int to=edge[i].v; 47 if(to!=dad[u]&&to!=son[u]) DFS_(to,to); 48 } 49 }*/ 50 void DFS(int x) 51 { 52 size[x]=1;deep[x]=deep[dad[x]]+1; 53 for(int i=head[x];i;i=edge[i].next) 54 { 55 int to=edge[i].v; 56 if(dad[x]!=to) 57 { 58 dad[to]=x; 59 DFS(to); 60 size[x]+=size[to]; 61 } 62 } 63 } 64 void DFS_(int x) 65 { 66 id[x]=++cnt;dfn[cnt]=x; 67 int t=0;if(!top[x]) top[x]=x; 68 for(int i=head[x];i;i=edge[i].next) 69 { 70 int to=edge[i].v; 71 if(dad[x]!=to&&size[t]<size[to]) t=to; 72 } 73 if(t) top[t]=top[x],DFS_(t); 74 for(int i=head[x];i;i=edge[i].next) 75 { 76 int to=edge[i].v; 77 if(dad[x]!=to&&t!=to) DFS_(to); 78 } 79 } 80 81 struct Tree 82 { 83 int l,r,flag,val,mid; 84 }tree[M<<2]; 85 void Tree_up(int now) 86 { 87 tree[now].val=tree[now<<1].val+tree[now<<1|1].val; 88 } 89 void Tree_down(int now) 90 { 91 tree[now<<1].flag+=tree[now].flag; 92 tree[now<<1].val=(tree[now<<1].val+(tree[now].mid-tree[now].l+1)*tree[now].flag)%mod; 93 tree[now<<1|1].flag+=tree[now].flag; 94 tree[now<<1|1].val=(tree[now<<1|1].val+(tree[now].r-tree[now].mid)*tree[now].flag)%mod; 95 tree[now].flag=0; 96 } 97 void Tree_build(int now,int l,int r) 98 { 99 tree[now].l=l,tree[now].r=r; 100 if(l==r) 101 { 102 tree[now].val=val[dfn[l]]; 103 return ; 104 } 105 tree[now].mid=tree[now].l+tree[now].r>>1; 106 Tree_build(now<<1,l,tree[now].mid); 107 Tree_build(now<<1|1,tree[now].mid+1,r); 108 Tree_up(now); 109 } 110 void Tree_change(int now,int l,int r,int x) 111 { 112 if(tree[now].l==l&&tree[now].r==r) 113 { 114 tree[now].flag+=x; 115 tree[now].val=(tree[now].val+(tree[now].r-tree[now].l+1)*x)%mod; 116 return ; 117 } 118 if(tree[now].flag) Tree_down(now); 119 if(tree[now].mid>=r) Tree_change(now<<1,l,r,x); 120 else if(tree[now].mid<l) Tree_change(now<<1|1,l,r,x); 121 else 122 { 123 Tree_change(now<<1,l,tree[now].mid,x); 124 Tree_change(now<<1|1,tree[now].mid+1,r,x); 125 } 126 Tree_up(now); 127 } 128 int Tree_query(int now,int l,int r) 129 { 130 if(tree[now].flag) Tree_down(now); 131 if(tree[now].l==l&&tree[now].r==r) 132 return tree[now].val%mod; 133 if(tree[now].mid>=r) return Tree_query(now<<1,l,r); 134 else if(tree[now].mid<l) return Tree_query(now<<1|1,l,r); 135 else return (Tree_query(now<<1,l,tree[now].mid)+Tree_query(now<<1|1,tree[now].mid+1,r))%mod; 136 } 137 138 void List_change(int x,int y,int z) 139 { 140 for(;top[x]!=top[y];x=dad[top[x]]) 141 { 142 if(deep[top[x]]<deep[top[y]]) swap(x,y); 143 Tree_change(1,id[top[x]],id[x],z); 144 } 145 if(deep[x]<deep[y]) swap(x,y); 146 Tree_change(1,id[y],id[x],z); 147 } 148 int List_query(int x,int y) 149 { 150 int ret=0; 151 for(;top[x]!=top[y];x=dad[top[x]]) 152 { 153 if(deep[top[x]]<deep[top[y]]) swap(x,y); 154 ret=(ret+Tree_query(1,id[top[x]],id[x]))%mod; 155 } 156 if(deep[x]<deep[y]) swap(x,y); 157 ret=(ret+Tree_query(1,id[y],id[x]))%mod; 158 return ret; 159 } 160 161 int main() 162 { 163 scanf("%d%d%d%d",&n,&m,&rt,&mod); 164 for(int i=1;i<=n;i++) scanf("%d",val+i); 165 for(int i=1;i<n;i++) 166 scanf("%d%d",&u,&v),ins(u,v),ins(v,u); 167 DFS(rt); DFS_(rt); 168 // DFS(rt,0,1);DFS_(rt,rt); 169 Tree_build(1,1,n); 170 for(;m--;) 171 { 172 scanf("%d",&op); 173 if(op==1) 174 { 175 scanf("%d%d%d",&u,&v,&w); 176 List_change(u,v,w); 177 } 178 else if(op==2) 179 { 180 scanf("%d%d",&u,&v); 181 printf("%d\n",List_query(u,v)); 182 } 183 else if(op==3) 184 { 185 scanf("%d%d",&u,&w); 186 Tree_change(1,id[u],id[u]+size[u]-1,w); 187 } 188 else 189 { 190 scanf("%d",&u); 191 printf("%d\n",Tree_query(1,id[u],id[u]+size[u]-1)); 192 } 193 } 194 return 0; 195 }
标签:描述 mod logs oss struct ret UI span 操作
原文地址:http://www.cnblogs.com/Shy-key/p/7041230.html