标签:for 数据 const 方案 状态转移方程 std algorithm 入队 span
大致题意:
要打印一长串词语,每个词语有一个对应的打印费用Ci,要给词语分行,一行的总费用记为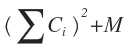 ,M是给定的常数
,M是给定的常数
要求计算一种分行方案使得总费用最小。
数据规模50万。
分析:首先可以想到枚举上一次断行处,这样可以得到最初的状态转移方程: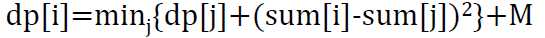
,复杂度为O(n^2)。
观察一下数据规模为50万,需要优化。
主要思路是考虑淘汰肯定对最优答案没有贡献的点。
将状态转移方程展开:
(注:公式和图来自BIG YAO学长)
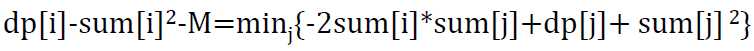
移项可得:
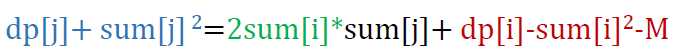
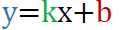
观察到蓝色字体部分只与j有关,绿色字体对给定的i为常量,红色字体部分取最小的时候dp[i]取最小。
将蓝色字体视为y(j),sum[j]视为x(j),问题就转化为对平面上无数个点(x,y),对每一个i,找出一个最优点(x0,y0),使得一条通过该点,斜率为k=2sum[i]的直线的截距最小。
放张图表现一下优化情况:
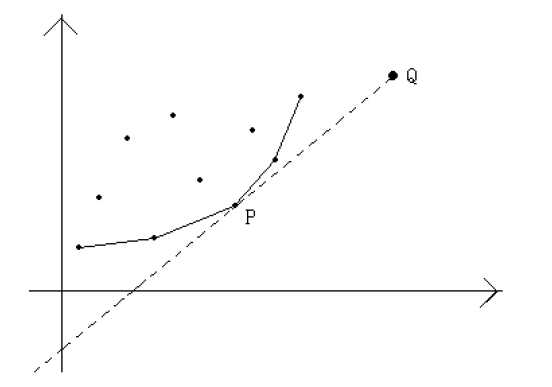
维护一个队列,即为下凸折线上点的队列,每次寻找最优的j的时候只在队列里的点找。(注意取得最优点的时候相邻的两根折线的斜率对于k=2sum[i]一大一小)
以下具体讨论怎么实现:
i不断向前推进,每次循环做两件事情:
1,找出对于dp[i]最优的上一个断行处j
如果队列上该点i和他后面的那个店形成的斜率小于k=2*sum[i]就头指针+1。
注意由于随i的递增,k=2*sum[i]必然递增,所以出队的点就不需要回来了
2,把i放入队列后就不再需要的点淘汰掉:
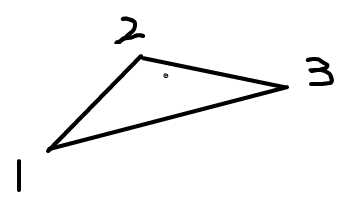
一旦出现3个点呈这样,即可淘汰点2,因为:直线经过点4的截距必然小于经过点2的截距,而经过点4的截距必然小于经过点1或点3的截距。
从而经过点2的截距必然小于小1或点3的截距,点2不可能为最优点,可淘汰。
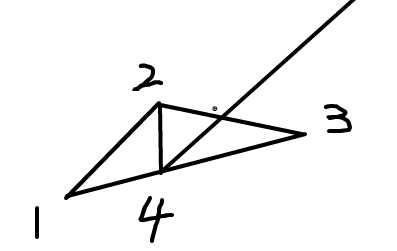
然后把i放入队列(注意sum[i]为严格递增的,所以i个点中最后一个点必然在“外围”,不会被淘汰)
1 #include<cstdio> 2 #include<algorithm> 3 #define rep(i,a,b) for(int i=a;i<=b;++i) 4 using namespace std; 5 const int MAXN=500010; 6 long long int dp[MAXN],q[MAXN],sum[MAXN]; 7 int n,m; 8 inline long long int getdp(int i,int j) 9 { 10 return dp[j]+m+(sum[i]-sum[j])*(sum[i]-sum[j]); 11 } 12 inline long long int gety(int x,int y) 13 { 14 return dp[x]+sum[x]*sum[x]-dp[y]-sum[y]*sum[y]; 15 } 16 inline long long int getx(int x,int y) 17 { 18 return 2*sum[x]-2*sum[y]; 19 } 20 int main() 21 { 22 // freopen("in.txt","r",stdin); 23 while(scanf("%d%d",&n,&m)==2) 24 { 25 sum[0]=0; 26 rep(i,1,n) 27 { 28 scanf("%lld",&sum[i]); 29 sum[i]=sum[i-1]+sum[i]; 30 } 31 dp[0]=0; 32 int head,tail; 33 tail=0; 34 head=0; 35 q[tail]=0; //虚拟制造一个点0,若0点最优代表把所有词语分成一行最优 36 rep(i,1,n) 37 { 38 while(head+1<=tail&&(gety(q[head+1],q[head])<=sum[i]*getx(q[head+1],q[head]))) head++; //寻找对于i最好的上一次分行的截止点 39 dp[i]=getdp(i,q[head]); 40 while(head+1<=tail&&gety(i,q[tail])*getx(q[tail],q[tail-1])<=gety(q[tail],q[tail-1])*getx(i,q[tail])) tail--; //i放入队列后需要淘汰的点 41 q[++tail]=i; //把i放入队列 42 } 43 printf("%lld\n",dp[n]); 44 } 45 return 0; 46 }
标签:for 数据 const 方案 状态转移方程 std algorithm 入队 span
原文地址:http://www.cnblogs.com/zhixingr/p/7045214.html