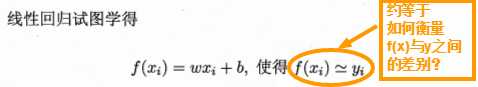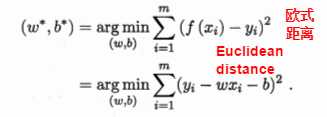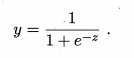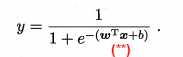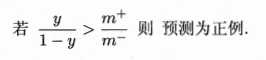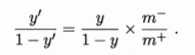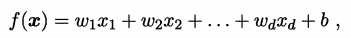
一般用向量形式写成
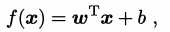
,其中
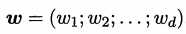
w 和 b 学得之后, 模型就得以确定。
3.2 线性回归
对离散属性的处理:
- 若属性值间存在序关系,可通过连续化将其转化为连续值,例如二值属性“身高”的取值“高”“矮”可转化为 {1.0, 0.0};
- 若属性值间不存在序关系,假定有 k 个属性值,则通常转化为 k 维向量。
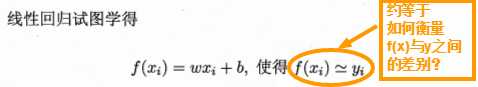
均方差误差最小
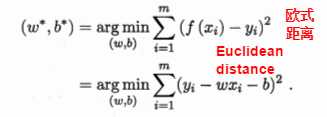
基于均方误差最小化来进行模型求解的方法称为最小二乘法(least square method)。
线性回归模型的最小二乘参数估计:指求解 w 和 b 使 E(w, b) = ∑(yi - wxi - b)2 最小化的过程。
对数线性回归(log-linear regression):
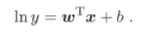
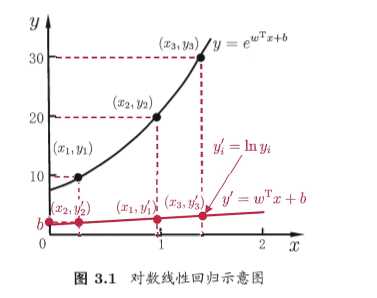
广义线性模型:考虑单调可微函数g,令
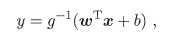
这样得到的模型称为广义线性模型(generalized linear model),函数 g 称为联系函数(link function)。
3.3 对数几率回归
分类任务如何处理?
对数几率函数(logistic function):
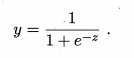
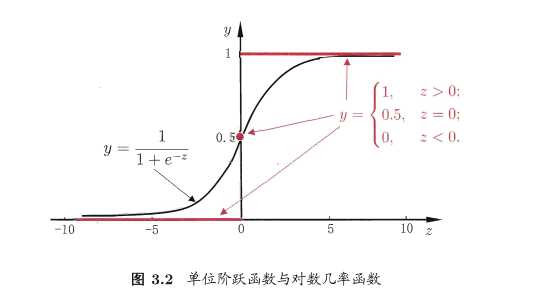
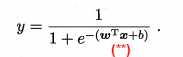
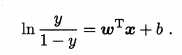
几率:若将 y 看做样本 x 为正例的可能性,则 1-y 为样本 x 为反例的可能性,这两者的比例称为几率。
对数几率:将上述几率取对数。
对数几率回归:(**)式实际上是用线性回归模型的预测结果去逼近真实标记的对数几率,因此,其对应的模型称为对数几率回归(logistic regression)。
它是一种分类学习方法。
对数几率回归的优点:
- 它直接对分类可能性进行建模,无需事先假设数据分布,避免了假设分布不准确所带来的问题。
- 它不仅预测出类别,还得到近似概率预测,对许多需利用概率辅助决策的任务很有用。
- 对率函数是任意阶可导的凸函数,有很好的数学性质,现有的许多数值优化算法都可直接用于求取最优解。
如何确定(**)式中的 w 和 b?
3.4 线性判别分析
线性判别分析(Linear Discriminant Analysis,简称LDA)的思想:
给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影尽可能接近,异类样例的投影尽可能远离。在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来去顶新样本的类别。
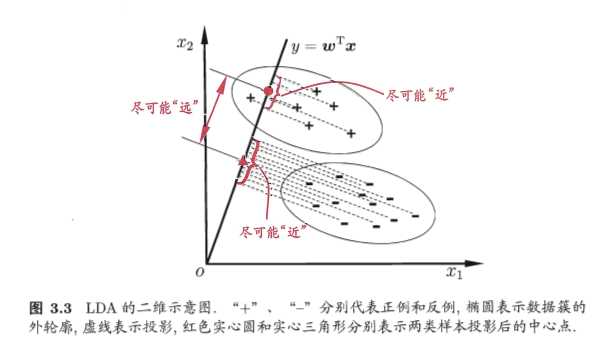
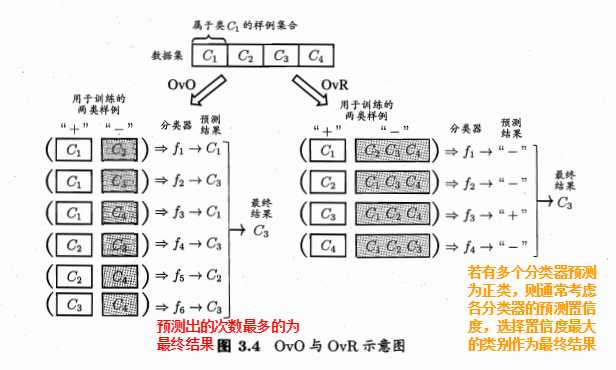
3.5 多分类问题
多分类问题的基本思路是拆解法,即将多分类的任务拆为若干个二分类任务求解。
最经典的拆分策略有三种:一对一(One vs. One,简称OvO),一对其余(One vs. Rest,简称OvR)和多对多(Many vs. Many,简称MvM)。
考虑 N 个类别C1,C2,...,CN,
给定数据集 D = {(x1,y1),(x2,y2),...,(xm,ym)}, yi ∈ {C1,C2,...,CN}
OvO将这 N 个类别两两配对,从而产生 N(N-1)/2 个二分类任务。
OvR是每次将一个类的样例作为正例、所有其他类的样例作为反例来训练 N 个分类器。
MvM是每次将若干个类作为正类,若干个其他类作为反类。MvM的正、反类构造必须有特殊的设计,不能随意选取。最常见的MvM技术为纠错输出码(Error Correcting Output Codes, 简称ECOC)。


纠错:在测试阶段,ECOC编码对分类的错误有一定的容忍和修正能力。
- 一般来说,对同一个学习任务,ECOC编码越长,纠错能力越强。
- 对同等长度的编码,理论上来说,任意两个类别之间的编码距离越远,则纠错能力越强。
3.6 类别不平衡问题
前面几个分类学习方法都有一个共同的假设:不同类别的训练样例数目相同。
类别不平衡(class-imbalance):指分类任务中不同类别的训练样例数目差别很大的情况。
以线性分类器为例,在用 y = wTx + b对新样本 x 进行分类时,实际上是在用预测出的 y 值与一个阈值进行比较,大于阈值时为正例,反之则为反例。
1. 正、反例数目相同时的阈值是0.5,即

2. 正、反例数目不同时的阈值是 m+ / (m+ + m-),即
m+ 表示正例数目,m- 表示返利数目。
这就是类别不平衡学习的一个基本策略——再缩放(rescaling)。
当“训练集是真实样本总体的无偏采样”这个假设不成立时,有以下方法:
| 方法 | 欠采样(undersampling) | 过采样(oversampling) | 阈值移动(threshold-moving) |
| 详情 | 去除一些反例使得正、反例数目接近,然后进行学习 | 增加一些正例使得正、反例数目接近,然后再进行学习 | 直接基于原始训练集进行学习,但在用训练好的分类器进行预测时,将再缩放的公式嵌入到决策过程中 |
| 注 | 1. 时间开销较小
2. 不能随机丢弃反例,可能丢失重要信息。
3. 代表算法EasyEnsemble | 1.不能简单的对初始正例样本进行重复采样,否则会招致严重的过拟合。
2. 代表算法SMOTE | 再缩放也是代价敏感学习的基础。 |