标签:name 如图所示 告诉 正整数 输入输出 包含 printf fine cst
有n个同学(编号为1到n)正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象,其中,编号为i的同学的信息传递对象是编号为Ti同学。
游戏开始时,每人都只知道自己的生日。之后每一轮中,所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象(注意:可能有人可以从若干人那里获取信息,但是每人只会把信息告诉一个人,即自己的信息传递对象)。当有人从别人口中得知自己的生日时,游戏结束。请问该游戏一共可以进行几轮?
输入格式:
输入共2行。
第1行包含1个正整数n表示n个人。
第2行包含n个用空格隔开的正整数T1,T2,……,Tn其中第i个整数Ti示编号为i
的同学的信息传递对象是编号为Ti的同学,Ti≤n且Ti≠i
数据保证游戏一定会结束。
输出格式:
输出共 1 行,包含 1 个整数,表示游戏一共可以进行多少轮。
5 2 4 2 3 1
3
样例1解释
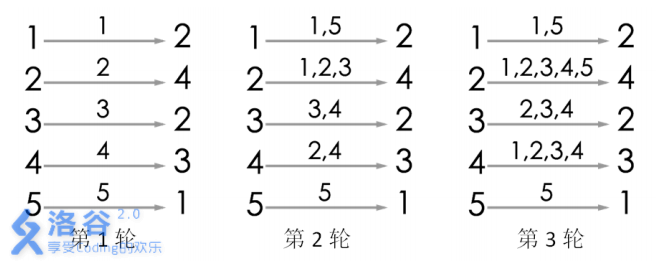
游戏的流程如图所示。当进行完第 3 轮游戏后, 4 号玩家会听到 2 号玩家告诉他自
己的生日,所以答案为 3。当然,第 3 轮游戏后, 2 号玩家、 3 号玩家都能从自己的消息
来源得知自己的生日,同样符合游戏结束的条件。
对于 30%的数据, n ≤ 200;
对于 60%的数据, n ≤ 2500;
对于 100%的数据, n ≤ 200000。
思路:
这道题我们可以分析出这个图的一些特性。
把每个人说话的对象作为这个人连出去的边。那么,我们得到一个N个点N条边的图。并且每个点只有一个出边。
因此,图必然是许多个类似的连通块,而每个连通块都是一棵树加一条边,这条边与原本的树边形成一个环。
实际上我们只需要找出最小环就可以了。
(差不多是一个板子题。。。。)
代码:
#include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> #define N 200010 using namespace std; bool vis[N]; int n,a,tot,top,ans,tim,minn=10000000000; int dfn[N],low[N],head[N],stack[N]; int read() { int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘) f=-1; ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } struct Edge { int from,to,next; }edge[N<<1]; void add(int x,int y) { tot++; edge[tot].to=y; edge[tot].next=head[x]; head[x]=tot; } void tarjan(int now) { dfn[now]=low[now]=++tim; stack[++top]=now; vis[now]=true; for(int i=head[now];i;i=edge[i].next) { int t=edge[i].to; if(vis[t]) low[now]=min(low[now],dfn[t]); else if(!dfn[t]) tarjan(t),low[now]=min(low[t],low[now]); } ans=0; if(low[now]==dfn[now]) { ans++; for(;stack[top]!=now;top--) { ans++; vis[stack[top]]=false; } vis[now]=false; top--; if(ans>1) minn=min(ans,minn); } } int main() { n=read(); for(int i=1;i<=n;i++) a=read(),add(i,a); for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i); printf("%d",minn); return 0; }
错误点:
1.ans别忘了清零,统计每个强连通分量内元素的个数
2.题目中给出要求:ans必须大于0!!(他不能一个人在那绕着玩。。。)
标签:name 如图所示 告诉 正整数 输入输出 包含 printf fine cst
原文地址:http://www.cnblogs.com/z360/p/7056135.html