标签:等于 arrays .com 取模运算 题目 利用 [1] blog 代码
题目要求我们用一个32位整数整除另外一个整数,但是不允许我们使用除法,乘法和取模运算。
有趣的问题,下面说一下我的思路:
首先,先给出两个正整数除法运算的过程。假设a为被除数,而b为除数。在计算机中无符号整数除法div可以用下面的数学公式来表示:
![]()
即计算机除法中的a/b实际上是数学意义上a/b代表的有理数向下取整值。可以换一个方法来等价表示上面公式:
![]()
因此我们只需要能找到一个值c,满足下面条件即可:
![]()
但是我们不能从1到正无穷枚举c,因为如果a足够大且b足够小,那么c的值可能要上亿,上亿次的枚举消耗的时间非常可怕。但是我们不能使用乘法又该如何快速增大枚举值呢。这源于一个思路,v[0]=1,v[1]=v[0]+v[0],...,v[n]=v[n-1]+v[n-1]。发现了吗,v[i]=2^i,而32位整数绝对不会超过v[32],因此我们可以快速的利用v数组快速逼近c。
实际做法如下:
v and u are arrays with size 32
v[0] = 1, u[0] = b
limit = 0
for(; u[limit] < a; limit = limit + 1)
u[limit + 1] = u[limit ] + u[limit ]
v[limit + 1] = v[limit] + v[limit]
这样我们就得到一个数组u,并且保证了u[0], ..., u[limit - 1] < a,且u[limit] >= a,实际上u[i] = b * 2^i。但是我们又该如何能够借助这样一个数组u计算出最终的c?
由于每个整数在计算机中都是由二进制表示而成,因此c必然等于2^i1+2^i2+...+2^in,其中i1,...in互不相同并按增序排序。因此我们所要找的实际上是这样一组i1,i2,...,in。由于2^n=1+2^0+2^1+2^2+...+2^(n-1),因此我们能得知2^in>2^i1+2^i2+...+2^in-1,换句话说有2^in<=c<2^(in+1),等价的形式为u[in]=b*2^in<=b*c=a<b*2^(in+1)=u[in+1]。到了这一步我们就知道如何快速地决定in,而对于in-1的计算,可以通过u[in-1]=b*2^in-1<=b*(c-2^in)=a-u[in]<b*2^(in-1+1)=u[in-1+1]得出,推理过程如上。这样不断地计算下去,我们就可以将i1,i2,...,in全部计算出来。
用代码展示上面的结论:
r = a, c = 0
for(i = limit; r >= b; i--)
if(u[i] <= r)
r = r - u[i]
c = c + v[i]
综合上面我们已经得到了计算两个正整数的方式。上面这个算法的时间复杂度与空间复杂度均为常数O(1),因为不存在与输入相关联的冗余循环。
对于a,b均为负数的除法,有a/b=(-a)/(-b),因此可以直接用上述正整数除法的运算方式。对于a为负数的运算,由于计算机中对于带一个负数除法ndiv的定义如下:
![]()
但是我们不希望为带负数的重新定义一个新的算法,因此利用下面的公式可以推出利用正整数除法div计算的c的方式:
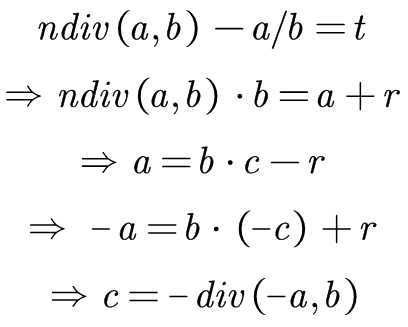
故到了这里问题全面解决。当然这只是理论上的,实践上还会存在数值超出32位整数表示范围的情况,这需要读者自己对特殊情况进行处理。
标签:等于 arrays .com 取模运算 题目 利用 [1] blog 代码
原文地址:http://www.cnblogs.com/dalt/p/7061508.html