标签:std 返回 主函数 visit 哪些 深度优先遍历 efi ring include
一个离散数学的实验:已知一个无向图,求出这个无向图的割边/桥,所有的边割集。
这是初始的定义和头文件
#include <stdio.h> #include <string.h> #include<malloc.h> #define INFINITY 100 #define MAX_VERTEX_NUM 20 typedef int Status; typedef int VRType; typedef char VertexType; typedef char InfoType;
结构体定义
typedef struct ArcCell{ VRType adj;//用1表示相邻,0表示不相邻 }ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; typedef struct{ VertexType vexs[MAX_VERTEX_NUM];//字符顶点 AdjMatrix arcs;//邻接矩阵 int vexnum,arcnum;//图的顶点数和边数 }MGraph;
无向图的构建
int LocateVex(MGraph G,VertexType v) //v在图数组的下标位置 { int i,loc=-1; for(i=0;i<G.vexnum;i++){ if(G.vexs[i] == v){ loc=i; break; } } return loc; }
Status CreateG(MGraph &G)//创建无向图 { int i,j; VertexType x,y; int loc1,loc2; printf("请输入顶点个数以及变数:\n"); scanf("%d%d",&G.vexnum,&G.arcnum); getchar(); printf("请输入各顶点:\n"); for(i=0;i<G.vexnum;i++){ scanf("%c",&G.vexs[i]); } for(i=0;i<G.vexnum;i++){ for(j=0;j<G.vexnum;j++){ G.arcs[i][j].adj=0; } } printf("请输入各个边:\n"); for(i=0;i<G.arcnum;i++){ getchar(); scanf("%c%c",&x,&y); loc1=LocateVex(G,x); loc2=LocateVex(G,y); G.arcs[loc1][loc2].adj=1; G.arcs[loc2][loc1].adj=1; } return 1; }
深搜:
从某个顶点V触发,访问次顶点,然后依次从V的未被访问的邻接点出发深度优先遍历图,直到图中所有和V有路径相同的顶点都被访问到。
如果是一个连通图,就结束。如果不是连通图,就会继续深搜。
如此时图中尚有顶点未被访问,则另选图中一个未被访问的顶点做起始点,重复上述过程,直到图中所有顶点都被访问到。
int *visit=(int *)malloc(sizeof(int)*MAX_VERTEX_NUM);//用于判断是否已访问过 int firstadj(MGraph G,int v){//返回与V邻接的顶点的下标 int loc=-1; int i; for(i=0;i<G.vexnum;i++){ if(G.arcs[v][i].adj == 1){ loc=i; break; } } return loc; } int nextadj(MGraph G,int v,int w){//返回与v邻接的在w之后的顶点下标 int loc=-1; int i; for(i=w+1;i<G.vexnum;i++){ if(G.arcs[v][i].adj == 1){ loc=i; break; } } return loc; } Status DFS(MGraph G,int v){//对顶点V深搜 int w; visit[v]=1; for(w=firstadj(G,v);w!=-1;w=nextadj(G,v,w)){ if(!visit[w]){ DFS(G,w); } } return 1; } int p=0;//用于统计图的连通分量数 Status DFSTraver(MGraph G,int &p)//深搜,同时确定图的连通分量数目 { int i; p=0; for(i=0;i<G.vexnum;i++){ visit[i]=0; } for(i=0;i<G.vexnum;i++){ if(!visit[i]) { DFS(G,i); p++; } } return 1; }
割边的判断以及输出函数
int One[MAX_VERTEX_NUM][MAX_VERTEX_NUM];//用于存储桥 int Twogb[MAX_VERTEX_NUM][MAX_VERTEX_NUM];//用于存储边 int Qiao(MGraph G)//用于确定哪些边是桥,并将桥标记到数组One中,用1表示 { int i,j,p1; for(i=0;i<G.vexnum;i++) for(j=i;j<G.vexnum;j++) { One[i][j]=0; Twogb[i][j]=0; if(G.arcs[i][j].adj==1){ G.arcs[i][j].adj=0;//删除边 G.arcs[j][i].adj=0;//删除边 DFSTraver(G,p1); if(p1>p) One[i][j]=MAX_VERTEX_NUM+1;//说明是桥 G.arcs[i][j].adj=1;//添加回来 G.arcs[j][i].adj=1; //添加回来 } } return 1; } int printfQ(MGraph &G) //输出桥 { int i,j; for(i=0;i<G.vexnum;i++) for(j=i;j<G.vexnum;j++) if(One[i][j] == MAX_VERTEX_NUM+1){ printf(" %c%c \n",G.vexs[i],G.vexs[j]); G.arcs[i][j].adj=0;//删除边 G.arcs[j][i].adj=0;//删除边 } printf("\n"); }
边割集的判断以及输出
int GeBianJi2(MGraph G,int k1,int k2,int num) ; int Flag(MGraph G,int Twogb[][20]); int n=0; int GeBianJi(MGraph G,int k1,int k2,int x)//用于判断边,并输出 ,并不输出桥 x:嵌套层次 { int i,j,p1=0,w,n=0,b=0,flag=0,i1,j1; k2=(k2 == 0 )? (i+1): k2; for(i=k1;i<G.vexnum;i++) { k2=(i == k1) ? k2 :(i+1); for(j=k2;j>=i&&j<G.vexnum;j++) { if(G.arcs[i][j].adj==1)//如果是普通边就继续 { G.arcs[i][j].adj=0;//删除边 G.arcs[j][i].adj=0;//删除边 DFSTraver(G,p1); if(p1 == p){//说明依然连通 Twogb[i][j]=1; GeBianJi(G,i,j+1,++x); }else{ Twogb[i][j]=1; if(Flag(G,Twogb) == 1){ for(i1=0;i1<G.vexnum;i1++) for(j1=i1+1;j1>=i1&&j1<G.vexnum;j1++) if(Twogb[i1][j1]==1 && b<= x) { printf(" %c%c ,",G.vexs[i1],G.vexs[j1]);b++; } printf("\n"); b=0; } } Twogb[i][j]=0; G.arcs[i][j].adj=1;//添加回来 G.arcs[j][i].adj=1; //添加回来 } } } return 1; } int numbers=0; int f=0; int GeBianJi2(MGraph G,int k1,int k2,int num) { int i,j,p1=0; k2=(k2 == 0 )? (i+1): (k2+1); for(i=k1;i<G.vexnum;i++) { k2=(i == k1) ? k2 :(i+1); for(j=k2;j>=i&&j<G.vexnum;j++) { if(Twogb[i][j]==1)//如果不是桥就继续 { numbers++; if(numbers < num){ G.arcs[i][j].adj=0;//删除边 G.arcs[j][i].adj=0;//删除边 DFSTraver(G,p1); if(p1 == p){//说明依然连通 GeBianJi2(G,i,j,num); }else if(p1 > p){ f++; } G.arcs[i][j].adj=1;//添加回来 G.arcs[j][i].adj=1; //添加回来 --numbers; }else{ --numbers; return 0; } } } } return f; } int Flag(MGraph G,int Twogb[][20]){ //用于二次判断边 int i,j,flag=1,num=0; f=1,numbers=0; for(i=0;i<G.vexnum;i++) for(j=i+1;j>=i&&j<G.vexnum;j++) if(Twogb[i][j] == 1) { G.arcs[i][j].adj=1; G.arcs[j][i].adj=1; num++;//用于避免自身 } if(num == 2) return 1; flag=GeBianJi2(G,0,0,num); return flag; }
最后就是主函数
int main() { int p1,i=0,j; MGraph G; CreateG(G); DFSTraver(G,p);//调用连通性判断 p1=p;//此时,p1就是图的连通分量个数 printf("图的连通分量个数%d\n",p1); Qiao(G); //然后,桥的获取,因为桥是一条边 printf("桥有:\n"); printfQ(G); DFSTraver(G,p); p1=p; printf("图的连通分量个数%d\n",p1); printf("割边集:\n"); GeBianJi(G,0,0,0); printfQ(G); return 1; }
这个实验的效果图:
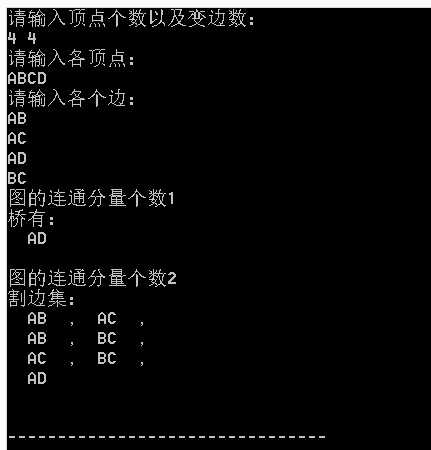
这是学习期间的第一个写的比较多的c语言作业。写的也比较粗糙,但是自己觉得真的挺尽力了,以后还是要多学习。
努力努力再努力。
标签:std 返回 主函数 visit 哪些 深度优先遍历 efi ring include
原文地址:http://www.cnblogs.com/senhaishusheng/p/7069633.html