标签:style blog http color strong ar for 文件 数据
排序六:直接选择排序
直接选择排序也是一种简单的排序方法,它的基本思想是:第一次从data[0]~data[n-1]中选取最小值,与data[0]交换,第二次从data[1]~data[n-1]中选取最小值,与data[1]交换,....,第i次从data[i-1]~data[n-1]中选取最小值,与data[i-1]交换,.....,第n-1次从data[n-2]~data[n-1]中选取最小值,与data[n-2]交换,总共通过n-1次,得到一个按排序码从小到大排列的有序序列。
int[] data= { 31, 23, 89, 10, 47, 68, 8, 22 };
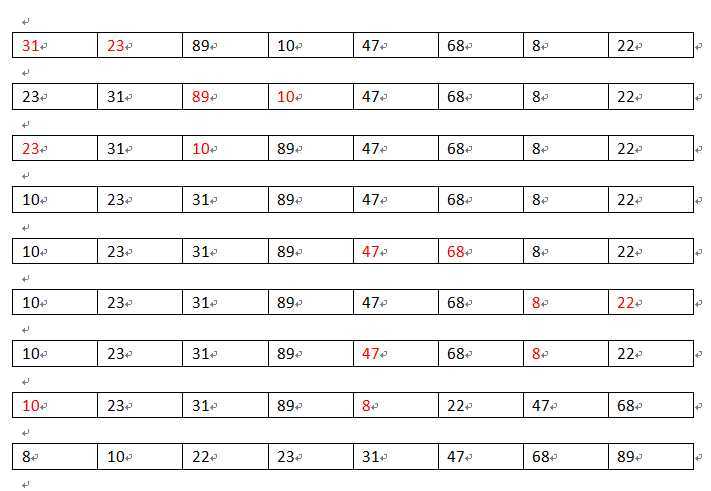
【31 23 89 10 47 68 8 22 】data[0]=31与最小data[6]=8交换
【8 23 89 10 47 68 31 22 】data[1]=23与后面最小值data[3]=10交换
【8 10 89 23 47 68 31 22 】data[2]=89与后面最小值data[7]=22交换
【8 10 22 23 47 68 31 89 】data[3]=23小于后面的值,不用交换
【8 10 22 23 47 68 31 89 】data[4]=47与后面最小值data[6]=31交换
【8 10 22 23 31 68 47 89 】data[5]=68与后面最小值data[6]=47交换
【8 10 22 23 31 47 68 89 】data[6]=68小于后面的值,不用交换
排序完成
从小到大排序:
public class Sort { public static void main(String[] args) { int[] data = { 31, 23, 89, 10, 47, 68, 8, 22 }; selectSort(data); showData(data); } // 打印数组 private static void showData(int[] data) { for (int i = 0; i < data.length; i++) { System.out.print(data[i] + " "); } } // 直接选择排序 private static void selectSort(int[] data) { int n = data.length; int i, j, k; int t; for (i = 0; i < n - 1; i++) {// 做第i趟排序(1≤i≤n-1) k = i; for (j = i + 1; j < n; j++) { // 在当前无序区data[i..n]中选key最小的记录data[k] if (data[j] < data[k]) { k = j; // k记下目前找到的最小关键字所在的位置 } } if (k != i) { // 交换data[i]和data[k] t = data[i]; data[i] = data[k]; data[k] = t; // t作暂存单元 } } } }
排序七:堆排序
堆实际上是一棵完全二叉树,其任何一非叶节点满足性质:Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]或者Key[i]>=Key[2i+1]&&key>=key[2i+2]。
堆分为大顶堆和小顶堆,满足Key[i]>=Key[2i+1]&&key>=key[2i+2]称为大顶堆,满足 Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]称为小顶堆。由上述性质可知大顶堆的堆顶的关键字肯定是所有关键字中最大的,小顶堆的堆顶的关键字是所有关键字中最小的。
2.用大根堆排序的基本思想:
(1)用大根堆排序的基本思想
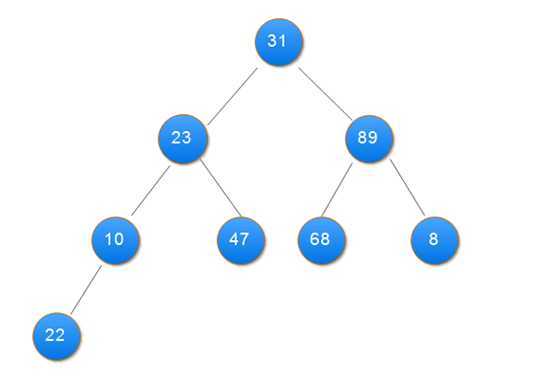
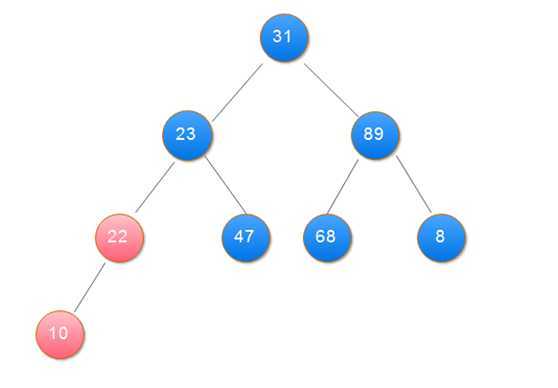
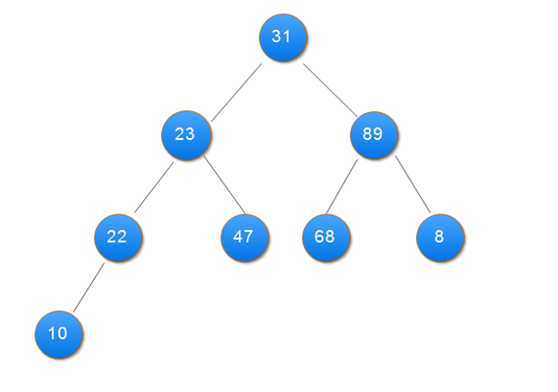
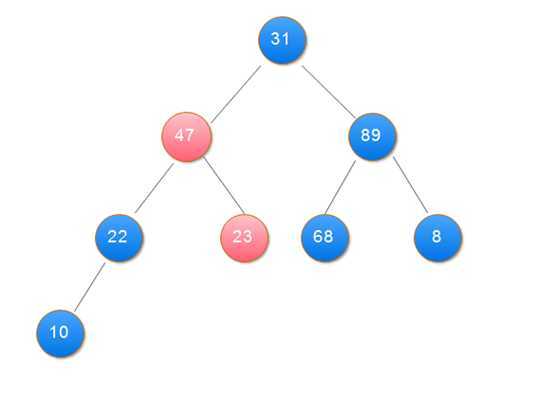
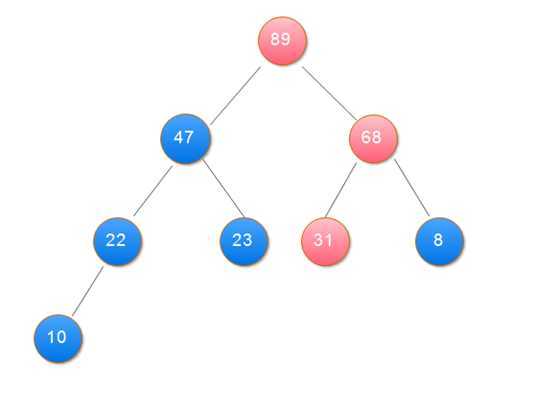
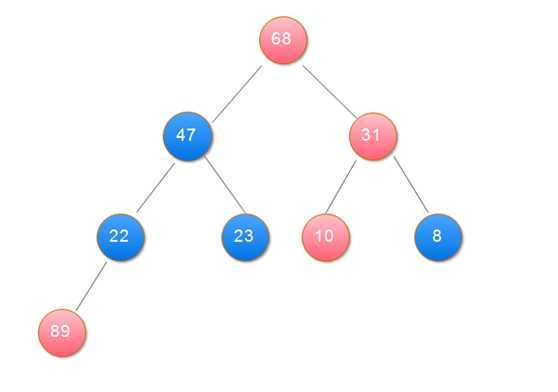
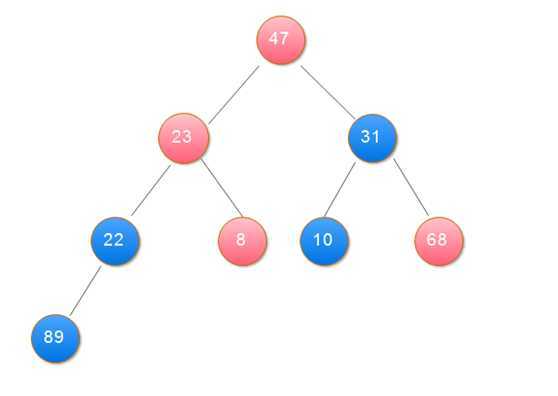
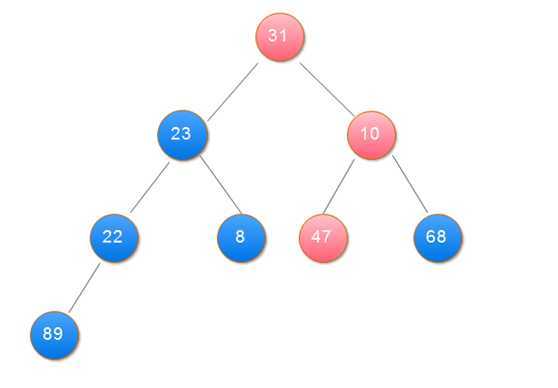
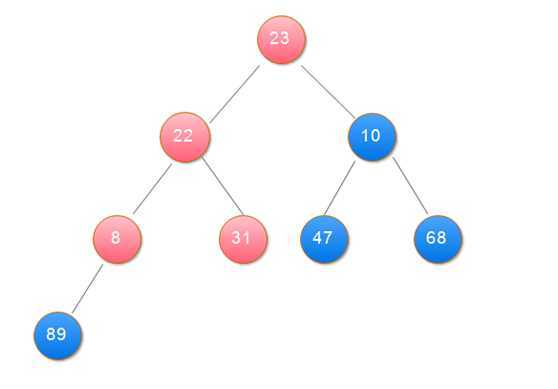
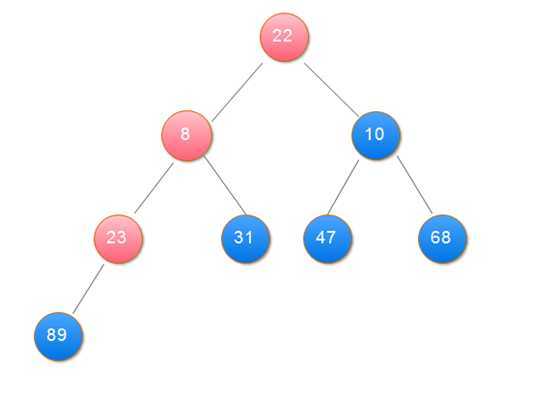
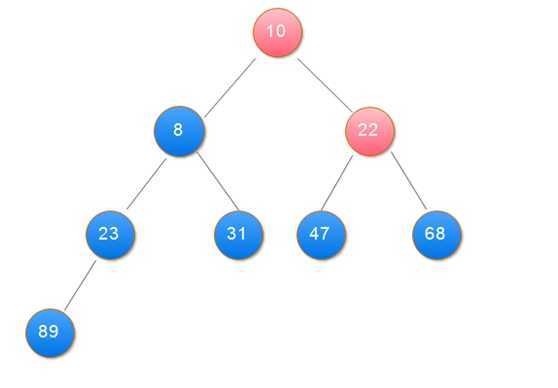
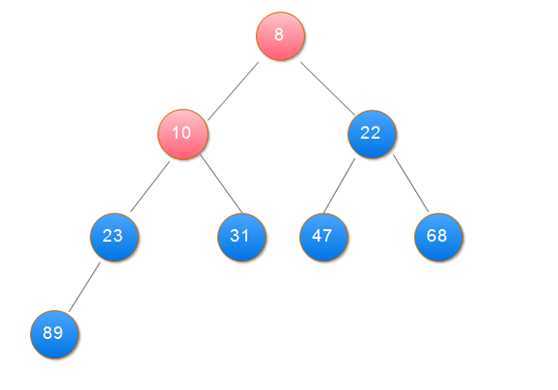
public class Sort { public static void main(String[] args) { int[] data = { 31, 23, 89, 10, 47, 68, 8, 22 }; heapSort(data); showData(data); } // 打印数组 private static void showData(int[] data) { for (int i = 0; i < data.length; i++) { System.out.print(data[i] + " "); } } // 堆排序 筛选算法 private static void sift(int[] data, int i, int n) { int j, temp; temp = data[i]; j = 2 * i + 1; while (j < n) { if (j + 1 < n && data[j + 1] > data[j]) // 在左右孩子中找最大的 j++; if (data[j] <= temp) break; data[i] = data[j]; // 把较大的子结点往上移动,替换它的父结点 i = j; j = 2 * i + 1; } data[i] = temp;// 堆顶记录填入适当位置 } // 创建大项堆算法 private static void buildHeap(int[] data, int n) { int i; for (i = n / 2 - 1; i >= 0; i--) {// 建立初始堆 sift(data, i, n); } } // 堆排序 private static void heapSort(int[] data) { int n = data.length; int i; int t; buildHeap(data, n); for (i = n - 1; i >= 1; i--) { t = data[i];// 将堆顶记录与最后一个记录交换 data[i] = data[0]; data[0] = t; sift(data, 0, i);// 调整堆 } } }
排序八:归并排序
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。
归并操作的基本思想:
1.申请一个临时数组,使其大小为要排序的数组一样大,排序时用来临时存放数据。
2.将要排序的数据以中点分成两组数据各自排序,各自排序也是以各自的中点分成两组数据直到递归分割数据到基本单位;
3.从两个已经排序序列的起始位置比较,选择相对小的元素放入临时数组里,并比较下一位置的数据,直到超出序列尾。
4.将另一序列剩下的所有元素直接复制到临时数组,最后临时数组数据全部赋值给要排序的数组,这样就排序完成了。

public class Sort { public static void main(String[] args) { int[] data = { 31, 23, 89, 10, 47, 68, 8, 22 }; mergeSort(data); showData(data); } // 打印数组 private static void showData(int[] data) { for (int i = 0; i < data.length; i++) { System.out.print(data[i] + " "); } } // 归并排序 public static void mergeSort(int[] list) { int length = list.length; int[] temp = new int[length];// 临时数组 recMergeSort(list, temp, 0, length - 1); } // 递归分割数据到基本单位 private static void recMergeSort(int[] list, int[] temp, int low, int upper) { if (low == upper) { return; } else { int mid = (low + upper) / 2; recMergeSort(list, temp, low, mid); recMergeSort(list, temp, mid + 1, upper); merge(list, temp, low, mid + 1, upper); } } // 归并操作将基本单位归并成整个有序的数组 private static void merge(int[] list, int[] temp, int left, int right, int last) { int j = 0; int lowIndex = left; int mid = right - 1; int n = last - lowIndex + 1; while (left <= mid && right <= last) { if (list[left] < list[right]) { temp[j++] = list[left++]; } else { temp[j++] = list[right++]; } } while (left <= mid) { temp[j++] = list[left++]; } while (right <= last) { temp[j++] = list[right++]; } for (j = 0; j < n; j++) { list[lowIndex + j] = temp[j]; } } }
标签:style blog http color strong ar for 文件 数据
原文地址:http://www.cnblogs.com/ycclmy/p/3946463.html