标签:matlab
matlab与线性代数实验基础
作者:xuan97916
一、行列式
1、行列式的输入
方括号内逐行键入元素,同一行元素用逗号或者空格,两行元素之间用分号隔开。
在命令的末尾使用分号会终止输出!
A=[1,2,3;4,5,6;7,8,9]
2、行列式元素的表示
可以用一个下标表示(从上到下之字形)也可以用两个下标表示(行列)如
A(1,2) =A(4)
3、行列式的基本运算
· (1)读取整行:A(行数,:)
(2)读取整列:A(:,列数)
(3)读取行列式中的部分行列b=A([行数,行数```],[列数,列数```])
(4)去掉行列式中的某些行列
A([行数,行数,…],:) =[ ]
A(:,[列数,列数,…]) =[ ]
(5)计算行列式的值
det(A)
二、矩阵
1、矩阵的输入
生成m阶单位方阵:eye(m)
生成m*n阶单位矩阵:eye(m,n)
生成m阶全1方阵:ones(m)
生成m*n阶全1矩阵:ones(m,n)
生成m阶全0方阵:zero(m)
生成m*n阶全0矩阵:zeros(m,n)
2、矩阵的输入
加法:A+B
减法:A-B
数乘:k*A
矩阵乘法:A*B
矩阵转置:A’或者Transpose[A]
矩阵的逆:inv(A)
矩阵的行列式 det(A)
矩阵的幂:A^m
3、矩阵的相关函数
(1)生成矩阵的行数与列数:size(A)
第一个数是矩阵的行数,第二个数是矩阵的列数。
(2)生成对角矩阵:diag(A)
生成对角矩阵主对角线上的元素
(3)生成上三角矩阵:triu(A)
(4)生成下三角矩阵:tril(A)
三、矩阵的应用
1、向量组的秩:rank(A)
2、判断线性相关性
一般步骤(1)输入向量组
(2)用A’将行向量转置为列向量
·· (3)用rref(A)命令求秩
例:判断向量组a1=(1 2 0 1), a2=(1 3 0 -1), a3=(-1 -1 1 0)是否线性相关,并求秩。
>> A=[1 2 0 1;1 3 0-1;-1 -1 1 0]; %输入矩阵
>>A=A’ % 将行向量转置为列向量再求秩
>>rank(A) %求秩
Ans = 3
(注意:当rank(A)等于向量组个数时,线性无关,否则线性相关)
3、求向量组的极大无关组
一般步骤:(1)输入向量组,并将其进行转置
(2)化为分数形式
(3)将向量化为行最简型
(4)对线性相关性进行判断
注:将矩阵化为行最简型的命令为:rref(A)或者rrefmovie(A)
例1:求下列向量组的秩和一个极大线性无关组,并将其余向量用该极大无关组线性表示。
a1=(2 -1 3 5),a2=(4 -3 1 3),a3=(3 -2 3 4),
a4=(4 -1 15 17),a5=(7 -6 -7 0)
>> A=[2 -1 3 5;4 -3 1 3;3 -2 3 4;4 -1 15 17;7 -6 -7 0];
>> A=A′ %将行向量转化为列向量进行运算
>> format rat %分数格式形式
>> rref(A) %将A变换为行最简型
ans =
1 0 0 2 1
0 1 0 -3 5
0 0 1 4 -5
0 0 0 0 0
因为前三行的向量均不全为0,且第1,2,3列的均为1开头,所以a1,a2,a3为一个极大无关组。
例2:求下列向量组的秩和一个极大线性无关组,并将其余向量用该极大无关组线性表示。
a1=(1,-2,2,3),a2=(-2,4,-1,3),a3=(-1,2,0,3),a4=(0,6,2,3),a5=(2,-6,3,4)
解:
A=[1,-2,2,3;-2,4,-1,3;-1,2,0,3;0,6,2,3;2,-6,3,4]
>> A=A′ %将行向量转化为列向量进行运算
>> format rat %分数格式形式
>> rref(A) %将A变换为行最简型
A1,a2,a4为一个线性无关组,a3,a5可用其其线性表示
3、线性方程组的求解
(1)使用克莱姆法则求解
>> A=[2 1-5 1;1 -3 0 -6;0 2 -1 2;1 4 -7 6]; %输入系数矩阵
>>D=det(A) %判断解的情况
D = 27
>> C1=A;C2=A;C3=A;C4=A;b=[8;9;-5;0];
%将A赋值给不同变量
>> C1(:,1)=b;D1=det(C1); %将某行替换为系数列
x1=D1/D %x求解x1
x1 = 3
>> C2(:,2)=b;D2=det(C2);x2=D2/D
>> C3(:,3)=b;D3=det(C3);x3=D3/D
>> C4(:,4)=b;D4=det(C4);x4=D4/D
(2)使用矩阵左除法求线性方程的解
线性方程组AX=B的一个解为X=A\B。
例:利用左除法求解上题中线性方程组的解.
>> A=[2 1 -5 1;1 -3 0 -6;0 2 -1 2;1 4 -7 6];
>>rank(A)
>> b=[8;9;-5;0];
>> x=A\b %左除法
x =
3.0000
-4.0000
-1.0000
1.0000
(3)利用矩阵的行(列)初等变换求线性方程组的通解
基本步骤:(1)将线性方程组表示成增广矩阵的形式;
(2)对增广矩阵实行初等变换,使增广矩阵转化为行阶梯形矩阵;
(3)得到方程组的解。
例:求解线性方程组
>>A=[1,1,1,1;0,1,-1,1;2,3,1,3]; %方程组的增广矩阵
>>F=rref(A); %将方程组增广矩阵化为行阶梯形矩阵
>>F %输出增广矩阵的行阶梯形矩阵
F =
1 0 2 0
0 1 -1 1
0 0 0 0
由该阶梯形矩阵,可得方程组:x1=-2x3 x2=x3+1
方程组解为:
(4)求非齐次线性方程组的通解
非齐次线性方程组需要先判断是否有解,若有解,再进一步求通解。
一般步骤为:
第一步:判断AX=b是否有解,若有解则进行第二步;(R(A)与R(A,b)比较,即比较系数矩阵的秩和增广矩阵的秩)
第二步:求AX=b的一个特解;(矩阵除法)
第三步:求AX=0的通解;(利用null命令)
第四步:AX=b的通解:AX=0的通解+AX=b的一个特解。
例:判断方程组
%第一步:判断系数矩阵与增广矩阵的秩
>> A=[1 -1 1 -1;-1 1 1 -1;2 -2 -1 1]; %系数矩阵A
>> b=[1;1;-1]; %常数b
>> rank(A) %系数矩阵的秩
ans =
2
>> rank([A,b]) %增广矩阵的秩
ans =
2
%求通解
化行最简形,用rref命令
>> rref([A,b])
ans =
1 -1 0 0 0
0 0 1 -1 1
0 0 0 0 0
取x2,x4为自由变量,从而通解为:x1=x2,x3=x4+1
(2)先求出特解及导出组的基础解系, 用命令null,例如:
>>x0=A\b %方程组的一个特解
x0 =
0
0
1
0
>>x1=null(A) %求导出组的基础解系
x1 =
-0.7071 0
-0.7071 0
-0.0000 0.7071
-0.0000 0.7071
故原方程组的通解为
(x1,x2,x3,x4)=(0,0,1,0)+c1(-0.7071,-0.7071,0,0) +c2(0,0, 0.7071, 0.7071),c1,c2为任意常数.
null是用来求齐次线性方程组的基础解系的,加上‘r‘则求出的是一组最小正整数解,如果不加,则求出的是解空间的规范正交基。(x1=null(A,‘r‘))
四、运用矩阵运算进行图像处理
1、图像的读写
Imread:读入各种图像文件
[I,map]=imread(‘face.gif’)
Imwrite:输出图像,将图像数据矩阵写入文件中
Imwrite(i,‘face.gif’)
Imwrite(i,map,‘face.gif’)
2、图像的显示
Imshow:显示各种图像的函数
其中I是图像数据矩阵,map是对应的颜色矩阵:
[I,map]=imread(‘face.gif’)
Imshow(I,map)
3、窗口的多开
[I,map]=imread(‘face.gif’)
Imshow(i.map)
[j,map]=imread(‘flowers.gif’)
Figure,imshow(j,map) %实现(j,map)窗口的多开
4、查看图像的大小
[I,map]=imread(‘face1.gif’)
Size(i)
Ans=140 144 %表示高为140 宽为144
5、多幅图像显示在同一个对话框中
Subplot(n,m,p)将一个显示对话框分成m行n列,并显示第p幅图像
Subplot(2,2,3),imshow(I3),title(‘I3图像’)
表示将一个图像显示对话框分成2行2列,并在第3个位置显示I3图像,图像标题为“ I3图像”
6、读取图像的基本操作
例1:读取gif类型的图像
>>[i.map]=imread(‘face.gif’)
>>Size(i)
>>size(map)
>>imshow(i.map)
>>A=[0 0 0;0 1 0;0 0 1] %设置颜色变换矩阵A
>>map=map*A %利用矩阵修改颜色表数据map
Imshow(I,map)
例2:读取jpg类型的图像文件
>>[I,map]=imread(‘face.jpg’)
>>size(i)
>>size(map)
>>imshow(I,map)
>>i((:,:,2)=i(:,:,2)*0 //将绿色矩阵的值设置为0
>>imshow(I,map)
7、图像相加、相减、数乘
(1)相加:降低图像噪声的影响
(2)相减:将两图的差异显示出来
(3)数乘:数乘大于1的数,亮度增加;
数乘小于1的数,图像变暗
五、在处理图像水印中的应用
将水印嵌入到图像中实质上是进行两个图像矩阵的加法运算
去掉水印则是进行矩阵减法运算。
(1)例:利用矩阵运算往图像中嵌入文字水印的例子。
1.读取原图像hudie.jpg到I中。
>>I=imread(‘hudie.jpg‘);
>>imshow(I)
2.读取原图像hudie.jpg的大小,并将图像的高、宽存到m、n中。
>>s=size(I);
>> m=s(1)
>> n=s(2)
3.读取水印图像huaduo_sy.jpg到J中,并将图像大小调整成与原图像相同。使用imresize()函数可以改变图像的大小。
>>J=imread(‘xiaohui_sy.jpg‘);
>>imshow(J);
>>J1=imresize(J,[m,n]); //将图像矩阵J的高、宽变为m*n
4.将水印图像的红、绿、蓝三个颜色矩阵乘上系数0.3,以降低像素点颜色的饱和度。
>>J1(:,:,1)= J1(:,:,1)*0.3;
>>J1(:,:,2)= J1(:,:,2)*0.3;
>>J1(:,:,3)= J1(:,:,3)*0.3;
5.将原图像与改变后的水印图像相加,嵌入水印。
>>I1=im2double(I);
>>J2=im2double(J1);
>> A=I1+J2;
>>imshow(A);
6.将嵌入水印后的图像保存在hudie_add.jpg文件中。
>>imwrite(A,‘hudie_add.jpg‘)
7.将处理过的数字图像水印保存在xiaohui_syh.jpg文件中。
>>imwrite(J1, ‘xiaohui_syh.jpg‘)
(2)去掉数字图像水印
例:利用矩阵运算去掉图像中的数字图像水印的例子。
1.读取嵌入水印的图像hudie_add.jpg到SA中。
>>SA=imread(‘hudie_add.jpg‘);
>> imshow(SA)
2.读取处理过的水印图像xiaohui_syh.jpg到I中。
>> I=imread(‘xiaohui_syh.jpg‘);
3.将嵌入水印后的图像与处理后的水印图像相减,去掉水印。
>> SA1=im2double(SA);
>> I1=im2double(I);
>> A=SA1-I1;
>> imshow(A);
六、利用矩阵运算实现图形的几何变换
1.二维图形变换
2、二维图形组合变换
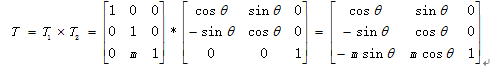
3、plot函数
(1)plot(Y)
如果Y 是向量,则以向量的索引为横坐标,以向量元素值为纵坐标绘制图形,以直线段顺序连接各点;如果 Y 是矩阵,则绘制 Y 的各列;如果 Y是复向量,则以复数的实部为横坐标,虚部为纵坐标绘制图形
(2)plot(x,y)
命令中的 x 和y 可以为向量和矩阵,当x和y的结构不同时,有不同的绘制方式。
–x、y 均为 n 维向量时,以x 的元素为横坐标,y 的元素为纵坐标绘制图形。
–x 为 n 维向量,y 为m×n 或 n×m 矩阵时,以 x 的元素为横坐标,绘制 y 的 m 个n 维向量。
–x、y 均为 m×n 矩阵时,以x 的各列为横坐标,y 的对应列为纵坐标绘制图形。
(3)plot(x,y,LineSpec)
该命令中加入了 LineSpec参数,用于对图形外观的控制,包括线条的形状、颜色和点的形状、颜色。该参数的常用设置选项如表所示。
(4)图形的比例变换
其中a代表横坐标放大的系数,d代表纵坐标放大的系数
例1:由(1,2)、(4,5)、(3,6)三点组成的三角形,将其横坐标和纵坐标同时放大2倍,求所得三角形的三点坐标。
>>x=[1;4;3;1]; %将第一个坐标在末尾重复写一遍表示图形闭合
>>y=[2;5;6;2];
>>A=[x y];
>>C=[2 0;0 2]; %C为变换矩阵,使得其横纵坐标同时变为2倍
>>B=A*C;
>>a=B(:,1);
>>b=B(:,2);
>> plot(x,y,‘:‘,a,b) %显示两个图形的对比状态
(5)图形的对称变换
A)对称x轴
变换矩阵为:
B)对称Y轴
C)对称坐标原点
(6)图形的旋转变换
图形在平面上绕坐标原点逆时针旋转 角,图形发生旋转变换。
变换为:
例:由(1,2)、(4,5)、(3,6)三点组成三角形,求将其逆时针旋转45弧度角后所得的图形。
x=[1;4;3;1];
y=[2;5;6;2];
A=[xy];
C=[cos(45)sin(45);-sin(45) cos(45)];
B=A*C;
a=B(:,1);
b=B(:,2);
plot(x,y,‘:‘,a,b)
(7)平移变换
将图形沿X方向移动距离m,沿Y方向移动距离n,图形形状保持不变,图形各点的坐标分别增加了平移量m和n。
平移变换的矩阵运算表示为 :
例:由(1,2)、(4,5)、(3,6)三点组成三角形,求将其横坐标向右平移4,纵坐标向上平移5后所得的图形。
x=[1;4;3;1];
y=[2;5;6;2];
z=[1;1;1;1];
A=[x y z];
C=[1 00;0 1 0;4 5 1];
B=A*C;
a=B(:,1);
b=B(:,2);
plot(x,y, ‘:‘,a,b)
(8)综合应用
例:由(0,0)、(2,0)、(1,2)三点组成三角形,将其各点坐标沿轴向上平移4后,再绕坐标原点逆时针旋转45弧度后,求所得的图形。
x=[0;2;1;0];
y=[0;0;2;0];
z=[1;1;1;1];
A=[x yz];
C=[1 0 0;0 1 0;0 4 1];
D=[cos(45)sin(45) 0;-sin(45) cos(45) 0;0 0 1]; %如果进行了平移变化后,再进行旋转变换时,注意将旋转变化的矩阵的阶数提高,第一第二列补0,第三列为0 0 1
E=C*D;
B=A*E;
a=B(:,1);
b=B(:,2);
plot(x,y, ‘:‘,a,b)
七、Hill加密算法
1、基本步骤
加密:
(1)将明文信息分组,每组s个数值,组成n组明文向量
(2)选定一个加密密钥,其阶数为s,将这个密钥分别左乘每个数值矩阵
(3)对矩阵进行模26运算,得到密文向量
例:
解密:
即将密文按同样方式分组,用逆矩阵对其进行处理,对出现的负值加上26得到明文向量
>>x1=[19;20;21]; %密文1
>>x2=[4;25;13]; %密文2
>>x3=[1;20;8]; %密文3
>>A=[1 2 3;1 1 2;0 1 2] %加密密钥
>>det(A) %求矩阵的行列式,判断是否可逆
ans = -1
>>B=inv(A) %B是A的逆
>>X1=A*x1;
>>X2=A*x2;
>>X3=A*x3;
>>y1=mod(X1,26)
>>y2=mod(X2,26)
>>y3=mod(X3,26)
>>x1=B*y1
>>x2=B*y2
>>x3=B*y3
最后,生成明文信息。MATLAB代码如下:
>> x1=mod(x1,26)
>>x2=mod(x2,26)
>>x3=mod(x3,26)
注意:要根据密码表的总数来确定模除法的数值
作者:xuan97916
参考资料: [1]王艳君,赵明华,李文斌,线性代数实验教程[M],清华大学出版社,2011.12
本文出自 “xuan97916” 博客,转载请与作者联系!
标签:matlab
原文地址:http://xuan97916.blog.51cto.com/12114604/1941578