标签:grid 自己 环境 strong height 循环 空闲 机器 运动
- HectorSLAM的整体逻辑
- 激光匹配
- 地图构造
- 地图更新
- 500行代码重写一个LidarSLAM
- 测试数据的准备,和测试数据读取模块的编写
- GUI编写
- 地图模块的编写
- 核心模块的编写
- 主循环
- 匹配算法
首先绘制一张以扫描匹配为核心的SLAM(例如Hector,Karto_slam,Cartographer..)大概的流程图:
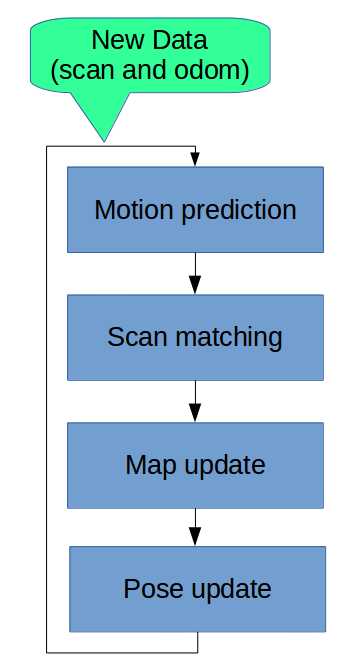
基本上以这一类SLAM流程分以下几个部分:
因为原版的Hector并没有使用车轮odometry。所以运动预测部分,仅为根据前一个状态的位置和速度的预测。所以我们直接从跳过motion prediction,下面从2.scan matching(扫描匹配)开始谈起。
所谓匹配就是把从传感器得到的数据和已经知道的地图进行匹配。我们首先假定周围环境是静态的,在静态的环境中,传感器数据应该和已知的地图情报应该高度一致才对。所以在没有噪音的情况下以下方程应该成立:
$\sum _{i=0}^{n}\left[ 1-M\left( S_{i}\left( \xi \right) \right) \right] = 0$
其中$\xi=\left(p_x,p_y,\psi\right)$代表机器人的姿态(x坐标,y坐标,角度)
Si代表,i号激光束,在姿态下ξ的照射到的障碍物坐标。
M代表某坐标为障碍物的概率。1为100%为障碍物,0为100%空闲区域
在传感器没有噪音,地图情已知且没有误差的的情况下,可以求解以上方程,得到未知量ξ(姿态)。直观上来说就是调整姿态使得所有的激光都正确的测量到障碍物。但现实的情况却没有怎么完美,传感器有噪音,地图有误差,且部分未知。所以我们转而求解以下最小二乘法:
$argmin_{\xi}\sum _{i=0}^{n}\left[ 1-M\left( S_{i}\left( \xi \right) \right) \right]^2$
这个公式的就求解方法,在论文的公式(9)~(13)有推导过程。这里虽然不推导(论文已经足够详细),但是仍然建议自己推导一次加深理解。
根据下面的方程我们似乎已经可以通过扫描匹配解出机器人姿态了。
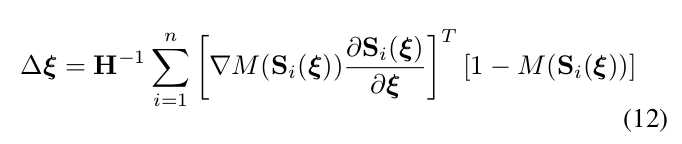
![]()
我们似乎可以解出机器人姿态了。。。其实我们还不行的。。。因为求解以上(12)(13)是需要求M的偏导的,我们知道求解偏导的是需要连续空间的,但Hector使用的格子地图(grid map)存在于离散的空间中。
所以,首先我们需要一些方法把我们的离散的格子地图,转换为可以求导的连续地图。
标签:grid 自己 环境 strong height 循环 空闲 机器 运动
原文地址:http://www.cnblogs.com/scomup/p/7075296.html