标签:with cstring sid for lang opera tar cst common
题目链接:
http://poj.org/problem?id=1673
题目描述:
Description
Input
Output
Sample Input
2 0.0 0.0 9.0 12.0 14.0 0.0 3.0 4.0 13.0 19.0 2.0 -10.0
Sample Output
9.0000 3.7500 -48.0400 23.3600
题目大意:
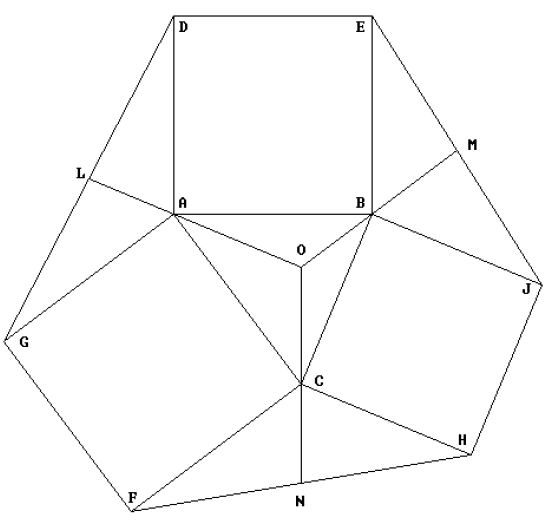
如图,将三边延拓成正方形,然后连线取中点,连线求交点
思路:
证明点O为三角形垂心
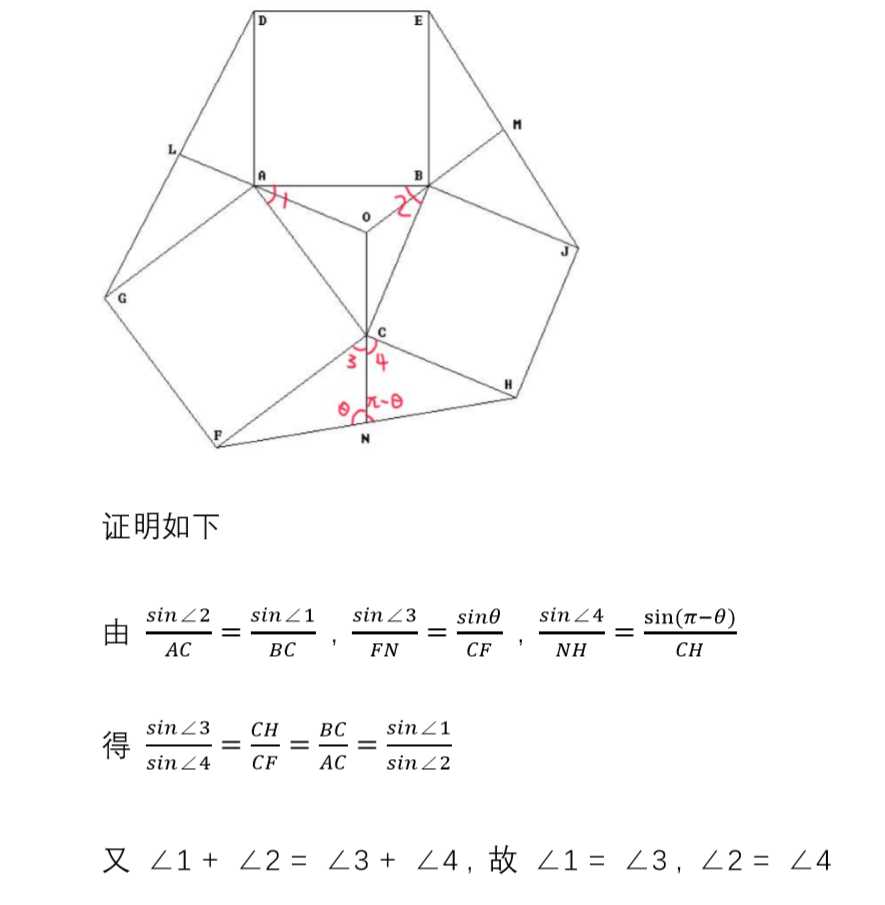
然后可知 CO ⊥ AB
另两条边同理
求垂心即可
PS:输出需要加一个EPS,避免-0.000
代码:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <cmath> 6 using namespace std; 7 8 const double EPS = 1e-8; //精度系数 9 const double PI = acos(-1.0); //π 10 11 struct Point { 12 double x, y; 13 Point(double x = 0, double y = 0) :x(x), y(y) {} 14 const bool operator < (Point A)const { 15 return x == A.x ? y < A.y : x < A.x; 16 } 17 }; //点的定义 18 19 typedef Point Vector; //向量的定义 20 21 Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); } //向量加法 22 Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); } //向量减法 23 Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); } //向量数乘 24 25 Vector Rotate(Vector A, double rad) { 26 return Vector(A.x*cos(rad) - A.y*sin(rad), A.x*sin(rad) + A.y*cos(rad)); 27 } //逆时针旋转rad度 28 29 Point LineIntersectionPoint(Point A1, Point B1, Point A2, Point B2) { 30 double t1 = ((A1.y - A2.y)*(B2.x - A2.x) - (A1.x - A2.x)*(B2.y - A2.y)) / 31 ((B1.x - A1.x)*(B2.y - A2.y) - (B1.y - A1.y)*(B2.x - A2.x)); 32 return A1 + (B1 - A1)*t1; 33 } //返回直线交点 34 35 int main() { 36 Point A, B, C; 37 int n; 38 cin >> n; 39 while (n--) { 40 scanf("%lf%lf%lf%lf%lf%lf", &A.x, &A.y, &B.x, &B.y, &C.x, &C.y); 41 Vector v = Rotate(B - A, PI / 2), u = Rotate(C - B, PI / 2); 42 Point ans = LineIntersectionPoint(C, C + v, A, A + u); 43 printf("%.4lf %.4lf\n", ans.x + EPS, ans.y + EPS); 44 } 45 }
POJ1673 EXOCENTER OF A TRIANGLE(三角形垂心)
标签:with cstring sid for lang opera tar cst common
原文地址:http://www.cnblogs.com/hyp1231/p/7094273.html