标签:bsp pac dash for 个数 can 最小 事实表 stream
此文为博主原创题解,转载时请通知博主,并把原文链接放在正文醒目位置。
【题目描述】
a[1]=a[2]=a[3]=1
a[x]=a[x-3]+a[x-1] (x>3)
求a数列的第n项对1000000007(10^9+7)取余的值。
【输入格式】
第一行一个整数T,表示询问个数。
以下T行,每行一个正整数n。
【输出格式】
每行输出一个非负整数表示答案。
【样例输入】
3
6
8
10
【样例输出】
4
9
19
【数据范围】
对于30%的数据 n<=100;
对于60%的数据 n<=2*10^7;
对于100%的数据 T<=100,n<=2*10^9;
分析:
数据范围到了二十亿,显然不优化是绝对要TLE的(事实表明暴力只有60分)
由于这是一个加和递推式的形式,所以采用(矩阵)快速幂。
大佬说只要是形似这样的加和的题都可以用矩阵来解。
下面是AC代码,注释已经写得很详细了不再多说。矩阵这东西还是应该找人来讲,文字叙述起来太困难。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 6 using namespace std; 7 const int INF = 0x3f3f3f3f; 8 const int MOD = 1000000007; 9 10 long long s1[10][10],s2[10]; 11 long long tmp[10][10],base[10][10],ans[10][10]; 12 13 long long pow(int b) 14 { 15 for(int i = 1;i <= 4;i ++) 16 { 17 ans[i][i] = 1; 18 for(int j = 1;j <= 4;j ++) 19 base[i][j] = s1[i][j] % MOD; 20 } 21 //初始化ans为单位矩阵,base为构造矩阵 22 //以后每次数列+n时只需*base^n 23 while(b) 24 { 25 //b的值不为零,也就是二进制表示中还有1 26 if(b & 1) 27 { 28 for(int i = 1;i <= 4;i ++) 29 for(int j = 1;j <= 4;++ j) 30 tmp[i][j] = ans[i][j] % MOD; 31 //b&1判断当前位是否为1,是的话就用tmp存储ans 32 memset(ans,0,sizeof(ans)); 33 34 for(int k = 1;k <= 4;k ++) 35 for(int i = 1;i <= 4;i ++) 36 for(int j = 1;j <= 4;j ++) 37 ans[i][j] += ((tmp[i][k] % MOD) * (base[k][j] % MOD)); 38 //用tmp与base做矩阵乘法,求出ans 39 } 40 41 for(int i = 1;i <= 4;i ++) 42 for(int j = 1;j <= 4;j ++) 43 tmp[i][j] = base[i][j] % MOD; 44 //用tmp存储base 45 46 memset(base,0,sizeof(base)); 47 48 49 for(int k = 1;k <= 4;k ++) 50 for(int i = 1;i <= 4;i++) 51 for(int j = 1;j <= 4;j ++) 52 base[i][j] += ((tmp[i][k] % MOD) * (tmp[k][j] % MOD)); 53 //计算出新的base = base * base,实际上是倍增求base 54 b >>= 1; 55 } 56 return ((((ans[1][1]%MOD) * (s2[1]%MOD) % MOD) + ((ans[1][2]%MOD) * (s2[2]%MOD) % MOD))%MOD + (((ans[1][3]%MOD) *(s2[3]%MOD)) % MOD + ((ans[1][4]%MOD) * (s2[4]%MOD)) % MOD)%MOD) % MOD; 57 //返回的是ans与s2的乘积,此时ans为base的n次方,n与题目中的n相统一 58 } 59 int main() 60 { 61 int t,n; 62 scanf("%d",&t); 63 while(t) 64 { 65 scanf("%d",&n); 66 if((n == 1) || (n == 2) || (n == 3)) 67 { 68 printf("1\n"); 69 -- t; 70 continue; 71 } 72 else if(n == 4) 73 { 74 printf("2\n"); 75 -- t; 76 continue; 77 } 78 else if(n == 5) 79 { 80 printf("3\n"); 81 -- t; 82 continue; 83 } 84 memset(base, 0, sizeof(base)); 85 memset(tmp, 0, sizeof(tmp)); 86 memset(ans, 0, sizeof(ans)); 87 88 s2[1] = 3 ;s2[2] = 1;s2[3] = 1;s2[4] = 1; 89 //手算推出计算an需要an-2、an-3、an-4 90 //由上面四个量可以推出an+1、an-1、an-2、an-3 91 s1[1][1] = 1;s1[1][2] = 1;s1[1][3] = 0;s1[1][4] = 0; 92 s1[2][1] = 0;s1[2][2] = 1;s1[2][3] = 0;s1[2][4] = 1; 93 s1[3][1] = 0;s1[3][2] = 1;s1[3][3] = 0;s1[3][4] = 0; 94 s1[4][1] = 0;s1[4][2] = 0;s1[4][3] = 1;s1[4][4] = 0; 95 long long a = pow(n - 5) % MOD; 96 printf("%lld\n",a); 97 -- t; 98 } 99 return 0; 100 }
对于上面88—94行的来历再说一下。
思维过程:
假定我们已知an,需要求an+1,这时我们还需要知道an-2;
用an-2可以求得an-1,这时我们还需要知道an-4;
用an-4可以求得an-3,an-3又可以求得an-2。
将上述整理成矩阵的形式,大概就是这样的:
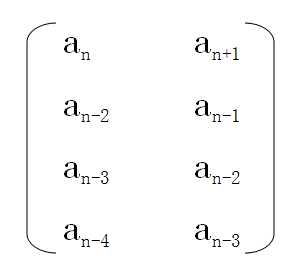
左边是条件,检验可知用左边的四个值可以求得右边的四个值。
而s1矩阵反映的就是从左边的值到右边的值的对应关系,用矩阵乘法计算。
关于矩阵乘法这里不再赘述,前面有一篇博客说过运算法则(尽管说得非常含糊),因为矩阵的东西确实很难用文字表达。。。
至于第95行,为什么pow(n-5),是因为左边的a下标最小是n-4,n-5(其实是n+1-5)与之对应。
标签:bsp pac dash for 个数 can 最小 事实表 stream
原文地址:http://www.cnblogs.com/shingen/p/7096192.html