标签:style http color 使用 strong 数据
本课程是由Prof.Daphne Koller主讲,同时得到了Prof. Kevin Murphy的支持,在coursera上公开传播。在本课程中,你将学习到PGM(Probabilistic Graphical Models)表示的基本理论,以及如何利用人类自身的知识和机器学习技术来构建PGM;还将学习到使用PGM算法来对有限、带噪声的证据提取结论,在不确定条件下做出正确的抉择。该课程不仅包含PGM框架的理论基础,还有将这些技术应用于新问题的实际技巧。
本课程包含以下主题:
1.贝叶斯网络(Bayesian network)和马尔科夫网络(Markov network)的表示,包括随时间变换的域和可变数量的实体的域的推理;
2.推理和推断的方法,包括精确推断(变量消除(variable elimination),势团树(clique tree)),近似推断(信仰传播的消息传递,马尔科夫链(蒙特卡洛方法));
3.PGM中,参数和结构化的学习方法;
4.在不确定条件下使用PGM进行决策;
不确定性是现实世界应用中不可避免的问题:我们几乎从未肯定地预测将要发生的时间,即使我们对于过去和现在的信息都了如指掌。概率理论为我们提供了用以对我因时而异、因地而异的belief建模的基础。这些belief可以结合个人的喜好来指导行动,甚至在选择观测中也能用到。
概率论自17世纪以来就存在,但直到最近我们才具有有效使用概率论的知识解决涉及许多相互联系的变量的大问题,这主要归功于PGM模型框架的发展。该框架,主要包含例如贝叶斯网络和马尔科夫随机场(Markov random fields)等方法,使用的思想是计算机科学中的离散数据结构可以快速编码、在包含成千上万个变量的高维空间操作概率分布。这些方法已经广泛应用于许多领域:网页搜索,医疗和故障诊断,图像理解,生物网络重建,语音识别,自然语言处理,高噪声环境下编码信息传输,机器人导航,等等。PGM框架为任何希望通过有限、含噪的观测来正确推理提供了必要的工具。
PGM最开始出现在计算机科学和人工智能领域,主要应用于医学诊断。假设一个医生正在给一个病人看病。从医生的角度,他掌握着病人相当数量的信息-诱因、症状、各种测试结果等。并且,他应当判断出,病人的病情诊断是什么,不同的质量方案会有什么样的反应等等。PGM的另外一个典型应用是图像分割。比如,我们有一张可能包含成千上万个像素。图像分割,就是给图像中每个像素贴上标签。例如下图所示,每个像素应该给贴上诸如草地、天空、牛或马此类类别标签。 
上述两个问题的共同点是:
1.它们都具有大量我们需要从中推理的变量。在图像分割问题中,不同的像素或者由像素构成的小区域的标签叫superpixels。
2.正确的结果具有不确定性,不管算法设计得如何清晰。
综上,PGM就是用来解决上述应用的框架。
模型是一个我们理解世界的形象化表示(Declarative representation)。如下图所示:

简单的讲,一个模型是一种我们理解周围世界的声明或者表达方式。在计算机内,一个模型包含我们对若干变量的理解,比如,这些变量是什么含义,变量之间如何交互。模型的这种特性使得我们能够将新的算法加入模型内部,同时加入新的外界知识。比如用专家只是知道模型,通过学习的方法改善模型等。
首先解释下不确定性(Uncertainty)。产生不确定性的原因主要有:
1、对世界认知状态的不完整;2、含有噪声的观测(Noisy observations);3、模型未能覆盖所有实际现象;4、固有的随机性;
概率论,通常具有清晰的表达式,强推理模式,可建立的学习方法
Graphical(图)来自计算机科学,是一种复杂数据结构。通常包括顶点和连接顶点的边。
最简单的图模型是贝叶斯网络,通常贝叶斯网络使用有向无环图来表示,图中的顶点表示随机变量,图中的边沿表示随机变量之间的概率依赖关系;在机器学习和图像处理中(图像分割)还经常使用马尔科夫网络(Markov network),通常马尔科夫网络使用无向图来表示顶点与周围顶点之间的关系。

下面给出一个在图像分割中实际应用的例子:

联合分布-在概率论中, 对两个随机变量X和Y,其联合分布是同时对于X和Y的概率分布.
对离散随机变量而言,联合分布概率密度函数为Pr(X = x & Y = y),即

因为是概率分布函数,所以必须有

以通过考试成绩评估学生学习情况为例。

I表示学生智力,可取值为0和1;D表示试卷难易程度,可取值为0和1;G代表最后的试卷结果等级,可取值为1,2,3。根据三个随机变量I,D,G的取值情况,我们知道三个随机变量一共有2*2*3种取值。联合分布P(I,D,G)的分布情况如上图右表所示。需要注意的一点是,I,D,G是相互独立的随机变量。
条件概率分布(条件分布)是现代概率论中的概念。已知两个相关的随机变量X 和Y,随机变量Y 在条件{X =x}下的条件概率分布是指当已知X 的取值为某个特定值x之时,Y 的概率分布。 如果Y 在条件{X =x}下的条件概率分布是连续分布,那么其密度函数称作Y 在条件{X =x}下的条件概率密度函数(条件分布密度、条件密度函数)。与条件分布有关的概念,常常以“条件”作为前缀,如条件期望、条件方差等等。
对于离散型的随机变量X
和Y(取值范围分别是 和
和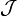 ),随机变量Y
在条件{X =x}下的条件概率分布是:
),随机变量Y
在条件{X =x}下的条件概率分布是:
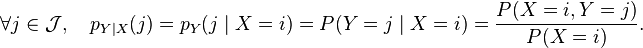 (
( )
)同样的,X 在条件{Y=y}下的条件概率分布是:
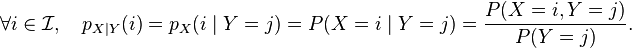 (
(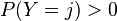 )
)其中,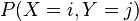 是X
和Y 联合分布概率,即“
是X
和Y 联合分布概率,即“ ,并且
,并且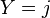 发生的概率”。如果用
发生的概率”。如果用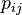 表示
表示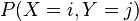 的值:
的值: 那么随机变量X 和Y 的边际分布就是:
那么随机变量X 和Y 的边际分布就是:

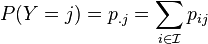
因此, 随机变量Y 在条件{X =x}下的条件概率分布也可以表达为:
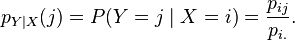 (
(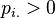 )
)同样的,X 在条件{Y=y}下的条件概率分布也可以表达为:
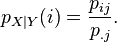 (
( )
)继续前面的例子,例如我们要求当G取值为1的时候的条件概率,那么P(I,D,G=1)为所有I和D变换,而G固定为1的联合分布的取值之和。

由上图我们知道,P(I,D,G=1)的值为0.126+0.009+0.252+0.06=0.447。这里G=1的条件概率不唯一,在实际应用中,使用条件概率时,常常还需要进行条件概率的归一化。简单的讲,就是在G=1的时候,可以将概率空间单纯的之前的3维(I,D,G各自所在的空间为一维)看做2维(G固定,只剩下I,D)。因此可条件概率的归一化是指条件概率的每一个可能的取值与条件概率之和的商。如下图,P(I,D|g=1)的条件概率分布如右表所示。

最后,还需要明确的一个概念是边缘概率。边缘概率是某个事件发生的概率。边缘概率是这样得到的:在联合概率中,把最终结果中不需要的那些事件合并成其事件的全概率而消失(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率)。这称为边缘化(marginalization)。A的边缘概率表示为P(A),B的边缘概率表示为P(B)。继续之前的例子,比如我们已经知道P(I,D|g=1),然后我们边缘化I,则我们可以得D的边缘分布,如下图所示:

标签:style http color 使用 strong 数据
原文地址:http://www.cnblogs.com/focus-ml/p/3698569.html