标签:erb mat 似然函数 参数估计 应该 原因 lam models 估计
对所有类型的CRF模型,包括最大熵模型,都是采用极大似然估计的方法来进行参数估计,也就是说在训练数据集$\mathcal T$上进行对数似然函数$\mathcal L$的极大化。根据上一篇《条件随机场(三)》,我们知道线性链CRF的模型为
\begin{equation} p_{\vec {\lambda}}(\vec y | \vec x) = \frac 1 {Z_{\vec {\lambda}} (\vec x)} exp(\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y_{j-1}, y_j, \vec x, j)) \end{equation}
\begin{equation} Z_{\vec {\lambda}}(\vec x) = \sum_{\vec {y} \in \mathcal Y} exp(\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y_{j-1}, y_j, \vec x, j)) \end{equation}
所以对数似然函数为,
\begin{equation} \begin{aligned} \overline {\mathcal L} (\mathcal T) & = \sum_{(\vec x, \vec y) \in \mathcal T} log p(\vec y | \vec x) \\ & = \sum_{(\vec x, \vec y) \in \mathcal T} [log (\frac {exp(\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y_{j-1}, y_j, \vec x, j))} { \sum_{y‘ \in \mathcal Y} exp(\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y‘_{j-1}, y‘_j, \vec x, j))})] \end{aligned} \end{equation}
为了避免过拟合,对数似然函数增加一个惩罚因子$- \sum_{i=1}^m \frac {\lambda_{i}^2} {2 \sigma^2}$,其中$\sigma^2$是平衡因子,于是重新组织对数似然函数并作变换,
\begin{equation} \begin{aligned} \mathcal {L} (\mathcal T) & = \sum_{(\vec x, \vec y) \in \mathcal T} [log (\frac {exp(\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y_{j-1}, y_j, \vec x, j))} { \sum_{y‘ \in \mathcal Y} exp(\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y‘_{j-1}, y‘_j, \vec x, j))})] - \sum_{i=1}^m \frac {\lambda_{i}^2} {2 \sigma^2} \\ & = \sum_{(\vec x, \vec y) \in \mathcal T} [(\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y_{j-1}, y_j, \vec x, j)) - log (\sum_{y‘ \in \mathcal Y} exp(\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y‘_{j-1}, y‘_j, \vec x, j)))] - \sum_{i=1}^m \frac {\lambda_{i}^2} {2 \sigma^2} \\ & = \underbrace {\sum_{(\vec x, \vec y) \in \mathcal T} \sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y_{j-1}, y_j, \vec x, j)}_{\mathcal A} \\ & \quad - \underbrace{\sum_{(\vec x, \vec y) \in \mathcal T} log \underbrace {(\sum_{y‘ \in \mathcal Y} exp(\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y‘_{j-1}, y‘_j, \vec x, j)))}_{Z_{\vec \lambda}(\vec x)}}_{\mathcal B} - \underbrace{\sum_{i=1}^m \frac {\lambda_{i}^2} {2 \sigma^2}}_{\mathcal C} \end{aligned}\end{equation}
对数似然函数$\mathcal L(\mathcal T)$的各项$\mathcal A, \mathcal B, \mathcal C$分别对$\lambda_i$求偏导,
\begin{equation} \frac \partial {\partial {\lambda_i}} \sum_{(\vec x, \vec y) \in \mathcal T} \sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i (y_{j-1}, y_j, \vec x, j) = \sum_{(\vec x, \vec y) \in \mathcal T} \sum_{j=1}^n f_j(y_{j-1}, y_j, \vec x, j) \end{equation}
上式的求导中,将$\lambda_i$看作变量,而$\lambda_k, k \neq i$看作常数。
\begin{equation} \begin{aligned} \frac \partial {\partial {\lambda_i}} \sum_{(\vec x, \vec y) \in \mathcal T} log Z_{\vec \lambda}(\vec x) & = \sum_{(\vec x, \vec y) \in \mathcal T} \frac 1 {Z_{\vec \lambda}(\vec x)} \frac {\partial {Z_{\vec \lambda}(\vec x)}} {\partial \lambda_j} \\ & = \sum_{(\vec x, \vec y) \in \mathcal T} \frac 1 {Z_{\vec \lambda}(\vec x)} \sum_{\vec {y}‘ \in \mathcal Y} exp (\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i ( y‘_{j-1}, y‘_j, \vec x , j)) \cdot \sum_{j=1}^n f_i(y‘_{j-1}, y‘_j, \vec x , j) \\ & = \sum_{(\vec x, \vec y) \in \mathcal T} \sum_{{\vec y}‘ \in \mathcal Y} \underbrace{\frac 1 {Z_{\vec \lambda}(\vec x)} exp(\sum_{j=1}^n \sum_{i=1}^m \lambda_i f_i ( y‘_{j-1}, y‘_j, \vec x , j))}_{=p_{\vec \lambda}(\vec y | \vec x)} \cdot \sum_{j=1}^n f_i(y‘_{j-1}, y‘_j, \vec x , j) \\ & = \sum_{(\vec x, \vec y) \in \mathcal T} \left( \sum_{{\vec y}‘ \in \mathcal Y} p_{\vec \lambda}({\vec y}‘ | \vec x) \sum_{j=1}^n f_i(y‘_{j-1}, y‘_j, \vec x , j) \right) \end{aligned} \end{equation}
\begin{equation} \frac \partial {\partial{\lambda_k}} (- \sum_{i=1}^m \frac {\lambda_{i}^2} {2 \sigma^2}) = - \frac {\lambda_k} {\sigma^2} \end{equation}
上面的对数似然函数(4)式是凹函数:其中第一项是线性的,因为关于$\lambda_i$求导后的表达式不包含$\lambda_i$了,第二项求导后的表达式中有一个归一化项,自然也与$\lambda_i$无关了,所以第二项也可以看成$\lambda_i$的线性项,而第三项明显是$\lambda_i$的凹函数,所以对数似然函数整体也是凹函数。
对数似然函数的$\mathcal A$项其实就是特征函数$f_i$在经验分布下的期望值(我怎么觉得要除以$| \mathcal T |$,然而这个对计算值没影响,后文会解释),
\begin{equation} \tilde{E}(f_i) = \sum_{(\vec x, \vec y) \in \mathcal T} \sum_{j=1}^n f_i (y_{j-1},y_j, \vec x, j) \end{equation}
$\mathcal B$项的求导则是CRF模型下的$f_i$的期望,
\begin{equation} \begin{aligned} E(f_i) & = \sum_{(\vec x, \vec y) \in \mathcal Z} p(\vec x, \vec y) \sum_{j=1}^n f_i ({y_{j-1}}‘ , {y_j}‘ , \vec x, j) \\ & = \sum_{(\vec x, \vec y) \in \mathcal Z} p(\vec x) p(\vec y | \vec x) \sum_{j=1}^n f_i ({y_{j-1}}‘ , {y_j}‘ , \vec x, j) \\ & = \sum_{(\vec x, \vec y) \in \mathcal Z} \tilde{p}(\vec x) p(\vec y | \vec x) \sum_{j=1}^n f_i ({y_{j-1}}‘ ,{y_j}‘ , \vec x, j) \\ & \propto \sum_{(\vec x, \vec y) \in \mathcal T} \sum_{{\vec y}‘ \in \mathcal Y} p_{\vec \lambda}({\vec y}‘ | \vec x) \sum_{j=1}^n f_i ({y_{j-1}}‘, {y_j}‘, \vec x, j) \end{aligned} \end{equation}
上式推导中使用经验概率$\tilde{p}(\vec x)$代替$p(\vec x)$,最后一步的正比其实就是乘以了训练集的数量$| \mathcal T|$,这与(8)式也是一致的,(8)中也是经验期望乘以了$| \mathcal T |$,而第三项也可以认为是经过了乘以$| \mathcal T |$ 这一步,
于是对数似然函数的偏导为,
\begin{equation} \frac {\partial {\mathcal {L} (\mathcal T)}} {\partial {\lambda_i}} = \tilde{E}(f_i) - E(f_i) - \frac {\lambda_i} {\sigma^2} \end{equation}
(8)和(9)式与最大熵模型(见条件随机场二中的(12)~(16)式)类似,令上式等于0,于是乘以的$| \mathcal T |$这一项就可以忽略了。
计算$f_i$的经验期望是很容易的,只要找出特征$f_i$在训练数据集中出现次数(按道理,应该除以$| \mathcal T |$,但是上文解释过了,可以忽略这一常数因子),计算$E(f_i)$则没那么容易了,因为分类序列的情况比较多,即$| \mathcal Y |$值比较大。而在最大熵模型中可以计算$E(f_i)$的原因是因为其分类输出为单个,而非一个序列,显然序列排序的情况比单个的情况多很多,比如分类总共有J个,则单个分类的情况就是J个,而n长度的序列的可能情况理论上则是 $J^n$个。在CRF中,由于计算的复杂,我们采用动态规划的方法,与HMM中一样,即前向-后向算法。如下图
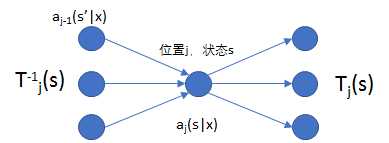
我们令$T_{j}(s)$表示从位置j,状态为s的节点出发可以到达下一个位置上所有状态对应的节点,$T{j}^{-1}(s)$表示位置 j 且状态为s的节点可以由上一个位置上所有可能的状态节点转换而来,根据前面HMM的介绍内容不难知道,对于线性链CRF模型,前向$\alpha$和后向$\beta$分别为,
\begin{equation} \alpha_{j}(s| \vec x) = \sum_{s‘ \in T_{j}^{-1}(s)} \alpha_{j-1}(s‘ | \vec x) \cdot \Psi_{j}(\vec x, s‘, s) \end{equation}
\begin{equation} \beta_{j}(s | \vec x) = \sum_{s‘ \in T_{j}(s)}(s‘ | \vec x) \cdot \Psi_{j}(\vec x, s, s‘) \end{equation}
其中势函数$\Psi_{j}(\vec x, s‘, s)$可以根据条件随机场(三)中的(3)式和(5)式很容易得到:$\Psi_{j}(\vec x, s, s‘) = \exp (\sum_{i=1}^m \lambda_i f_i (y_{j-1} = s, y_{j} = s‘ , \vec x , j)) $
这里,前向概率 $\alpha_{j}(s | \vec x)$表示输入为$\vec x$的条件下,位置 j 处的状态为 s 并且到位置 j 的前部分标记序列的非规范化条件概率,而后向概率 $\beta_{j}(s | \vec x)$ 表示输入为 $\vec x$的条件下,位置 j 的状态为s 且 j 位置到最后的那一部分标记序列的非规范化条件概率,一定要注意是非规范化的,因为没有考虑因子$Z_{\vec {\lambda}}(\vec x)$。
定义第一个位置 j = 1 之前的起始位置 j = 0 的状态记为 $\bot$,最后一个位置 j = n 之后的一个位置 j = n + 1 的状态记为 $\top$,于是有
\begin{equation} \alpha_{0} (\bot | \vec x) = 1 \end{equation}
\begin{equation} \beta_{|\vec x| + 1}(\top | \vec x) = 1 \end{equation}
有了上述信息,计算$f_i$的期望就可以有效地实现了,根据(9)式,
条件概率$\sum_{{\vec y}‘ \in \mathcal T} p_{\vec {\lambda}}({\vec y}‘ | \vec x)$表示给定输入$\vec x$的条件下,所有可能的输出$\vec y$的条件概率之和,易知
$$\sum_{{\vec y}‘ \in \mathcal T} p_{\vec {\lambda}}({\vec y}‘ | \vec x) = \frac 1 {Z_{\vec {\lambda}}(\vec x)} \sum_{s \in S} \alpha_{j}(s | \vec x) \beta_{j}(s|\vec x) $$
代入(9)式得,
\begin{equation} \begin{aligned} E(f_i) & = \sum_{(\vec x, \vec y) \in \mathcal T} \frac 1 {Z_{\vec {\lambda}}(\vec x)} \sum_{s \in S} \alpha_{j}(s | \vec x) \beta_{j}(s|\vec x) \cdot \sum_{j=1}^n f_i({y_{j-1}}‘, {y_j}‘, \vec x, j) \\ & = \sum_{(\vec x, \vec y) \in \mathcal T} \frac 1 {Z_{\vec {\lambda}}(\vec x)} \sum_{j=1}^n \sum_{s \in S} f_i({y_{j-1}}‘, {y_j}‘, \vec x, j) \alpha_{j}(s | \vec x) \beta_{j}(s|\vec x) \\ & = \sum_{(\vec x, \vec y) \in \mathcal T} \frac 1 {Z_{\vec {\lambda}}(\vec x)} \sum_{j=1}^n \sum_{s \in S} \sum_{s‘ \in T_{j}(s)} f_i((s, s‘, \vec x, j) \alpha_{j}(s | \vec x) \Psi_{j}(\vec x, s, s‘) \beta_{j+1}(s‘|\vec x) \end{aligned} \end{equation}
上式计算过程可以用下图形象的表示出来
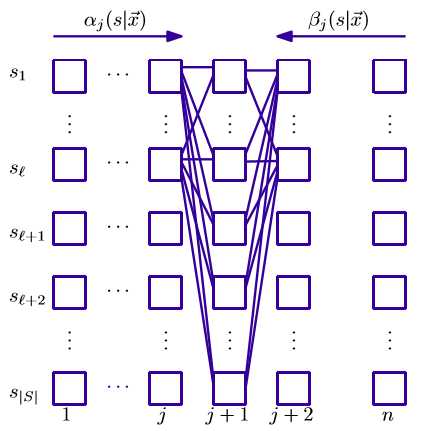
此外,归一化因子可以表示为
$$Z_{\vec {\lambda}}(\vec x) = \beta_{0}(\bot | \vec x) $$
于是解(10)式方程即可。
(未完待续,后面将持续统计学习相关的文章,鄙人也是边学边记录)
Classical Probabilistic Models and Conditional Random Fields
标签:erb mat 似然函数 参数估计 应该 原因 lam models 估计
原文地址:http://www.cnblogs.com/sjjsxl/p/7048564.html