标签:调整 ack style 提高 png 所有结点 com 二叉查找树 image
关于二叉树有一点需要注意:二叉树并不是树的一种特殊形式。
二叉树又有几种特殊的形式:二叉排序树(二叉查找树)、最优二叉树(哈弗曼树)、二叉堆(大顶堆,小顶堆)等。斜线是数据结构
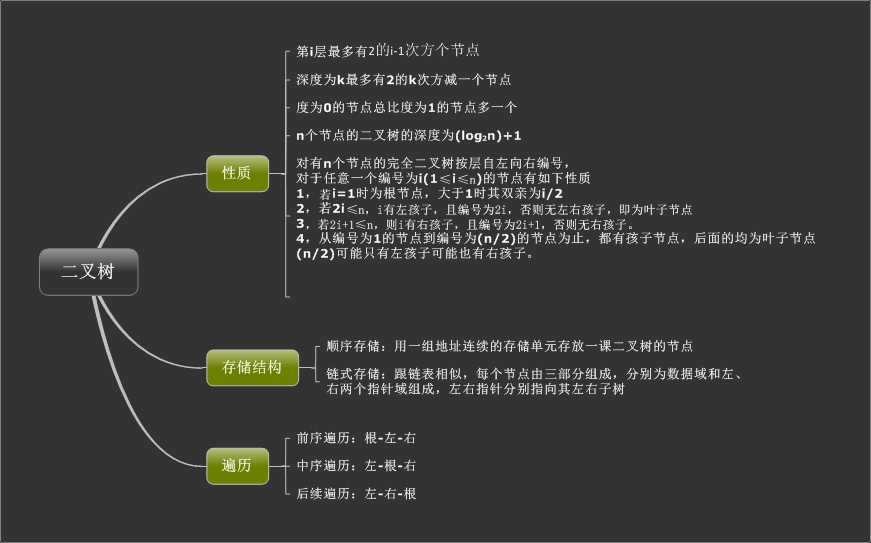
二叉排序树(二叉查找树)(BST)它或者是一棵空树;或者是具有下列性质的二叉树:(常用二分查找)
1,若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2,若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
3,左、右子树也分别为二叉排序树;
特有的性质:对于每个结点,左孩子均小于它,右孩子均大于它
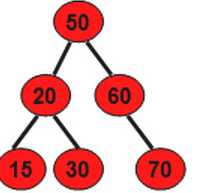
AVL树平衡二叉树
特有性质:第一:它是一颗二叉排序树,查找树,BST
第二:任何一个节点的左子树高度和右子树的高度差在-1,0,1三者之间
AVL树是一种自平衡二叉排序树,它的特点是任何一个节点的左子树高度和右子树的高度差在-1,0,1三者之间。AVL树的任何一个子树都是AVL树。
哈弗曼树特有性质:1.是一颗最普通的二叉树 2.就是带权路径长度最小,因此还叫最优二叉树。
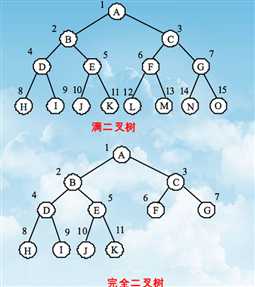
(1)完全二叉树——只有最下面的两层结点度小于2,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树;
(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶结点都处在最底层的二叉树,。
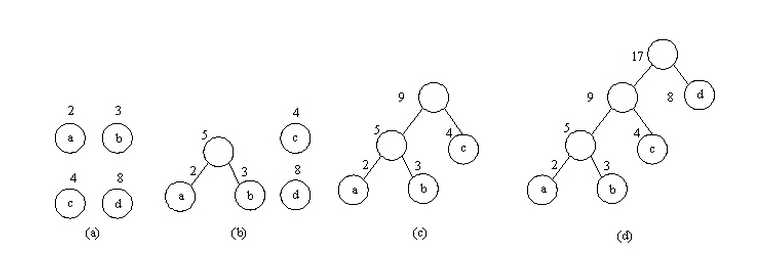
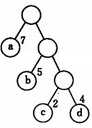
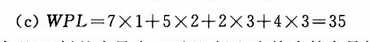
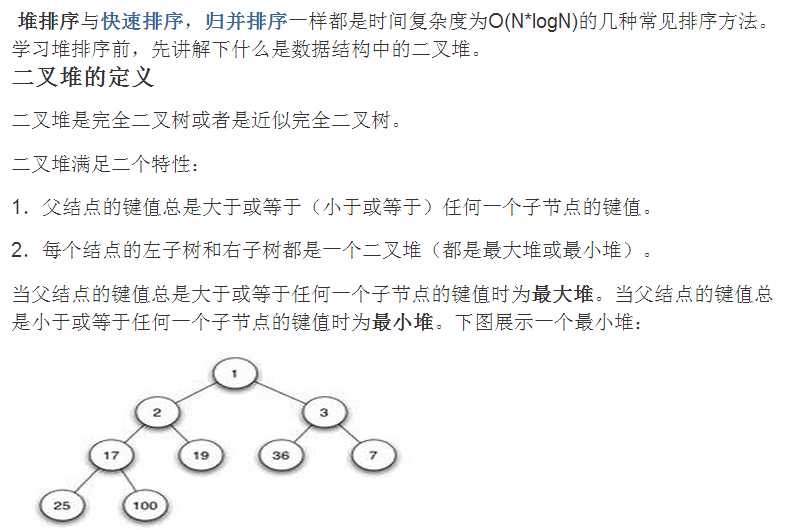
二叉堆分小顶堆和大顶堆:
性质:第一条,是一颗完全二叉树或者近似是一颗完全二叉树
第二条:任给一个结点总是>=其孩子的结点,部分左右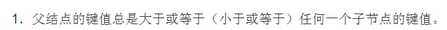
Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]或者Key[i]>=Key[2i+1]&&key>=key[2i+2]
即任何一非叶节点的关键字不大于或者不小于其左右孩子节点的关键字。
堆分为大顶堆和小顶堆,满足Key[i]>=Key[2i+1]&&key>=key[2i+2]称为大顶堆


完全二叉树是效率很高的数据结构,堆是一种完全二叉树或者近似完全二叉树,所以效率极高,像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化,几乎每次都要考到的二叉排序树的效率也要借助平衡性来提高,而平衡性基于完全二叉树。
堆排序:
 自底向上,自左向右进行调整为堆
自底向上,自左向右进行调整为堆
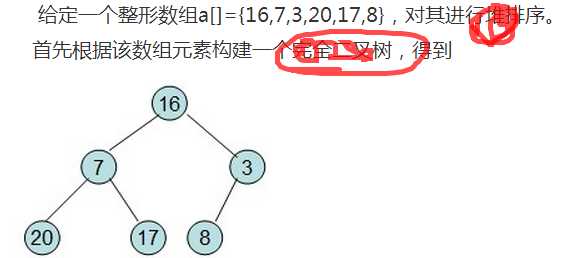
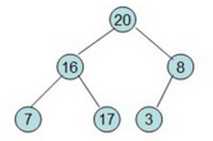
由一个完全二叉树到大顶堆
例子:调堆的过程应该从最后一个非叶子节点开始
分别与左孩子和右孩子比较大小,如果A[3]最大,则不用调整,否则和孩子中的值最大的一个交换位置,
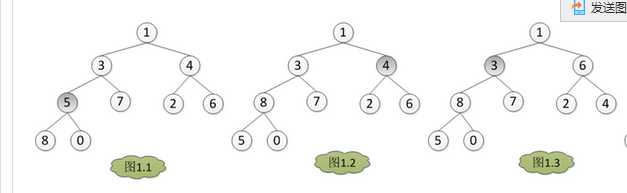
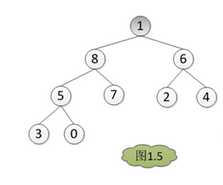
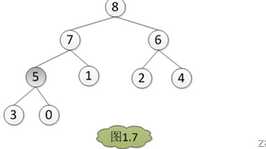
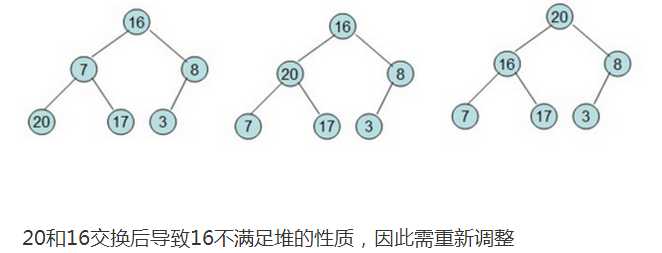
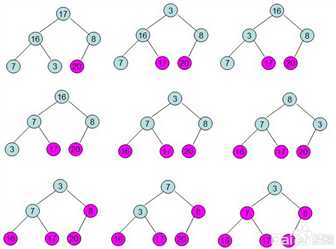
首先:最顶上那个元素和最末的那个元素交换
其次:调整为堆即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质,因此每次交换之后要重新对被交换的孩子节点进行调整)
最开始的这个堆,然后对这个堆进行排序
标签:调整 ack style 提高 png 所有结点 com 二叉查找树 image
原文地址:http://www.cnblogs.com/cs-lcy/p/7103656.html