标签:设计 ini 包括 空格 ring 下载软件 using 表示 fine
Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器,你可以通过一行命令安装某一个软件包,然后软件包管理器会帮助你从软件源下载软件包,同时自动解决所有的依赖(即下载安装这个软件包的安装所依赖的其它软件包),完成所有的配置。ebian/Ubuntu使用的apt-get,Fedora/CentOS使用的yum,以及OSX下可用的homebrew都是优秀的软件包管理器。
你决定设计你自己的软件包管理器。不可避免地,你要解决软件包之间的依赖问题。如果软件包A依赖软件包B,那么安装软件包A以前,必须先安装软件包B。同时,如果想要卸载软件包B,则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且,由于你之前的工作,除0号软件包以外,在你的管理器当中的软件包都会依赖一个且仅一个软件包,而0号软件包不依赖任何一个软件包。依赖关系不存在环(若有m(m≥2)个软件包A1,A2,A3,?,Am,其中A1依赖A2,A2依赖A3,A3依赖A4,……,A[m-1]依赖Am,而Am依赖A1,则称这m个软件包的依赖关系构成环),当然也不会有一个软件包依赖自己。
现在你要为你的软件包管理器写一个依赖解决程序。根据反馈,用户希望在安装和卸载某个软件包时,快速地知道这个操作实际上会改变多少个软件包的安装状态(即安装操作会安装多少个未安装的软件包,或卸载操作会卸载多少个已安装的软件包),你的任务就是实现这个部分。注意,安装一个已安装的软件包,或卸载一个未安装的软件包,都不会改变任何软件包的安装状态,即在此情况下,改变安装状态的软件包数为0。
输入格式:
从文件manager.in中读入数据。
输入文件的第1行包含1个整数n,表示软件包的总数。软件包从0开始编号。
随后一行包含n?1个整数,相邻整数之间用单个空格隔开,分别表示1,2,3,?,n?2,n?1号软件包依赖的软件包的编号。
接下来一行包含1个整数q,表示询问的总数。之后q行,每行1个询问。询问分为两种:
install x:表示安装软件包x
uninstall x:表示卸载软件包x
你需要维护每个软件包的安装状态,一开始所有的软件包都处于未安装状态。
对于每个操作,你需要输出这步操作会改变多少个软件包的安装状态,随后应用这个操作(即改变你维护的安装状态)。
输出格式:
输出到文件manager.out中。
输出文件包括q行。
输出文件的第i行输出1个整数,为第i步操作中改变安装状态的软件包数。
7 0 0 0 1 1 5 5 install 5 install 6 uninstall 1 install 4 uninstall 0
3 1 3 2 3
10 0 1 2 1 3 0 0 3 2 10 install 0 install 3 uninstall 2 install 7 install 5 install 9 uninstall 9 install 4 install 1 install 9
1 3 2 1 3 1 1 1 0 1
【样例说明 1】
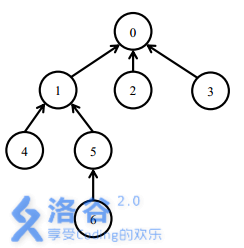
一开始所有的软件包都处于未安装状态。
安装5号软件包,需要安装0,1,5三个软件包。
之后安装6号软件包,只需要安装6号软件包。此时安装了0,1,5,6四个软件包。
卸载1号软件包需要卸载1,5,6三个软件包。此时只有0号软件包还处于安装状态。
之后安装4号软件包,需要安装1,4两个软件包。此时0,1,4处在安装状态。最后,卸载0号软件包会卸载所有的软件包。`
【数据范围】
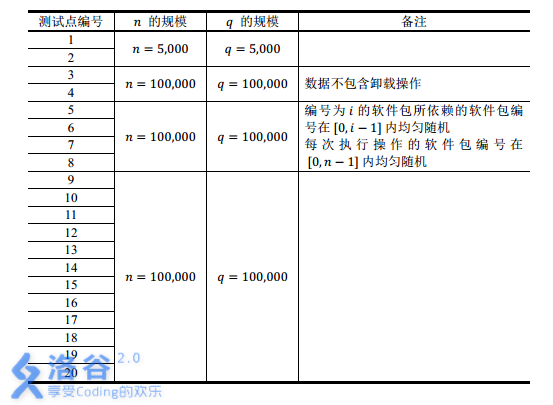
【时限1s,内存512M】
裸的树链剖分+线段树。树上(指题目给的树)每个结点有安装和未安装两种状态,对应计数1和0。树链剖分到线段树后,维护计数的和。
安装操作即把节点x到根的路径上所有节点的计数改为1,统计更改了多少节点并输出。
删除操作即把节点x及它的所有后代节点计数改为0,统计更改了多少节点并输出。
#include <iostream> #include <string> #include <vector> #define maxn 100010 using namespace std; int n, m; namespace seg { struct node { int ln, rn, mn; int len; int cnt, mark; }; node nds[maxn * 4]; void push_down(int p) { if (nds[p].mark != -1 && nds[p].len > 1) nds[p * 2].mark = nds[p * 2 + 1].mark = nds[p].mark; nds[p].mark = -1; } void pull_up(int p) { if (nds[p].mark != -1) nds[p].cnt = nds[p].mark * nds[p].len; else if (nds[p].len > 1) nds[p].cnt = nds[p * 2].cnt + nds[p * 2 + 1].cnt; } void init(int l, int r, int p = 1) { node &nd = nds[p]; nd.ln = l; nd.rn = r; nd.mn = (l + r) / 2; nd.len = r - l + 1; nd.cnt = 0; nd.mark = -1; if (l != r) { init(nd.ln, nd.mn, p * 2); init(nd.mn + 1, nd.rn, p * 2 + 1); } } void set(int l, int r, int val, int p = 1) { node &nd = nds[p]; if (nd.ln == l && nd.rn == r) { nd.mark = val; } else { push_down(p); if (l <= nd.mn) set(l, min(nd.mn, r), val, p * 2); else pull_up(p * 2); if (nd.mn + 1 <= r) set(max(l, nd.mn + 1), r, val, p * 2 + 1); else pull_up(p * 2 + 1); } pull_up(p); } int query(int l, int r, int p = 1) { node &nd = nds[p]; if (nd.mark != -1) { return nd.mark * (r - l + 1); } else if (nd.ln == l && nd.rn == r) { return nd.cnt; } else { int ans = 0; if (l <= nd.mn) ans += query(l, min(nd.mn, r), p * 2); if (nd.mn + 1 <= r) ans += query(max(l, nd.mn + 1), r, p * 2 + 1); return ans; } } } namespace tree { int parent[maxn]; vector<int> child[maxn]; void add_child(int p, int c) { parent[c] = p; child[p].push_back(c); } int depth[maxn], size[maxn], heavy[maxn]; void dfs1(int k = 0, int d = 0) { size[k] = 1; depth[k] = d; heavy[k] = -1; int max_size = 0; for (int i = 0; i < child[k].size(); ++i) { dfs1(child[k][i], d + 1); size[k] += size[child[k][i]]; if (max_size < size[child[k][i]]) { max_size = size[child[k][i]]; heavy[k] = child[k][i]; } } } int top[maxn], hash[maxn]; int cnt = 1; void dfs2(int k = 0) { hash[k] = cnt++; if (child[k].size()) { top[heavy[k]] = top[k]; dfs2(heavy[k]); for (int i = 0; i < child[k].size(); ++i) { if (child[k][i] != heavy[k]) { top[child[k][i]] = child[k][i]; dfs2(child[k][i]); } } } } int install(int k) { int ans = 0; while (true) { ans += (hash[k] - hash[top[k]] + 1) - seg::query(hash[top[k]], hash[k]); seg::set(hash[top[k]], hash[k], 1); if (top[k] == 0) break; k = parent[top[k]]; } return ans; } int uninstall(int k) { int ans = seg::query(hash[k], hash[k] + size[k] - 1); seg::set(hash[k], hash[k] + size[k] - 1, 0); return ans; } } int main() { cin >> n; int a; for (int i = 1; i <= n - 1; ++i) { cin >> a; tree::add_child(a, i); } tree::dfs1(); tree::dfs2(); seg::init(1, n); cin >> m; string str; while (m--) { cin >> str >> a; switch (str[0]) { case ‘i‘: cout << tree::install(a) << endl; break; case ‘u‘: cout << tree::uninstall(a) << endl; break; } } return 0; }
标签:设计 ini 包括 空格 ring 下载软件 using 表示 fine
原文地址:http://www.cnblogs.com/ssttkkl/p/7105610.html