标签：最优 star 操作 延伸 record limit sizeof cal 注意
直接暴力模拟，注意判数据结构为空时的取出操作。
1 #include<iostream> 2 #include<cstdio> 3 #include<ctime> 4 #include<cctype> 5 #include<cstring> 6 #include<cstdlib> 7 #include<fstream> 8 #include<sstream> 9 #include<algorithm> 10 #include<map> 11 #include<set> 12 #include<stack> 13 #include<queue> 14 #include<vector> 15 #include<stack> 16 using namespace std; 17 typedef bool boolean; 18 const signed int inf = (signed)((1u << 31) - 1); 19 #define smin(a, b) a = min(a, b) 20 #define smax(a, b) a = max(a, b) 21 #define max3(a, b, c) max(a, max(b, c)) 22 #define min3(a, b, c) min(a, min(b, c)) 23 template<typename T> 24 inline boolean readInteger(T& u){ 25 char x; 26 int aFlag = 1; 27 while(!isdigit((x = getchar())) && x != ‘-‘ && x != -1); 28 if(x == -1) { 29 ungetc(x, stdin); 30 return false; 31 } 32 if(x == ‘-‘){ 33 x = getchar(); 34 aFlag = -1; 35 } 36 for(u = x - ‘0‘; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - ‘0‘); 37 ungetc(x, stdin); 38 u *= aFlag; 39 return true; 40 } 41 42 int n; 43 stack<int> s; 44 queue<int> q; 45 priority_queue<int> que; 46 boolean prob[3] = {true, true, true}; 47 48 inline void solve() { 49 int opt, a, x; 50 readInteger(n); 51 while(n--) { 52 readInteger(opt); 53 readInteger(a); 54 if(opt == 1) { 55 if(prob[0]) s.push(a); 56 if(prob[1]) q.push(a); 57 if(prob[2]) que.push(a); 58 } else { 59 if(prob[0]) { 60 if(s.empty()) prob[0] = false; 61 else { 62 x = s.top();s.pop(); 63 if(x != a) prob[0] = false; 64 } 65 } 66 if(prob[1]) { 67 if(q.empty()) prob[1] = false; 68 else { 69 x = q.front();q.pop(); 70 if(x != a) prob[1] = false; 71 } 72 } 73 if(prob[2]) { 74 if(que.empty()) prob[2] = false; 75 else { 76 x = que.top();que.pop(); 77 if(x != a) prob[2] = false; 78 } 79 } 80 } 81 } 82 puts(prob[0] ? "YES" : "No"); 83 puts(prob[1] ? "YES" : "No"); 84 puts(prob[2] ? "YES" : "No"); 85 } 86 87 int main() { 88 freopen("qu.in", "r", stdin); 89 freopen("qu.out", "w", stdout); 90 solve(); 91 return 0; 92 }
考虑只有两个任务的时候，只有两种情况，它们的答案分别是
和
。又因为
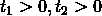,所以有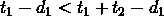
，
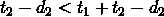，所以它们的谁更优取决于
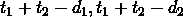。即d值的大小。
现在考虑多个任务的时候，先随便安排一种执行任务的顺序，如果存在有关d值的逆序对，那么说明当前这个顺序一定不优，我们可以通过交换相邻的一对逆序对使得结果更优。最优时即不存在有关d的逆序对吗，即按d值排序再计算答案就好了。
1 #include<iostream> 2 #include<cstdio> 3 #include<ctime> 4 #include<cctype> 5 #include<cstring> 6 #include<cstdlib> 7 #include<fstream> 8 #include<sstream> 9 #include<algorithm> 10 #include<map> 11 #include<set> 12 #include<stack> 13 #include<queue> 14 #include<vector> 15 #include<stack> 16 using namespace std; 17 typedef bool boolean; 18 const signed int inf = (signed)((1u << 31) - 1); 19 #define smin(a, b) a = min(a, b) 20 #define smax(a, b) a = max(a, b) 21 #define max3(a, b, c) max(a, max(b, c)) 22 #define min3(a, b, c) min(a, min(b, c)) 23 template<typename T> 24 inline boolean readInteger(T& u){ 25 char x; 26 int aFlag = 1; 27 while(!isdigit((x = getchar())) && x != ‘-‘ && x != -1); 28 if(x == -1) { 29 ungetc(x, stdin); 30 return false; 31 } 32 if(x == ‘-‘){ 33 x = getchar(); 34 aFlag = -1; 35 } 36 for(u = x - ‘0‘; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - ‘0‘); 37 ungetc(x, stdin); 38 u *= aFlag; 39 return true; 40 } 41 42 typedef class Task { 43 public: 44 int t; 45 int d; 46 47 Task(int t = 0, int d = 0):t(t), d(d) { } 48 49 boolean operator < (Task b) const { 50 if(d != b.d) return d < b.d; 51 return t < b.t; 52 } 53 }Task; 54 55 int n; 56 Task* ts; 57 58 inline void init() { 59 readInteger(n); 60 ts = new Task[(const int)(n + 1)]; 61 for(int i = 1; i <= n; i++) { 62 readInteger(ts[i].t); 63 readInteger(ts[i].d); 64 } 65 } 66 67 int res = 0; 68 inline void solve() { 69 sort(ts + 1, ts + n + 1); 70 int fin = 0; 71 for(int i = 1; i <= n; i++) { 72 fin += ts[i].t; 73 smax(res, max(0, fin - ts[i].d)); 74 } 75 printf("%d\n", res); 76 } 77 78 int main() { 79 freopen("ming.in", "r", stdin); 80 freopen("ming.out", "w", stdout); 81 init(); 82 solve(); 83 return 0; 84 }
先说一下70分做法(由于数据比较水，所以暴力基本上可以过7个点)吧。
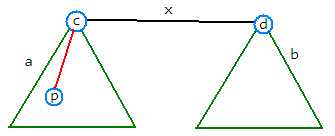
我在考试的时候用的是方法1。
1 #include<iostream> 2 #include<cstdio> 3 #include<ctime> 4 #include<cctype> 5 #include<cstring> 6 #include<cstdlib> 7 #include<fstream> 8 #include<sstream> 9 #include<algorithm> 10 #include<map> 11 #include<set> 12 #include<stack> 13 #include<queue> 14 #include<vector> 15 #include<stack> 16 using namespace std; 17 typedef bool boolean; 18 const signed int inf = (signed)((1u << 31) - 1); 19 #define smin(a, b) a = min(a, b) 20 #define smax(a, b) a = max(a, b) 21 #define max3(a, b, c) max(a, max(b, c)) 22 #define min3(a, b, c) min(a, min(b, c)) 23 template<typename T> 24 inline boolean readInteger(T& u){ 25 char x; 26 int aFlag = 1; 27 while(!isdigit((x = getchar())) && x != ‘-‘ && x != -1); 28 if(x == -1) { 29 ungetc(x, stdin); 30 return false; 31 } 32 if(x == ‘-‘){ 33 x = getchar(); 34 aFlag = -1; 35 } 36 for(u = x - ‘0‘; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - ‘0‘); 37 ungetc(x, stdin); 38 u *= aFlag; 39 return true; 40 } 41 42 ///map template starts 43 typedef class Edge{ 44 public: 45 int end; 46 int next; 47 int w; 48 Edge(const int end = 0, const int next = 0, const int w = 0):end(end), next(next), w(w){} 49 }Edge; 50 51 typedef class MapManager{ 52 public: 53 int ce; 54 int *h; 55 Edge *edge; 56 MapManager(){} 57 MapManager(int points, int limit):ce(0){ 58 h = new int[(const int)(points + 1)]; 59 edge = new Edge[(const int)(limit + 1)]; 60 memset(h, 0, sizeof(int) * (points + 1)); 61 } 62 inline void addEdge(int from, int end, int w){ 63 edge[++ce] = Edge(end, h[from], w); 64 h[from] = ce; 65 } 66 inline void addDoubleEdge(int from, int end, int w){ 67 addEdge(from, end, w); 68 addEdge(end, from, w); 69 } 70 Edge& operator [] (int pos) { 71 return edge[pos]; 72 } 73 }MapManager; 74 #define m_begin(g, i) (g).h[(i)] 75 ///map template ends 76 77 const int moder = 1e9 + 7; 78 79 int n; 80 MapManager *g; 81 int* siz; 82 int s[100005]; // The size of node i. 83 int fs[100005]; // The length of a edge which connects node i and its father node. 84 85 inline int mod_plus(int a, int b) { 86 int ret = a + b; 87 while(ret >= moder) ret -= moder; 88 return ret; 89 } 90 91 inline void init() { 92 readInteger(n); 93 g = new MapManager[(const int)(n + 1)]; 94 siz = new int[(const int)(n + 1)]; 95 siz[0] = 1; 96 g[0] = MapManager(1, 0); 97 } 98 99 int cnt = 0; 100 inline void mknewtree(int a, int b, int c, int d, int l) { // Make a new tree following the recipe within O(n). 101 cnt++; 102 siz[cnt] = siz[a] + siz[b]; 103 g[cnt] = MapManager(siz[cnt], siz[cnt] << 1); 104 for(int i = 0; i < siz[a]; i++) 105 for(int j = m_begin(g[a], i); j; j = g[a][j].next) 106 g[cnt].addEdge(i, g[a][j].end, g[a][j].w); 107 for(int i = 0; i < siz[b]; i++) 108 for(int j = m_begin(g[b], i); j; j = g[b][j].next) 109 g[cnt].addEdge(i + siz[a], g[b][j].end + siz[a], g[b][j].w); 110 g[cnt].addDoubleEdge(c, d + siz[a], l); 111 } 112 113 int res = 0; 114 void calcLength(int node, int fa) { 115 s[node] = 1; 116 for(int i = m_begin(g[cnt], node); i; i = g[cnt][i].next) { 117 int& e = g[cnt][i].end; 118 if(e == fa) continue; 119 fs[e] = g[cnt][i].w; 120 calcLength(e, node); 121 s[node] += s[e]; 122 } 123 res = mod_plus(res ,(s[node] * 1LL * (siz[cnt] - s[node]) * fs[node]) % moder); 124 } 125 126 inline void solve() { 127 int a, b, c, d, l; 128 while(n--) { 129 readInteger(a); 130 readInteger(b); 131 readInteger(c); 132 readInteger(d); 133 readInteger(l); 134 mknewtree(a, b, c, d, l); 135 res = 0, fs[0] = 0; 136 calcLength(0, -1); 137 printf("%d\n", res); 138 } 139 } 140 141 int main() { 142 freopen("zi.in", "r", stdin); 143 freopen("zi.out", "w", stdout); 144 init(); 145 solve(); 146 return 0; 147 }
方法1似乎无法优化了，但是方法2很有搞头，因为不用建树。你可以试试人工模拟几组数据，然后你会惊讶地发现真正的状态数并不多，大概也就O(m2)吧，对于树上任意两点的距离，也就顶多连接点的组合，而这些点的（不同树上的总共）个数都是O(m)的。而考虑树上一棵树到其任意一点的距离总和，也就是到的都是连接点，数量也不多。因此2个map强势登场一堆记忆化加上直接把这道题水掉了。。
如果还不清楚就结合代码看吧。
1 #include<iostream> 2 #include<cstdio> 3 #include<ctime> 4 #include<cctype> 5 #include<cstring> 6 #include<cstdlib> 7 #include<fstream> 8 #include<sstream> 9 #include<algorithm> 10 #include<map> 11 #include<set> 12 #include<stack> 13 #include<queue> 14 #include<vector> 15 #include<stack> 16 #ifndef WIN32 17 #define Auto "%lld" 18 #else 19 #define Auto "%I64d" 20 #endif 21 using namespace std; 22 typedef bool boolean; 23 const signed int inf = (signed)((1u << 31) - 1); 24 #define smin(a, b) a = min(a, b) 25 #define smax(a, b) a = max(a, b) 26 #define max3(a, b, c) max(a, max(b, c)) 27 #define min3(a, b, c) min(a, min(b, c)) 28 template<typename T> 29 inline boolean readInteger(T& u){ 30 char x; 31 int aFlag = 1; 32 while(!isdigit((x = getchar())) && x != ‘-‘ && x != -1); 33 if(x == -1) { 34 ungetc(x, stdin); 35 return false; 36 } 37 if(x == ‘-‘){ 38 x = getchar(); 39 aFlag = -1; 40 } 41 for(u = x - ‘0‘; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - ‘0‘); 42 ungetc(x, stdin); 43 u *= aFlag; 44 return true; 45 } 46 47 #define LL long long 48 49 template<typename T1, typename T2> 50 inline pair<T1, T2> mkpair(T1 a, T2 b) { 51 return pair<T1, T2>(a, b); 52 } 53 54 const LL moder = 1e9 + 7; 55 56 LL n; 57 LL *a, *b, *l; 58 LL *c, *d; 59 LL* siz; 60 LL* res; 61 62 inline LL mod_plus(LL a, LL b) { 63 LL ret = a + b; 64 // while(ret >= moder) ret -= moder; 65 return ret % moder; 66 } 67 68 inline void init() { 69 readInteger(n); 70 siz = new LL[(const LL)(n + 1)]; 71 siz[0] = 1; 72 a = new LL[(const LL)(n + 1)]; 73 b = new LL[(const LL)(n + 1)]; 74 c = new LL[(const LL)(n + 1)]; 75 d = new LL[(const LL)(n + 1)]; 76 l = new LL[(const LL)(n + 1)]; 77 res = new LL[(const LL)(n + 1)]; 78 for(LL i = 1; i <= n; i++) { 79 readInteger(a[i]); 80 readInteger(b[i]); 81 readInteger(c[i]); 82 readInteger(d[i]); 83 readInteger(l[i]); 84 siz[i] = siz[a[i]] + siz[b[i]]; 85 } 86 } 87 88 map<pair<LL, pair<LL, LL> >, LL> dis; // Records the distance between node u and node v in tree tr. 89 map<pair<LL, LL>, LL> D; // Records 90 91 LL length(LL tr, LL u, LL v) { // Calculate the distance from node u to node v 92 if(tr == 0) return 0; 93 pair<LL, pair<LL, LL> > key = mkpair(tr, mkpair(u, v)); 94 if(dis.count(key)) return dis[key]; 95 LL ls = siz[a[tr]]; 96 LL ret; 97 if(u < ls && v < ls) ret = length(a[tr], u, v); 98 else if(u >= ls && v >= ls) ret = length(b[tr], u - ls, v - ls); 99 else { 100 if(u > v) swap(u, v); 101 ret = mod_plus(mod_plus(length(a[tr], u, c[tr]), l[tr]), length(b[tr], v - ls, d[tr])); 102 } 103 return dis[key] = ret; 104 } 105 106 LL calc(LL tr, LL p) { // Calculate the distance from all the nodes in tree tr to node p in tree tr 107 if(tr == 0) return 0; 108 pair<LL, LL> key = mkpair(tr, p); 109 if(D.count(key)) return D[key]; 110 LL ls = siz[a[tr]]; 111 LL ret; 112 if(p < ls) { // Node p is in tree a[tr]. 113 ret = (length(tr, d[tr] + ls, p) * 1LL * siz[b[tr]]) % moder; 114 ret = mod_plus(ret, calc(a[tr], p)); 115 ret = mod_plus(ret, calc(b[tr], d[tr])); 116 } else { // Otherwise node p is in tree b[tr]. 117 ret = (length(tr, c[tr], p) * 1LL * siz[a[tr]]) % moder; 118 ret = mod_plus(ret, calc(a[tr], c[tr])); 119 ret = mod_plus(ret, calc(b[tr], p - ls)); 120 } 121 return D[key] = ret; 122 } 123 124 inline void solve() { 125 res[0] = 0; 126 for(LL i = 1; i <= n; i++) { 127 res[i] = mod_plus(((siz[a[i]] % moder) * 1LL * (siz[b[i]] % moder) % moder * 1LL * l[i]) % moder, mod_plus(res[a[i]], res[b[i]])); 128 LL x = calc(a[i], c[i]); 129 LL y = calc(b[i], d[i]); 130 res[i] = mod_plus(mod_plus(res[i], (x * siz[b[i]]) % moder), (y * siz[a[i]])); 131 } 132 for(LL i = 1; i <= n; i++) 133 printf(Auto"\n", res[i]); 134 } 135 136 int main() { 137 freopen("zi.in", "r", stdin); 138 freopen("zi.out", "w", stdout); 139 init(); 140 solve(); 141 return 0; 142 }
NOIP模拟题 2017.7.3 - 模拟 - 贪心 - 记忆化搜索
标签：最优 star 操作 延伸 record limit sizeof cal 注意
原文地址：http://www.cnblogs.com/yyf0309/p/7112499.html
