标签:oppo ubi lisp -o 积分 sign 表达式 报错 读书
人们对功能强大的程序语言设计有一个要求,就是能为公共的模式命名,建立抽象,而后在抽象的层次上工作。我们需要构造以过程为参数或返回值的过程。
我们考虑计算一个函数term从a到b的和的过程:
(define(sum term a next b)
(if (> a b)
0
(+ (term a)
(sum term (next a) b))))
我们可以利用这个过程求立方和,或者计算定积分等,下面是计算定积分的代码:
(define (integral f a b dx)
(define (add-dx x) (+ x dx))
(* (sum f (+ a (/ dx 2.0)) add-dx b)
dx))
代码如下
(define (Simpson-integral f a b n)
(define h (/ (- b a) (* n 1.0)))
(define (is-odd? x)
(= (remainder x 2) 1))
(define (Simpson-sum k)
(cond ((= k 0) (+ (f a) (Simpson-sum (+ k 1))))
((= k n) (f b))
((is-odd? k) (+ (* 4 (f (+ a (* k h)))) (Simpson-sum (+ k 1))))
(else (+ (* 2 (f (+ a (* k h)))) (Simpson-sum (+ k 1))))))
(* (/ h 3) (Simpson-sum 0)))
经计算,结果确实得到了更高的精度。
补充完整的代码如下:
(define (sum term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (+ (term a) result))))
(iter a 0))
(a)代码如下
(define (product term a next b)
(if (> a b)
1
(* (term a) (product term (next a) next b))))
(define (cal-pi n)
(define (inc x)
(+ x 1))
(define (f x)
(/ (* 4 x (+ x 1)) (* (+ 1 (* 2 x)) (+ 1 (* 2 x)))))
(* 4.0 (product f 1 inc n)))
(b)product 的迭代形式的代码如下
(define (product term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (* (term a) result))))
(iter a 1))
(a)代码如下
(define (accumulate combiner null-value term a next b)
(if (> a b)
null-value
(combiner (term a)
(accumulate combiner null-value term (next a) next b))))
(b)迭代形式的代码如下
(define (accumulate combiner null-value term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (combiner a result))))
(iter a null-value))
和前面的练习并无本质区别,略去。
一般而言,lambda用于define同样的方式创造过程,除了不为有关过程提供名字以外。
主要注意以下两点:
(+ (let ((x 3))
(+ x (* x 10)))
x)
值就是38。
(let ((x 3)
(y (+ x 2)))
(* x y))
值为12,因为这里的y值将会为4。
这时解释器会试图求(f 2),那么这将导致解释器试图求(2 2),由于2不是一个过程,所以这将导致解释器报错。
这个原理比较简单,不多赘述,下面是实现这一过程的代码:
(define (search f neg-point pos-point)
(let ((midpoint (average neg-point pos-point)))
(if (close-enough? neg-point pos-point)
midpoint
(let ((test-value (f midpoint)))
(cond ((positive? test-value)
(search f neg-point midpoint))
((negative? test-value)
(search f midpoint pos-point))
(else midpoint))))))
(define (half-interval-method f a b)
(let ((a-value (f a))
(b-value (f b)))
(cond ((and (negative? a-value) (positive? b-value))
(search f a b))
((and (positive? a-value) (negative? b-value))
(search f b a))
(else
(error "Values are not of opposite sign" a b)))))
我们通过对一个初始值反复作用f,来得到不动点的一个近似值
(define tolerance 0.00001)
(define (fix-point f first-guess)
(define (close-enough? x y)
(< (abs (- x y)) tolerance))
(define (try guess)
(let ((next (f guess)))
(if (close-enough? guess next)
next
(try next))))
(try first-guess))
求平方根也可化为求函数的不动点问题,因为y平方根事实上是函数y/x的不动点,但是我们不能直接利用上面的方法,而需要做一点小小的改动。如果直接用上面的方法,容易看出我们的序列将会在x和y/x两个值之间不停振荡,无法收敛到不动点。 因此,我们为了使振荡不过于剧烈,取下一个猜测为1/2(y + y/x),这和我们在1.1.7节中所用的方法是一致的,这是一种被称为平均阻尼的技术,它常常用在不动点搜寻中,作为帮助收敛的手段。
利用这件事,求得的Φ的值为
1.6180327868852458
未使用平均阻尼时计算了34步,当使用平均阻尼时,仅用了9步就达到了要求的精度。
(a)当k取11的时候,能达到4位精度,代码如下:
(define (cont-frac n d k)
(define (cal i)
(if (= i k)
(/ (n k) (d k))
(/ (n i) (+ (d i) (cal (+ i 1))))))
(cal 1))
(b)代码如下:
(define (cont-frac n d k)
(define (iter-cal i res)
(if (= i 0)
res
(iter-cal (- i 1) (/ (n i) (+ (d i) res)))))
(iter-cal k 0))
代码如下:
(define (euler-e k)
(define (div a b)
(/ (- a (remainder a b)) b))
(cont-frac (lambda (i) 1.0)
(lambda (i) (cond ((= (remainder i 3) 0) 1)
((= (remainder i 3) 1) 1)
((= (remainder i 3) 2)
(* 2 (+ 1 (div i 3))))))
k))
代码如下:
(define (tan-cf x k)
(cont-frac (lambda (i) (if (= i 1)
x
(- (square x))))
(lambda (i) (- (* 2 i) 1))
k))
通过把过程作为返回值,我们可以把平均阻尼定义为下面的过程:
(define (average-damp f) (lambda (x) (average x (f x))))
这将会返回一个过程,过程在x处的取值为(f(x)+x)/2。利用平均阻尼,我们可以重新定义平方根过程如下:
(define (sqrt x)
(fixed-point (average-damp (lambda (y) (/ x y)))
1.0))
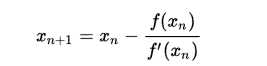
牛顿法的公式如上所述,为了能够方便地写出牛顿法的程序,我们先定义导数:
(define (deriv g)
(lambda (x)
(/ (- (g (+ x dx)) (g x))
dx)))
然后定义了dx之后,我们便可以使用deriv过程为函数求导,于是我们可以如下定义牛顿法:
(define (newton-transform g)
(lambda (x)
(- x (/ (g x) ((deriv g) x)))))
(define (newtons-method g guess)
(fixed-point (newton-transform g) guess))
利用牛顿法,我们还可以用另一种方式写出求平方根的方法:
(define (sqrt x)
(newtons-method (lambda (y) (- (square y) x))
1.0))
求平方根的两种方法事实上都是从一个函数出发,找出这一函数在某种变换下的不动点,我们将这一普遍的思想写成下面的函数:
(define (fixed-point-of-transform g transform guess) (fixed-point (transform g) guess))
Lisp是一个给了过程一级状态的语言,这给有效实现提出了挑战,但是由此获得了惊人的描述能力。
代码如下:
(define (cubic a b c) (lambda (x) (+ (cube x) (* a (square x)) (* b x) c)))
代码如下:
(define (double f) (lambda (x) (f (f x))))
该表达式,将返回21。
代码如下:
(define (compose f g) (lambda (x) (f (g x))))
代码如下:
(define (repeated f n)
(if (= n 0)
(lambda (x) x)
(compose f (repeated f (- n 1)))))
代码如下:
(define (smooth f)
(lambda (x) (/ (+ (f (- x dx)) (f x) (f (+ x dx)))
3)))
经试验,n次方根所需的平均阻尼为log2(n)次,为此写出代码如下:
(define (nth-root a n)
(define (log2 x)
(if (< x 2)
0
(+ 1 (log2 (/ x 2)))))
(let ((h (log2 n)))
(fixed-point ((repeated average-damp h) (lambda (x) (/ a (pow x (- n 1)))))
1.0)))
代码如下:
(define (iterative-improve judge improve)
(define (sol guess)
(if (judge guess)
(improve guess)
(sol (improve guess))))
(lambda (x) (sol x)))
重写后的sqrt与fixed-point如下:
(define (sqrt a)
((iterative-improve (lambda (guess) (< (abs (- (square guess) a)) 0.001))
(lambda (guess) (average guess (/ a guess)))) a))
(define (fixed-point f guess)
((iterative-improve (lambda (guess) (< (abs (- guess (f guess))) tolerance))
(lambda (guess) (f guess))) guess))
标签:oppo ubi lisp -o 积分 sign 表达式 报错 读书
原文地址:http://www.cnblogs.com/mhkds/p/7082371.html