标签:site turn zjoi2006 images 思路 code ccf str das
物流公司要把一批货物从码头A运到码头B。由于货物量比较大,需要n天才能运完。货物运输过程中一般要转停好几个码头。物流公司通常会设计一条固定的运输路线,以便对整个运输过程实施严格的管理和跟踪。由于各种因素的存在,有的时候某个码头会无法装卸货物。这时候就必须修改运输路线,让货物能够按时到达目的地。但是修改路线是—件十分麻烦的事情,会带来额外的成本。因此物流公司希望能够订一个n天的运输计划,使得总成本尽可能地小。
输入格式:
第一行是四个整数n(l≤n≤100)、m(l≤m≤20)、K和e。n表示货物运输所需天数,m表示码头总数,K表示每次修改运输路线所需成本。接下来e行每行是一条航线描述,包括了三个整数,依次表示航线连接的两个码头编号以及航线长度(>0)。其中码头A编号为1,码头B编号为m。单位长度的运输费用为1。航线是双向的。再接下来一行是一个整数d,后面的d行每行是三个整数P(1<P<m),a,b(1≤a≤b≤n)。表示编号为P的码头从第a天到第b天无法装卸货物(含头尾)。同一个码头有可能在多个时间段内不可用。但任何时间都存在至少一条从码头A到码头B的运输路线。
输出格式:
包括了一个整数表示最小的总成本。总成本=n天运输路线长度之和+K*改变运输路线的次数。
5 5 10 8 1 2 1 1 3 3 1 4 2 2 3 2 2 4 4 3 4 1 3 5 2 4 5 2 4 2 2 3 3 1 1 3 3 3 4 4 5
32
【样例输入说明】
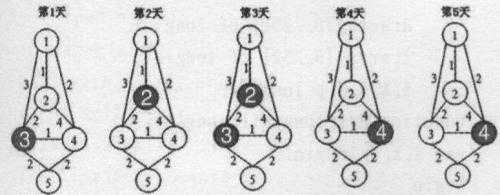
上图依次表示第1至第5天的情况,阴影表示不可用的码头。
【样例输出说明】
前三天走1-4-5,后两天走1-3-5,这样总成本为(2+2)*3+(3+2)*2+10=32。
_NOI导刊2010提高(01)
思路:
首先如果你每次都选取能够走的最短路时,它加起来就不一定会是最短的,为什么呢?
因为如果更改路径的话一次要加k,如果你更改之后的值+k后小于不更改路线的值,是很亏的.
所以我们需要用动态规划来做这道题目
坑点:
1.要看好spfa过程中队列q是为空还是不为空
2.一定要注意开数组的范围
3.要注意循环到什么,是n还是m.
上代码:
#include <iostream> #include <cstring> #include <cstdio> #include <cmath> #include <queue> using namespace std; const int M = 23; const int N = 123; const int INF = 1e8; int n,m,k,E,d,tot; bool cannot[M][N],visited[M]; int head[M],dis[M]; int cost[N][N],dp[N]; int ans; struct A{ int next,to,w; }e[1234]; queue<int>q; void add(int u,int v,int w) { e[++tot].to=v; e[tot].w=w; e[tot].next=head[u]; head[u]=tot; } bool pd(int Now,int l,int r) { for(int i=l;i<=r;i++) if(cannot[Now][i]) return false; return true; } int spfa(int l,int r) { if(!pd(1,l,r)) return INF; memset(visited,0,sizeof(visited)); for(int i=1;i<=m;i++) dis[i]=INF; while(!q.empty()) q.pop(); q.push(1); visited[1]=true; dis[1]=0; while(!q.empty()) { int u=q.front(); q.pop(); for(int i=head[u];i;i=e[i].next) { int w=e[i].w; int v=e[i].to; if(!pd(v,l,r)) continue; if(dis[v]>dis[u]+w) { dis[v]=dis[u]+w; if(!visited[v]) { q.push(v); visited[v]=true; } } } visited[u]=false; } if(dis[m]==INF) return INF; else return dis[m]*(r-l+1); } int main() { scanf("%d%d%d%d",&n,&m,&k,&E); for(int i=1,a,b,c;i<=E;i++) { scanf("%d%d%d",&a,&b,&c); add(a,b,c),add(b,a,c); } scanf("%d",&d); for(int i=1,P,a,b;i<=d;i++) { scanf("%d%d%d",&P,&a,&b); for(int j=a;j<=b;j++) cannot[P][j]=true; } ///寻找从i到j能够不改变路径的最短距离 for(int i=1;i<=n;i++) for(int j=i;j<=n;j++) cost[i][j]=spfa(i,j); dp[0]=0; ///将dp数组赋值为从开始到达当前的能够行走的最短距离 for(int i=1;i<=n;i++) dp[i]=cost[1][i]; for(int i=2;i<=n;i++) for(int j=i-1;j>=1;j--) { if(cost[j+1][i]!=INF) dp[i]=min(dp[i],dp[j]+cost[j+1][i]+k); ///因为是逆序枚举,所以如果当前j是没有被更新的(为INF), ///那么之前的也一定不会被更新,所以直接break掉就好 else break; } ///到第n天的最小花费 printf("%d\n",dp[n]); return 0; }
标签:site turn zjoi2006 images 思路 code ccf str das
原文地址:http://www.cnblogs.com/zxqxwnngztxx/p/7113033.html