标签:kd-tree read ttl open height alt png 复杂度 网上
然而今天在做另一道题时回想起了这道题,发现时间复杂度并不能证明为$O(n\log n)$或$O(n\sqrt n)$。
然后仔细一想竟然发现时间复杂度是$O(n^2)$的?!
该题题解为KD-tree,然而事实上这样分割矩形的方法是非常不科学的,于是出了一组数据卡掉了它。
原题中要求的是ax+by<c的,即在ax+by-c=0这条直线以下的所有点的权值之和。那么只要让直线穿过所有矩形即可。
然后有了右图的思路: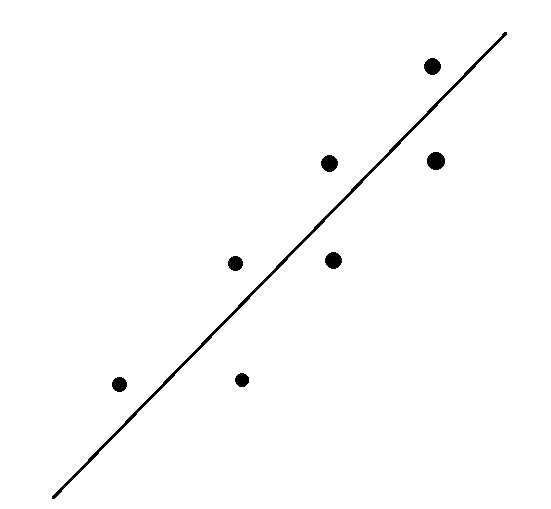
这样建树的中序遍历就是从左下到右上的顺序,而这里面任意两个点构成的矩形均被直线所穿过。这样一来每次查询都需要查询整棵树,从而时间复杂度退化到$O(n^2)$。
数据生成器:
#include <cstdio>
int main()
{
freopen("data.in" , "w" , stdout);
int n = 50000 , m = 50000 , i;
printf("%d %d\n" , n , m);
for(i = 1 ; i <= n ; i ++ )
printf("%d %d 1\n" , i / 2 * 2 , (i + 1) / 2 * 2 - 1);
for(i = 1 ; i <= m ; i ++ ) printf("1 -1 0\n");
return 0;
}
然后博主本人做了一个小实验,把网上的标程都复制粘贴下来,使用Lemon,时间限制10s,内存限制512MB并开启O2开关进行评测。
结果通过率为0%
结果如下:
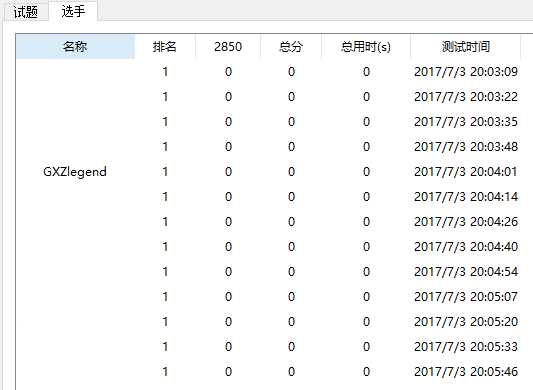

(这里为保护其他人隐私,将别人的名称涂掉了,只留下尴尬的爆零的博主)。
所以说本题正解一定不是KD-tree!(正解被Hack掉了)
那么正解究竟是什么?
其实博主也很好奇,但是网上的题解全都是被卡掉了的KD-tree,于是在这里真心求正解。
希望知道正解的好心人能够将题解发给博主,博主将万分感激!
另附bzoj discuss: http://www.lydsy.com/JudgeOnline/wttl/thread.php?tid=4493
标签:kd-tree read ttl open height alt png 复杂度 网上
原文地址:http://www.cnblogs.com/GXZlegend/p/7112932.html