标签:ges alt 有趣 ima 初学 分类器 分享 错误 贝叶斯分类器
今天稍微学了一下概率论,这里简单总结一下贝叶斯公式
因为是初学,所以整理的东西可能有错误orz
一、贝叶斯公式
其实就是由全概率公式推出来的
贝叶斯公式实际上是求出一个事件C的后验概率
首先给出样本空间A的若干个划分Bi,最后发生了结果C
那么可以得到下图
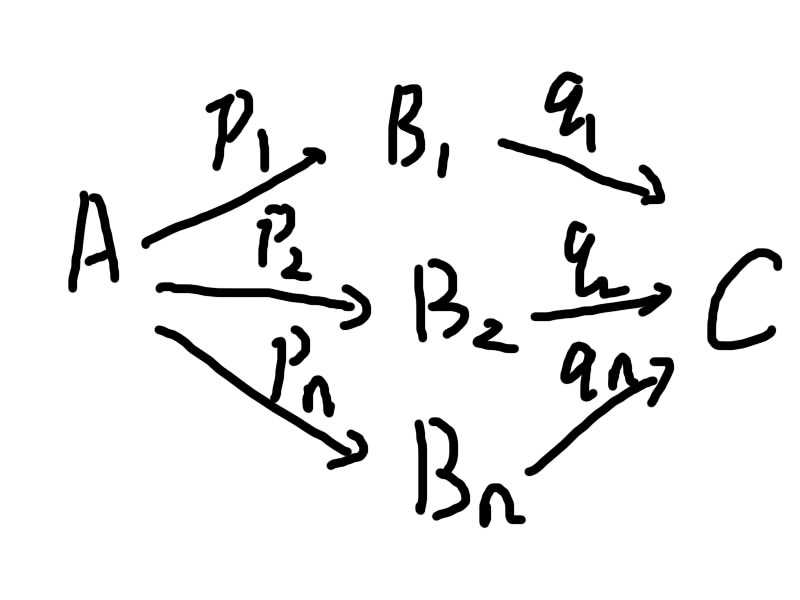
那么先验概率实际上就是p(B),后验概率是p(B|C)
下面给出公式
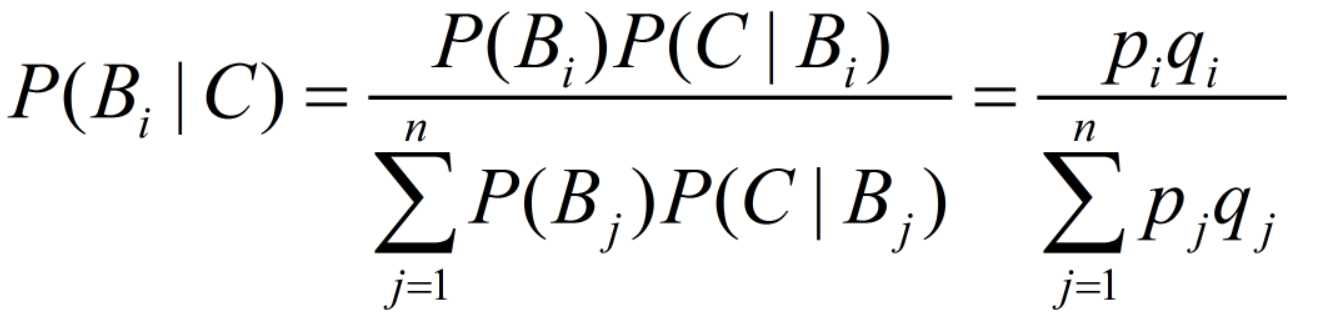
简单理解就是,如果结果C发生的话,条件是Bi的概率是多大。
而贝叶斯方法就是找到到底是哪个因素的概率最大
二、应用
实际上应用有很多,比如说贝叶斯网络和贝叶斯分类器都是基于贝叶斯方法的
这里分享一个有趣的问题, 蒙特霍尔问题,即三门问题
题目大意:
主持人给你三扇门,2个门里有羊,1个门里有车,你选定一个门但不打开
然后主持人选出另一个有羊的门打开,这时给你一个选择
你可以选择开你已经选择的门,或者换另一个门开
问哪种选择得到车的概率会更大。
这个题目,凭直觉想就是换不换门都是一样的,所以不需要换门
但是实际上换门的概率会更大,这里用贝叶斯方法简单证明
设Bi为第i扇门里有车的情况
那么样本空间就可以分成B1, B2, B3,它们的先验概率都是1/3
我们默认选1号门,因为选哪一个门都是一样的
而主持人选择3号门打开,记这个事件为C
我们来计算一下,此时的条件概率
P(C|B1) = 1/2
P(C|B2) = 1
P(C|B3) = 0
然后利用贝叶斯公式就可以算出P(B1|C) = 1/3, P(B2|C) = 2/3
也就是说换门的概率是不换门的2倍
另外P(B1|C)仍然是1/3,也就是说主持人的开门并不影响你选定门有车的概率(他们是独立的)
反而会影响另外那些门的概率
其实我们可以变成多门问题,就更直观了
如果有1000扇门,你先选定一门,主持人帮你排除一门
那么直观地想,选定的那一门显然概率是不变的,剩下的门因为排除的影响,所以概率会有所提高
同理这种思路也可以利用在三门问题里
标签:ges alt 有趣 ima 初学 分类器 分享 错误 贝叶斯分类器
原文地址:http://www.cnblogs.com/Saurus/p/7113502.html