标签:比较 == 人工 函数 ase 积累 hang ref 深度
读书期间对于深度学习也有涉及,不过只是皮毛,在这个数据和算法的时代,也需要更加贴近算法。于是从一名工程师角度出发,希望通过几篇文章,将深度学习基础记录下来,同时也是对于自己学习的总结和积累。总体思路是ANN-CNN-DNN,中间想起来有什么忘记的,也会加番。
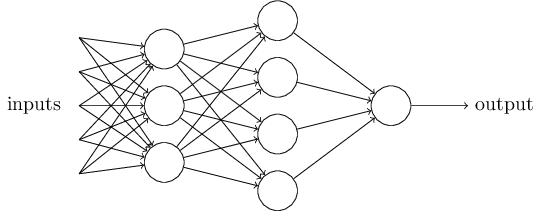
这是一张典型的人工神经网络的图,图中的节点称为神经元,图共分为三层,第一层为输入层,第二层为隐藏层,第三层为输出层。输入层接受外部世界的输入,具像化为图像的像素值,实体的特征值等,输出层概率预测结果,具像化为该图像是人像,该实体为潜在商家。
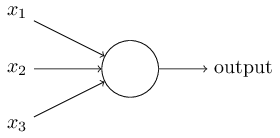
一个神经元将多个输入及其权值统一为下层节点的一个输入。例如: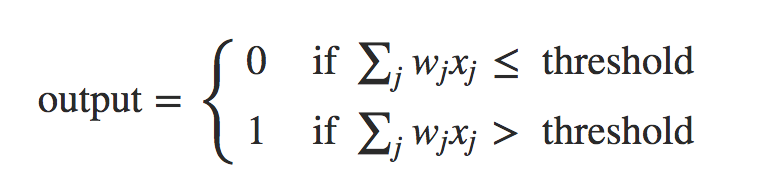
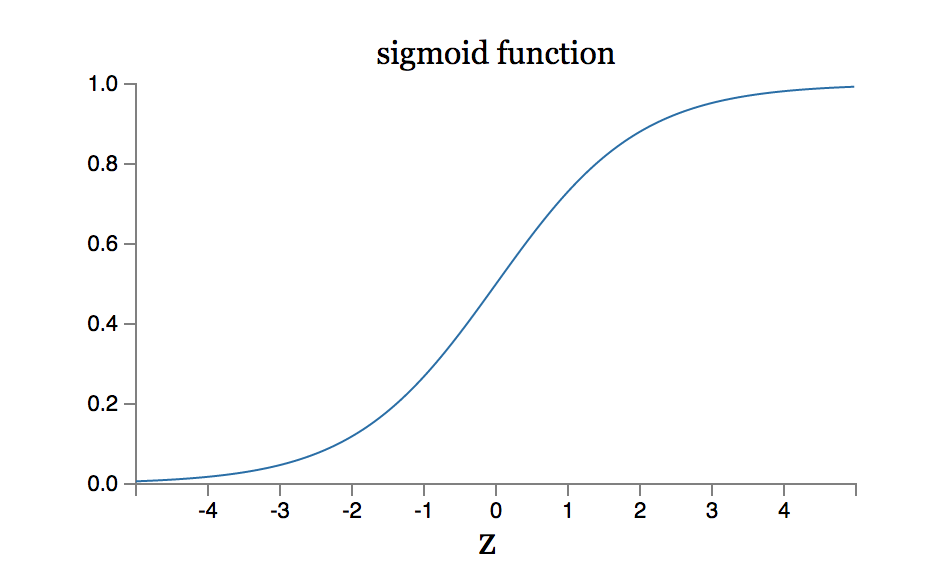
而神经元一般都使用sigmoid函数,至于为什么使用sigmoid函数,也是个很有探讨意义的问题,具体可以看这篇文章了解sigmoid的特性,http://www.tuicool.com/articles/uMraAb。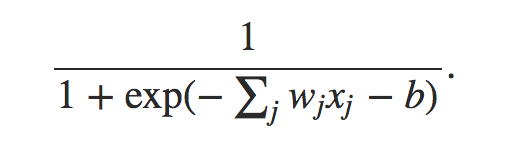
其中,w表示权重向量,x表示输入向量,b为该节点的阈值。
那么下面问题就是如何选择合适的权重和阈值,构建出来合适的网络。
网络结构往往决定了算法复杂度和模型可调度,输出层主要由向量决定,输出层主要由预测类型决定,主要问题就在中间层数和节点数的选择上,节点数和层数越多意味着模型可调节性越强,预测结果的粒度越细,但同时也意味着计算复杂度越高。经验中间层一般选1-2层,节点数作为可调参数。
首先,定义损失函数,损失函数的意义在于对于训练集评价预测结果和真实结果之间的差异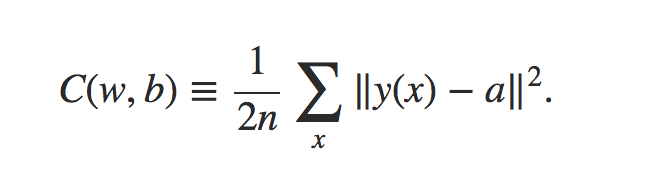
该损失函数其实是预测结果与真实结果之间的方差
我们希望通过调整权重w和阈值b的值来使预测结果和真实结果之间的差更小。相当于在一个解空间中寻找最优解。解法有很多,如梯度下降法,拟牛顿法等。
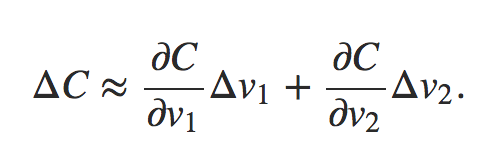
通过上述公式可以看出,对于损失函数的变化可以描述为损失在每个维度v上的变化值之和,用向量表示为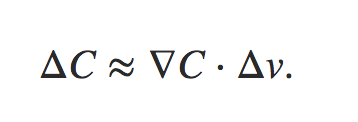
为了是损失更小而不是更大,损失的变化应该小于0,于是取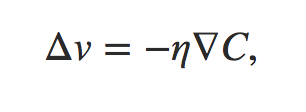
则,损失的下降可以表示为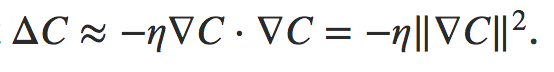
反向传播其实是对于当一次预测结束后,评估每个参数对于预测结果误差的贡献,并对其进行调整,调整方法可以通过损失函数对于权值的求导得到: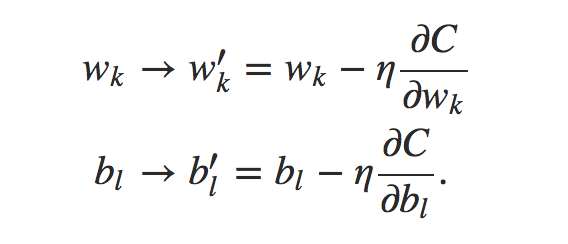
通过多次迭代,获得损失函数的极小值。步长决定了函数的收敛速度。
小结下:
人工神经网络就好像一个在陌生的城市迷路的孩子,每走一步都对该步进行评估,计算其到达目的地的可能性,并逐渐走到目的地。人工神经网络比较重要的有三部分:
-1. 结构:层级网络
-2. 求解方法:梯度下降
-3. 求解思想:反向传播
下集:一名工程师对于深度学习的理解-卷积神经网络CNN
标签:比较 == 人工 函数 ase 积累 hang ref 深度
原文地址:http://www.cnblogs.com/Gamay/p/7121192.html