标签:accept turn cst comm img alt file data cep
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 630 Accepted Submission(s): 232
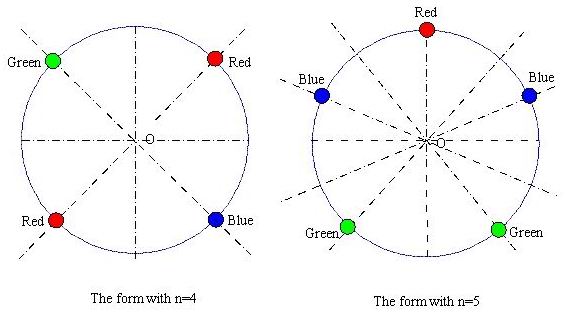
这道题和POJ2409是一样的题目,只不过这道题规定了颜色数目。
Polya定理的应用。先来看Polya定理。
Polya定理:设 G = {a1,a2,…,ag}是 N 个对象的置换群,用 M 种颜色给这 N 个对象着色,则不同的着色 方案数为:
|G|^(-1) * {M^c(a1) + M^c(a2) + … + M^c(ag)}。
其中 c(ai)为置换 ai 的循环节数,( i = 1,2,…,g )。
对于这道题,直接用Polya定理求解,找出所有的置换,并求出置换的循环节数。然后根据上边公式求出 3^c(ai) 的总和,再除以置换群个数。
题中有两种置换方式:
1.旋转置换。分别顺时针旋转 i 个珠子,其循环节长度为 LCM(N,i) / i,循环节数为
N / (LCM(N,i) / i),即 GCD(N,i)。
2.翻转置换。根据 N 的奇偶性分情况讨论。
N为奇数时:
以第 i 个珠子为顶点和中心翻转,翻转后,第 i 个珠子保持不变,其余珠子两两相互对换,因为有 N 个珠子,所以有 N 种翻转置换,每种翻转循环节数为 (N+1) / 2。
N为偶数时,有两种翻转方式:
以两边相对的两个珠子为轴和中心翻转,翻转后,这两个珠子保持不变,其余珠子两两相互对换,共有 N/2 种翻转置换,每种翻转循环节数为 (N+2) / 2。
以相邻的珠子中间连线为轴和中心翻转,翻转后,所有珠子两两相互对换,共有 N/2种翻转置换,每种翻转循环节数为 N/2。
注: 用long long 或__int64定义,本题的n可能是0,所以刚开始错误是RE,要特殊判断。
#include <iostream> #include<cstdio> #include<cstring> #include<cmath> using namespace std; long long res,n; long long gcd(long long a,long long b) { return b?gcd(b,a%b):a; } long long poww(long long a,long long b) { long long ans=1; while(b) { if (b%2==1) ans*=a; a*=a; b/=2; } return ans; } int main() { while(~scanf("%lld",&n)) { if (n==-1) break; if(n<=0) {printf("0\n"); continue;} res=0; for(long long i=1;i<=n;i++) res+=poww((long long)3,gcd(n,i)); if(n%2==1) res+=poww((long long)3,(n+1)/2)*n; else { res+=poww((long long)3,n/2+1)*(n/2); res+=poww((long long)3,n/2)*(n/2); } printf("%lld\n",res/(2*n)); } return 0; }
转自:http://blog.csdn.net/lianai911/article/details/48271557
hdu 1817 Necklace of Beads(Polya定理)
标签:accept turn cst comm img alt file data cep
原文地址:http://www.cnblogs.com/stepping/p/7121837.html