标签:state 类型 参数 noip ret 就会 make 存在 noi
Kiana最近沉迷于一款神奇的游戏无法自拔。
简单来说,这款游戏是在一个平面上进行的。
有一架弹弓位于(0,0)处,每次Kiana可以用它向第一象限发射一只红色的小鸟,小鸟们的飞行轨迹均为形如的曲线,其中a,b是Kiana指定的参数,且必须满足a<0。
当小鸟落回地面(即x轴)时,它就会瞬间消失。
在游戏的某个关卡里,平面的第一象限中有n只绿色的小猪,其中第i只小猪所在的坐标为(xi,yi)。
如果某只小鸟的飞行轨迹经过了(xi,yi),那么第i只小猪就会被消灭掉,同时小鸟将会沿着原先的轨迹继续飞行;
如果一只小鸟的飞行轨迹没有经过(xi,yi),那么这只小鸟飞行的全过程就不会对第i只小猪产生任何影响。
例如,若两只小猪分别位于(1,3)和(3,3),Kiana可以选择发射一只飞行轨迹为的小鸟,这样两只小猪就会被这只小鸟一起消灭。
而这个游戏的目的,就是通过发射小鸟消灭所有的小猪。
这款神奇游戏的每个关卡对Kiana来说都很难,所以Kiana还输入了一些神秘的指令,使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。
假设这款游戏一共有T个关卡,现在Kiana想知道,对于每一个关卡,至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算,所以希望由你告诉她。
输入格式:
第一行包含一个正整数T,表示游戏的关卡总数。
下面依次输入这T个关卡的信息。每个关卡第一行包含两个非负整数n,m,分别表示该关卡中的小猪数量和Kiana输入的神秘指令类型。接下来的n行中,第i行包含两个正实数(xi,yi),表示第i只小猪坐标为(xi,yi)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。
如果m=0,表示Kiana输入了一个没有任何作用的指令。
如果m=1,则这个关卡将会满足:至多用只小鸟即可消灭所有小猪。
如果m=2,则这个关卡将会满足:一定存在一种最优解,其中有一只小鸟消灭了至少只小猪。
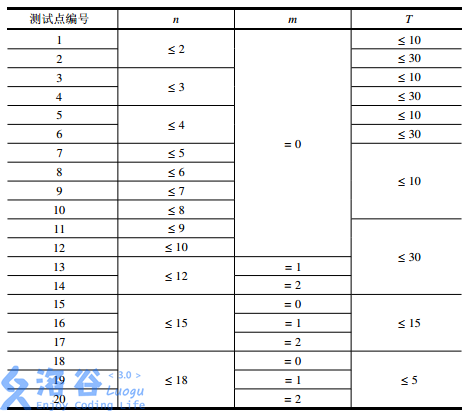
保证1<=n<=18,0<=m<=2,0<xi,yi<10,输入中的实数均保留到小数点后两位。
上文中,符号和
分别表示对c向上取整和向下取整
输出格式:
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数,表示相应的关卡中,消灭所有小猪最少需要的小鸟数量
2 2 0 1.00 3.00 3.00 3.00 5 2 1.00 5.00 2.00 8.00 3.00 9.00 4.00 8.00 5.00 5.00
1 1
3 2 0 1.41 2.00 1.73 3.00 3 0 1.11 1.41 2.34 1.79 2.98 1.49 5 0 2.72 2.72 2.72 3.14 3.14 2.72 3.14 3.14 5.00 5.00
2 2 3
1 10 0 7.16 6.28 2.02 0.38 8.33 7.78 7.68 2.09 7.46 7.86 5.77 7.44 8.24 6.72 4.42 5.11 5.42 7.79 8.15 4.99
6
【样例解释1】
这组数据中一共有两个关卡。
第一个关卡与【问题描述】中的情形相同,2只小猪分别位于(1.00,3.00)和 (3.00,3.00),只需发射一只飞行轨迹为y = -x^2 + 4x的小鸟即可消灭它们。
第二个关卡中有5只小猪,但经过观察我们可以发现它们的坐标都在抛物线 y = -x^2 + 6x上,故Kiana只需要发射一只小鸟即可消灭所有小猪。
【数据范围】
每次打出一条抛物线至少打下一头猪,要求最少次数,可以考虑宽搜+剪枝。每次发射的抛物线要么经过两头猪,这两头猪确定的这条抛物线上的所有猪都被打下;要么只经过一头猪,因为一点确定无数条抛物线,必定有一条只经过这一头猪,我们不关心这条抛物线具体是哪一条。
两点确定一条过原点的抛物线y=ax2+bx:点(x1, y1) (x2, y2)过抛物线,得y1=ax12+bx1,y2=ax22+bx2,两式分别变形得y1/x1-ax1=y2/x2-ax2=b,再整理得a=(y2/x2-y1/x1)/(x2-x1)。求出a后往回代可求出b。
由于猪最多只有18头,考虑状压,用一个32位数值型记录当前状态下被打掉的猪。则初始状态为(0)2,终止状态为(111...111)2。再预处理每两头猪确定的抛物线可以打下哪些猪。
题目给的m应该是用来xjb剪枝用的,但是m=2怎么用我也不懂……
注意事项:
浮点数判断相等,eps要取到1e-6,之前取1e-3被卡两个点。
剪枝用visited数组保存某个状态是否进过队,所以要在进队的时候赋值,之前乱搞成出队的时候赋值结果一片tle。
stl的queue不开优化会很慢,可以考虑手写队列。
1 #include <algorithm> 2 #include <cstring> 3 #include <iostream> 4 #include <queue> 5 #include <vector> 6 #include <cmath> 7 using namespace std; 8 bool equal(double x, double y, double eps = 0.000001) 9 { 10 return fabs(x - y) <= eps; 11 } 12 typedef pair<double, double> pig; 13 int n, m; 14 unsigned achievement; 15 pig pigs[20]; 16 unsigned pwxs[20][20]; 17 bool visited[(1 << 20)]; 18 int bfs() 19 { 20 typedef pair<unsigned, int> state; 21 queue<state> q; 22 q.push(make_pair(0, 0)); 23 while (!q.empty()) 24 { 25 state x = q.front(); 26 q.pop(); 27 if (x.first == achievement) 28 return x.second; 29 if (m == 1 && x.second > (int)(n * 1.0 / 3 + 3)) 30 continue; 31 for (int i = 1; i <= n; i++) 32 { 33 if (!(x.first & (1 << i))) 34 { 35 state y = x; 36 y.first |= (1 << i); 37 y.second++; 38 if (!visited[y.first]) 39 { 40 q.push(y); 41 visited[y.first] = true; 42 } 43 } 44 } 45 for (int i = 1; i <= n; i++) 46 { 47 for (int j = i + 1; j <= n; j++) 48 { 49 if (!(x.first & (1 << i)) && !(x.first & (1 << j))) 50 { 51 state y = x; 52 y.first |= pwxs[i][j]; 53 y.second++; 54 if (!visited[y.first]) 55 { 56 q.push(y); 57 visited[y.first] = true; 58 } 59 } 60 } 61 } 62 } 63 return -1; 64 } 65 int main() 66 { 67 ios::sync_with_stdio(false); 68 int t; 69 cin >> t; 70 while (t--) 71 { 72 memset(visited, false, 1 << 20); 73 cin >> n >> m; 74 for (int i = 1; i <= n; i++) 75 for (int j = 1; j <= n; j++) 76 pwxs[i][j] = 0; 77 achievement = 0; 78 for (int i = 1; i <= n; i++) 79 achievement |= (1 << i); 80 double a, b; 81 for (int i = 1; i <= n; i++) 82 { 83 cin >> a >> b; 84 pigs[i] = make_pair(a, b); 85 } 86 for (int i = 1; i <= n; i++) 87 { 88 for (int j = i + 1; j <= n; j++) 89 { 90 // y=ax^2+bx 91 // y1=ax1^2+bx1 92 // y2=ax2^2+bx2 93 // b=y1/x1-ax1 94 // =y2/x2-ax2 95 // a=(y2/x2-y1/x1)/(x2-x1) 96 double &x1 = pigs[i].first, &y1 = pigs[i].second; 97 double &x2 = pigs[j].first, &y2 = pigs[j].second; 98 double a = (y2 / x2 - y1 / x1) / (x2 - x1); 99 double b = y1 / x1 - a * x1; 100 if (a < 0) 101 { 102 for (int k = 1; k <= n; k++) 103 { 104 double &x = pigs[k].first, &y = pigs[k].second; 105 if (equal(a * x * x + b * x, y)) 106 pwxs[i][j] |= (1 << k); 107 } 108 } 109 } 110 } 111 cout << bfs() << endl; 112 } 113 return 0; 114 }
标签:state 类型 参数 noip ret 就会 make 存在 noi
原文地址:http://www.cnblogs.com/ssttkkl/p/7124206.html