标签:property min 森林 span alt minimum 没有 ima 生成
--------------------siwuxie095
最小生成树问题
这里介绍最小生成树(Minimum Spanning Tree)问题
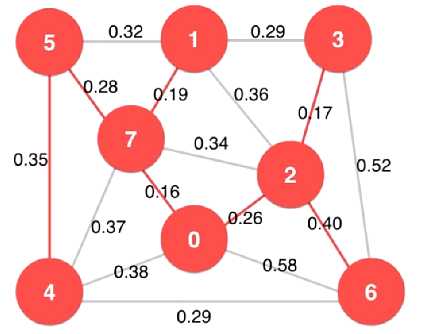
所谓生成树,就是对于一个完全连通的带权无向图,用 V-1 条边连接
V 个顶点而形成的树,即为该图的生成树,如上图所示
而在所有的生成树中,边上的权值相加最小的生成树,即为最小生成树,
如何找到一张图中的最小生成树,就是最小生成树问题
「最小生成树是一副连通加权无向图中一棵权值最小的生成树」
最小生成树问题,在实际生活中有很多应用,如:电缆的布线设计
通过发电站将电输送到每一个节点,其实并不需要每两个节点之间
都有电缆连接,只需要保证每个节点都有电即可。这种情况下,电
缆布线的最优设计就是找到这张图的最小生成树,让布置电缆的总
费用最低
即 最小生成树提供了一个各个节点之间均连通,同时连通的总费用
又最小的方案
对于最小生成树问题,通常针对的是连通带权无向图,所以最小生
成树必须要带权,不然就没有最小的概念了
如果一个图不连通,也可以分别在每个连通分量上求各自的最小生
成树,最后得到的通常叫做 最小生成森林
将最小生成树问题抽象出来,即 在有 V 个顶点的连通带权无向图
中找V-1 条边,这 V-1 条边必须将 V 个顶点连接起来,且使得最
终的总权值最小
1)找 V-1 条边
2)连接 V 个顶点
3)总权值最小
切分定理
实现最小生成树的 Prim 算法和 Kruskal 算法都不约而同的应用了
切分定理(Cut Property)
在介绍切分定理之前,首先应该知道什么叫做切分。把图中的顶点
分为两部分,称为这张图的一个切分(Cut)
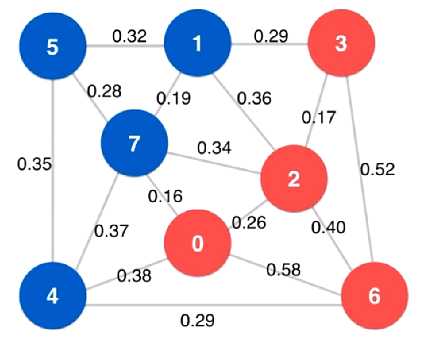
当定义了一个图的切分之后,就可以得到一个新的概念:
如果一条边的两个端点,属于切分不同的两个阵营,就称
这条边为横切边(Crossing Edge)
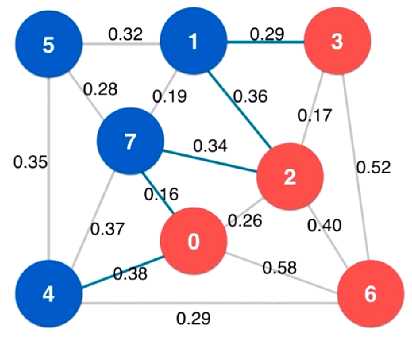
切分定理:
给定任意切分,横切边中权值最小的边必然属于最小生成树
如:在下图的切分中,横切边 0-7 是权值最小的边,权值为
0.16,所以 0-7 一定是这张图的最小生成树中的一条边
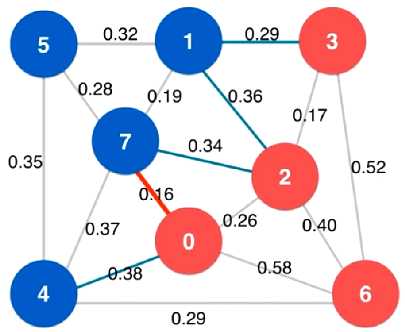
切分定理的简单证明:
前提:切分将一个图分成了两部分,中间用横切边进行连接。
根据切分定理可知,横切边中权值最小的边,一定属于最小
生成树
反证法:
令三条横切边分别为 e、f、g,且 e 为权值最小的横切边,
T 为图的最小生成树
假设 T 包含 f,而不包含 e,那么如果将 e 加入 T,那么
e 和 f 就必然形成了环,不再是生成树
显然,e 的权值小于 f,那么用 e 替换 f 就可以形成一个
权值小于 T 的生成树,与 T 为最小生成树矛盾
【made by siwuxie095】
标签:property min 森林 span alt minimum 没有 ima 生成
原文地址:http://www.cnblogs.com/siwuxie095/p/7124296.html