标签:16px 欧拉公式 最小 alt 最短时间 http 去掉 欧拉 技术
因为某种无法抗拒的原因,今天没有打比赛,所以也就没有那种心态。今天的题目有状压DP和二分,这套题不难也不简单,适中,适合我这种渣渣来做。在改题时,发现了许多问题。我连欧拉函数的计算都记错了,二分也忘记了。也总结出了一些经验,例如,在二分小数时,一定要比题目要求多加两位小数,这样也就避免了许多因为浮点数而造成的错误。长话短说,先看题。
T1 原根(math)
题目大意
给出两个定义,对于不超过m的正整数a,Gcd(m,a)=1,定义Ordm(a)为ad≡1(mod m)的最小正整数解。给出m,问有多少个a满足Ordm(a)=φ(m)
想法
这是一道数学题,当然就要想一些数学的方法来优化了
根据欧拉公式,若Gcd(a,m)=1,那么aφ(m)≡1(mod m),显然春天不远了d是不会大于φ(m)的。
然后,我们就按照题目说的做,喜欢的人可以加上快速幂优化。
其中,φ(m)是读phi,是有计算公式的!可以百度一下,你就会知道了
T2 道路覆盖(cover)
题目大意
ar把一段凹凸不平的路分成了高度不同的N段,并用H[i]表示第i段高度。现在Tar一共有n种泥土可用,它们都能覆盖给定的连续的k个部分。对于第i种泥土,它的价格为C[i],可以使得区间[i,min(n,i+k-1)] 的路段的高度增加E[i]。Tar要设定一种泥土使用计划,使得使用若干泥土后,这条路最低的高度尽量高,并且这个计划必须满足以下两点要求:
(1)每种泥土只能使用一次。
(2)泥土使用成本必须小于等于M。
请求出这个最低的高度最高是多少
想法
从“最低的高度最高”就可以看出,这道题是用二分的,正解就是二分答案。
从而,我们就把这道题目变为一道判定性的问题,给出一个mid,问你是否符合上面的题意。
普通方法使用递归判断可行性
既然可以用递归,那么显然可以用动态规划。
我们设F[i,s]表示你当前想选第i种泥土,前面k种的状态(包括i)是什么,用二进制表示。
我们用当前F[i,s]去更新F[i+1,s1]
关键是我们怎么转移。
对于每一种泥土,只有选和不选两种状态,那么我们只要考虑这两种情况就可以了
在此之前,我们先看一个东西
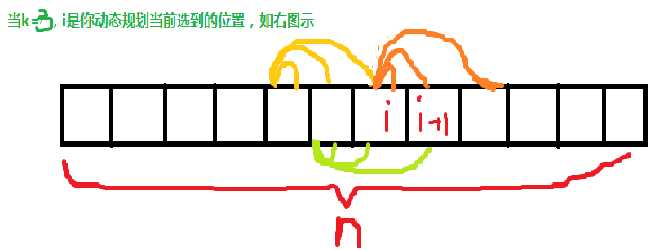
注意,我们这里是用i,更新i+1
读图可以发现,对i+1有影响的只有从i前k-1个(包括i)
可以发现,只有i包括i的前k-1个对i+1是有影响的。
因为你选到i时,状态是s,那么,如果从i更新到i+1,状态就是s去掉最后一位,也就是(s<<1),其实就是s/2
我们统计s状态中,有哪个地方是选了泥土的,然后记录一下,他们一共会让i+1这个位置的土地高多少,设这个数为num
①不选
如果不选,那么num+h[i]必定是大于mid的,这样才符合题目要求,如果不懂反复读上面的那句话,看看我画出来精美的图,就知道了。不懂都会懂
满足的上面的情况,我们就可以转移了
f[i,s<<1]:=min(f[i,s<<1],f[i,s])
②选
如果选,就要满足num+h[i]+E[i]是大于mid的
那么当前的位置s状态中i+1的位置应该是1,所以,我们就是要更新新的s
f[i,s<<1 or 1 shl (k-1)]:=min(f[i,s<<1 or 1 shl (k-1)],f[i,j]+c[i]);
这道题充分的体现了动态规划的屌
T3 迷宫花园(maze)
题目大意
知道左右走花费1时间,上下走花费v时间,v是未知的,给出一个图(有障碍),再给出从起点到终点最少花费的时间,求v的值。
想法
显然也是用二分,二分v的值
然后用得出来的v去跑一次SPFA或者DIS,看看最短时间是否为题目给定的。
这里总结出一点:
要是对于小数二分,一定要多二分几位。
有的人只要跑一次bfs,我觉得很神奇,但是也弄不清原因。
标签:16px 欧拉公式 最小 alt 最短时间 http 去掉 欧拉 技术
原文地址:http://www.cnblogs.com/2016fyj/p/7133068.html