标签:算法与数据结构 分治法 const lib 9.png blog ref load 表格
一、心得
递推方程式想清楚
二、题目及分析
问题描述:
设有n=2^k个运动员要进行网球循环赛。现要设计一个满足以下要求的比赛日程表:
(1)每个选手必须与其他n-1个选手各赛一次;
(2)每个选手一天只能参赛一次;
(3)循环赛在n-1天内结束。
请按此要求将比赛日程表设计成有n行和n-1列的一个表。在表中的第i行,第j列处填入第i个选手在第j天所遇到的选手。其中1≤i≤n,1≤j≤n-1。8个选手的比赛日程表如下图:

算法思路:按分治策略,我们可以将所有的选手分为两半,则n个选手的比赛日程表可以通过n/2个选手的比赛日程表来决定。递归地用这种一分为二的策略对选手进行划分,直到只剩下两个选手时,比赛日程表的制定就变得很简单。这时只要让这两个选手进行比赛就可以了。如上图,所列出的正方形表是8个选手的比赛日程表。其中左上角与左下角的两小块分别为选手1至选手4和选手5至选手8前3天的比赛日程。据此,将左上角小块中的所有数字按其相对位置抄到右下角,又将左下角小块中的所有数字按其相对位置抄到右上角,这样我们就分别安排好了选手1至选手4和选手5至选手8在后4天的比赛日程。依此思想容易将这个比赛日程表推广到具有任意多个选手的情形。
算法步骤:
(1)用一个for循环输出日程表的第一行 for(int i=1;i<=N;i++) a[1][i] = i

(2)然后定义一个m值,m初始化为1,m用来控制每一次填充表格时i(i表示行)和j(j表示列)的起始填充位置。
(3)用一个for循环将问题分成几部分,对于k=3,n=8,将问题分成3大部分,第一部分为,根据已经填充的第一行,填写第二行,第二部分为,根据已经填充好的第一部分,填写第三四行,第三部分为,根据已经填充好的前四行,填写最后四行。for (ints=1;s<=k;s++) N/=2;
(4)用一个for循环对③中提到的每一部分进行划分for(intt=1;t<=N;t++)对于第一部分,将其划分为四个小的单元,即对第二行进行如下划分

同理,对第二部分(即三四行),划分为两部分,第三部分同理。
(5)最后,根据以上for循环对整体的划分和分治法的思想,进行每一个单元格的填充。填充原则是:对角线填充
for(int i=m+1;i<=2*m;i++) //i控制行
for(int j=m+1;j<=2*m;j++) //j控制列
{
a[i][j+(t-1)*m*2]= a[i-m][j+(t-1)*m*2-m];/*右下角的值等于左上角的值 */
a[i][j+(t-1)*m*2-m] =a[i-m][j+(t-1)*m*2];/*左下角的值等于右上角的值 */
}
运行过程:
(1)由初始化的第一行填充第二行

(2)由s控制的第一部分填完。然后是s++,进行第二部分的填充

(3)最后是第三部分的填充

三、代码及结果
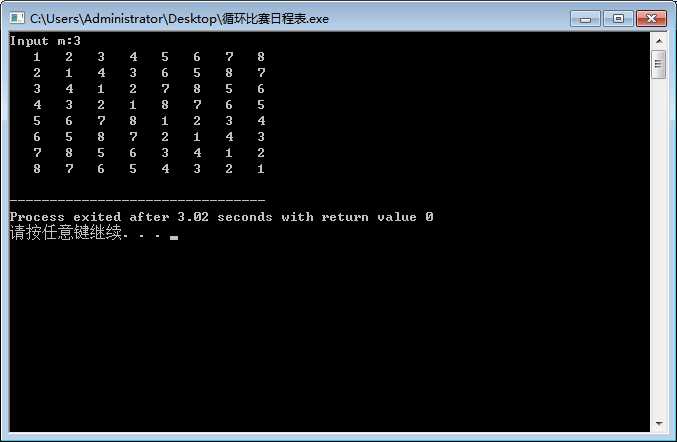
1 //递推方程式想清楚 2 #include <iostream> 3 using namespace std; 4 5 const int MAXN=1025,MAXM=11; 6 int marchlist[MAXN][MAXN]; 7 int m; 8 9 int main(){ 10 printf("Input m:"); 11 scanf("%d",&m); 12 int n=1<<m,k=1,half=1; 13 marchlist[0][0]=1; 14 while(k<=m){ 15 for(int i=0;i<half;i++){ 16 for(int j=0;j<half;j++){ 17 marchlist[i][j+half]=marchlist[i][j]+half; 18 } 19 } 20 for(int i=0;i<half;i++){ 21 for(int j=0;j<half;j++){ 22 marchlist[i+half][j]=marchlist[i][j+half]; 23 marchlist[i+half][j+half]=marchlist[i][j]; 24 } 25 } 26 half*=2; 27 k++; 28 } 29 for(int i=0;i<n;i++){ 30 for(int j=0;j<n;j++){ 31 printf("%4d",marchlist[i][j]); 32 } 33 printf("\n"); 34 } 35 return 0; 36 } 37
标签:算法与数据结构 分治法 const lib 9.png blog ref load 表格
原文地址:http://www.cnblogs.com/Renyi-Fan/p/7138773.html