标签:二叉树 结构 建立 节点 函数 turn http 递归 img
线段树是一种二叉搜索树。
它将一个区间划分成一些子区间,每个子区间对应线段树中的一个叶节点。
对于线段树中的每一个非叶子节点[a,b],它的左儿子表示的区间为[a,(a+b)>>1],右儿子表示的区间为[(a+b)>>1+1,b]。也就是说线段树是一棵平衡二叉树。
下图是对于[1,10]的区间构造的一棵线段树。
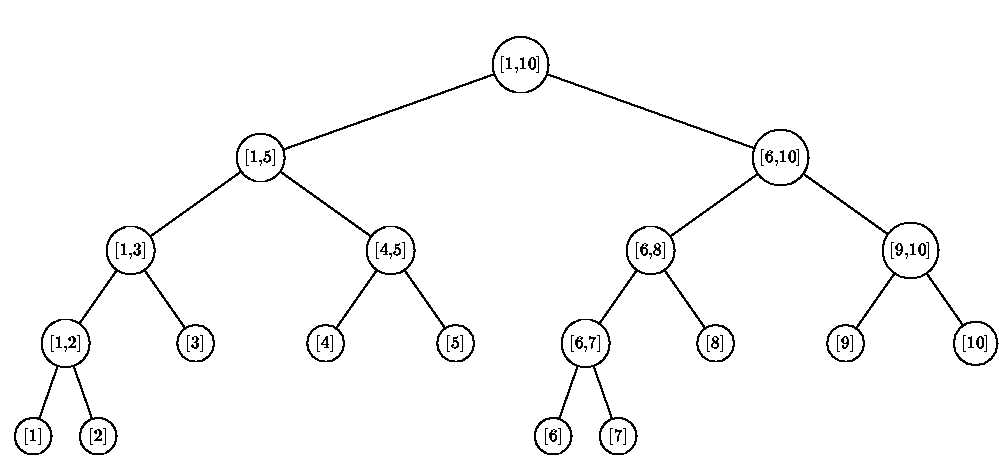
线段树的基本操作函数有三个。
分别是build(建树),update(更新),query(查询区间和)。
线段树定义:
struct node{ int left,right; //左子树和右子树 int sum; //节点区间和 }tree[MAX_N];
线段树建树:
void build(int l,int r,int num) { tree[num].left=l; tree[num].right=r; if(l==r) return; //叶子节点 int mid=(l+r)>>1; //二分建树 build(l,mid,num<<1); //递归建立左子树 build(mid+1,r,num<<1|1); //递归建立右子树 }
线段树更新:
void update(int l,int r,int value,int num) { //叶子节点 if(tree[num].left==tree[num].right) return; int mid=(tree[num].left+tree[num].right)>>1; //如果所要更新的点的右端小于mid或左端点大于mid,则直接更新l到r的值 if(r<=mid) update(l,r,value,num<<1); else if(l>mid) update(l,r,value,num<<1|1); //如果要更新的点在mid两边,则两边分别更新 else{ update(l,mid,value,num<<1); update(mid+1,r,value,num<<1|1); } }
线段树查询:
int query(int l,int r,int num) { //叶子节点 if(l==tree[num].left && r==tree[num].right) return tree[num].sum; int mid=(tree[num].left+tree[num].right)>>1; //和更新类似 if(r<=mid) return query(l,r,num<<1); if(l>mid) return query(l,r,num<<1|1); else return query(l,mid,num<<1)+query(mid+1,r,num<<1|1); }
线段树应用:连续区间动态查询,连续区间统计等。
时间复杂度:基本保证每个操作为O(logN)。
标签:二叉树 结构 建立 节点 函数 turn http 递归 img
原文地址:http://www.cnblogs.com/YSFAC/p/7141841.html