标签:line unsigned max sqrt ifd 证明 ++i getc style
传送门:http://acm.hdu.edu.cn/showproblem.php?pid=5828
【题解】
考虑bzoj3211 花神游历各国,只是多了区间加操作。
考虑上题写法,区间全为1打标记。考虑推广到这题:如果一个区间max开根和min开根相同,区间覆盖标记。
巧的是,这样复杂度是错的!
e.g:
$n = 10^5, m = 10^5$
$a[] = \{1, 2, 1, 2, ... , 1, 2\}$
$operation = \{ "1~1~n~2", "2~1~n", "1~1~n~2", "2~1~n", ... \}$
然后发现没有可以合并的,每次都要暴力做,复杂度就错了。
考虑对于区间的$max-min \leq 1$的情况维护:
当$max=min$,显然直接做即可。
当$max=min+1$,如果$\sqrt{max} = \sqrt{min}$,那么变成区间覆盖;否则$\sqrt{max} = \sqrt{min} + 1$,变成区间加法。
都是线段树基本操作,所以可以做。
下面证明复杂度为什么是对的:
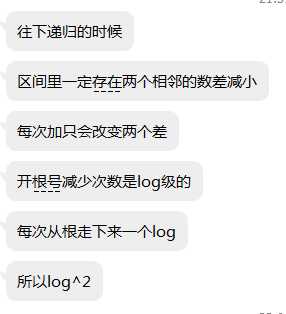
时间复杂度$O(nlog^2n)$。

# include <math.h> # include <stdio.h> # include <string.h> # include <iostream> # include <algorithm> // # include <bits/stdc++.h> # ifdef WIN32 # define LLFORMAT "%I64d" # else # define LLFORMAT "%lld" # endif using namespace std; typedef long long ll; typedef long double ld; typedef unsigned long long ull; const int N = 1e5 + 10; const int mod = 1e9+7; inline int getint() { int x = 0; char ch = getchar(); while(!isdigit(ch)) ch = getchar(); while(isdigit(ch)) x = (x<<3) + (x<<1) + ch - ‘0‘, ch = getchar(); return x; } int n, a[N]; const int SN = 262144 + 5; struct SMT { ll mx[SN], mi[SN], s[SN], tag[SN], cov[SN]; # define ls (x<<1) # define rs (x<<1|1) inline void up(int x) { mx[x] = max(mx[ls], mx[rs]); mi[x] = min(mi[ls], mi[rs]); s[x] = s[ls] + s[rs]; } inline void pushtag(int x, int l, int r, ll tg) { mx[x] += tg, mi[x] += tg; s[x] += tg * (r-l+1); tag[x] += tg; } inline void pushcov(int x, int l, int r, ll cv) { mx[x] = cv, mi[x] = cv; s[x] = cv * (r-l+1); cov[x] = cv; tag[x] = 0; } inline void down(int x, int l, int r) { register int mid = l+r>>1; if(cov[x]) { pushcov(ls, l, mid, cov[x]); pushcov(rs, mid+1, r, cov[x]); cov[x] = 0; } if(tag[x]) { pushtag(ls, l, mid, tag[x]); pushtag(rs, mid+1, r, tag[x]); tag[x] = 0; } } inline void build(int x, int l, int r) { tag[x] = cov[x] = 0; if(l == r) { mx[x] = mi[x] = s[x] = a[l]; return ; } int mid = l+r>>1; build(ls, l, mid); build(rs, mid+1, r); up(x); } inline void edt(int x, int l, int r, int L, int R, int d) { if(L <= l && r <= R) { pushtag(x, l, r, d); return ; } down(x, l, r); int mid = l+r>>1; if(L <= mid) edt(ls, l, mid, L, R, d); if(R > mid) edt(rs, mid+1, r, L, R, d); up(x); } inline void doit(int x, int l, int r) { if(mx[x] == mi[x]) { register ll t = mx[x]; pushtag(x, l, r, ll(sqrt(t)) - t); return ; } if(mx[x] == mi[x] + 1) { register ll pmx = ll(sqrt(mx[x])), pmi = ll(sqrt(mi[x])); if(pmx == pmi) pushcov(x, l, r, pmx); else pushtag(x, l, r, pmx - mx[x]); // mx[x] = mi[x] + 1 return ; } down(x, l, r); int mid = l+r>>1; doit(ls, l, mid); doit(rs, mid+1, r); up(x); } inline void edt(int x, int l, int r, int L, int R) { if(L <= l && r <= R) { doit(x, l, r); return ; } down(x, l, r); int mid = l+r>>1; if(L <= mid) edt(ls, l, mid, L, R); if(R > mid) edt(rs, mid+1, r, L, R); up(x); } inline ll sum(int x, int l, int r, int L, int R) { if(L <= l && r <= R) return s[x]; down(x, l, r); int mid = l+r>>1; ll ret = 0; if(L <= mid) ret += sum(ls, l, mid, L, R); if(R > mid) ret += sum(rs, mid+1, r, L, R); return ret; } }T; inline void sol() { n = getint(); register int Q = getint(), op, l, r, x; for (int i=1; i<=n; ++i) a[i] = getint(); T.build(1, 1, n); while(Q--) { op = getint(), l = getint(), r = getint(); if(op == 1) { x = getint(); T.edt(1, 1, n, l, r, x); } else if(op == 2) T.edt(1, 1, n, l, r); else printf(LLFORMAT "\n", T.sum(1, 1, n, l, r)); } } int main() { int T = getint(); while(T--) sol(); return 0; }
标签:line unsigned max sqrt ifd 证明 ++i getc style
原文地址:http://www.cnblogs.com/galaxies/p/hdu5828.html