标签:clu n+1 char ima using 部分 正方形 ++ getc
很久以前,有一个强大的帝国,它的国土成正方形状,如图所示。
这个国家有若干诸侯。由于这些诸侯都曾立下赫赫战功,国王准备给他们每人一块封地(正方形中的一格)。但是,这些诸侯又非常好战,当两个诸侯位于同一行或同一列时,他们就会开战。如下图2—3为n=3时的国土,阴影部分表示诸侯所处的位置。前两幅图中的诸侯可以互相攻击,第三幅则不可以。
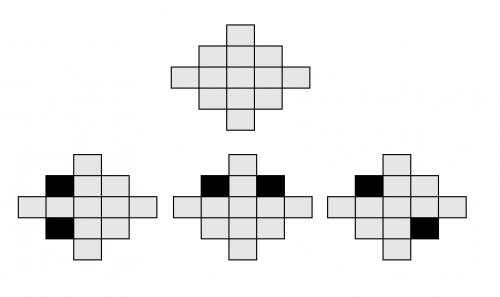
国王自然不愿意看到他的诸侯们互相开战,致使国家动荡不安。 因此,他希望通过合理的安排诸侯所处的位置,使他们两两之间都不能攻击。
现在,给出正方形的边长n,以及需要封地的诸侯数量k,要求你求出所有可能的安置方案数。(n≤l00,k≤2n2-2n+1)
由于方案数可能很多,你只需要输出方案数除以504的余数即可。
输入格式:
仅一行,两个整数n和k,中间用一空格隔开。
输出格式:
一个整数,表示方案数除以504的余数。
2 2
4
注意:镜面和旋转的情况属于不同的方案。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=1000+5; const int mod=504; int f[maxn][maxn],num[maxn]; int n,m,ans; int read() { int x=0,f=1; char ch=getchar(); while(ch>‘9‘||ch<‘0‘) {if(ch==‘-‘) f=-1; ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘; ch=getchar();} return x*f; } int main() { n=read();m=read(); num[1]=num[2]=1; for(int i=3;i<=2*n-1;i++) num[i]=num[i-2]+2; f[0][0]=1; for(int i=1;i<=2*n-1;i++) for(int j=1;j<=i;j++) for(int k=j-1;k<=i-1;k++) f[i][j]+=f[k][j-1]*(num[i]-j+1),f[i][j]%=mod; for(int i=m;i<=2*n-1;i++) ans+=f[i][m],ans%=mod; printf("%d",ans); return 0; }
标签:clu n+1 char ima using 部分 正方形 ++ getc
原文地址:http://www.cnblogs.com/huihao/p/7172394.html