标签：i++ example http number str int 构建 for pair
Fibonotci sequence is an integer recursive sequence defined by the recurrence relation
Sequence s is an infinite and almost cyclic sequence with a cycle of length N. A sequence s is called almost cyclic with a cycle of length N if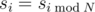 
, for i?≥?N, except for a finite number of values si, for which 
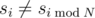(i?≥?N).
Following is an example of an almost cyclic sequence with a cycle of length 4:
Notice that the only value of s for which the equality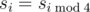 
does not hold is s6 (s6?=?7 and s2?=?8). You are given s0,?s1,?...sN?-?1 and all the values of sequence s for which 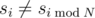(i?≥?N).
Find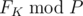 
.
The first line contains two numbers K and P. The second line contains a single number N. The third line contains N numbers separated by spaces, that represent the first N numbers of the sequence s. The fourth line contains a single number M, the number of values of sequence s for which 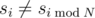. Each of the following M lines contains two numbers j and v, indicating that 
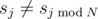and sj?=?v. All j-s are distinct.
Output should contain a single integer equal to .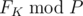
10 8
3
1 2 1
2
7 3
5 4
4
感觉是递推神题……f[n]=s[n-1]*f[n-1]+s[n-2]*f[n-2]，而且{s[i]}是个T=5w的循环数列，而且还换掉了s[i]当中5w个点……
先不考虑几个s[i]的特殊点
都算到f[1e18]了肯定是要用到矩阵快速幂了
构建矩阵比较简单：
f[n] f[n-1] * s[n] 1 = f[n+1] f[n]
0 0 s[n-1] 0 0 0
那么
f[1] f[0] * s[1] 1 * s[2] 1 * ..... * s[n-1] 1 = f[n] f[n-1]
0 0 s[0] 0 s[1] 0 s[n-2] 0 0 0
然后注意到s[i]是个循环的
所以就是算出一个循环内的转移矩阵的乘积，一个循环是
s[1] 1 ~ s[T] 1
s[0] 0 s[T-1] 0
接下来直接快速幂即可。
然后考虑挖点的情况：对于一个s[k]的修改，实际上有两个矩阵受到了它的影响：
s[k] 1 和 s[k+1] 1
s[k-1] 0 s[k] 0
所以每个修改拆成2个对矩阵里头的值的修改。这样就是对矩阵的单点修改不超过10w个
所有s[k]的修改按照k排个序
然后维护一个线段树，保存一个周期内的矩阵的乘积（对你没看错，线段树存的是矩阵）
每次同一个周期内的修改就直接在线段树上单点修改，做完之后ans乘个当前1到T的区间积，然后再单点改回去，下个周期再改。这样每个修改就是logT的
改回去的时候搞个栈就好了
最后输出个答案矩阵的左上角
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdlib> 5 #include<algorithm> 6 #include<cmath> 7 #include<queue> 8 #include<deque> 9 #include<set> 10 #include<map> 11 #include<ctime> 12 #define LL long long 13 #define inf 0x7ffffff 14 #define pa pair<int,int> 15 #define mkp(a,b) make_pair(a,b) 16 #define pi 3.1415926535897932384626433832795028841971 17 using namespace std; 18 inline LL read() 19 { 20 LL x=0,f=1;char ch=getchar(); 21 while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} 22 while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} 23 return x*f; 24 } 25 LL k,mod,T,C,cnt; 26 LL s[100010]; 27 struct matrix{ 28 LL a[2][2]; 29 inline void init(){a[0][0]=a[0][1]=a[1][0]=a[1][1]=0;} 30 matrix operator *(matrix b) 31 { 32 matrix ans;ans.init(); 33 for (int k=0;k<=1;k++) 34 for (int i=0;i<=1;i++) 35 for (int j=0;j<=1;j++) 36 ans.a[i][j]=(ans.a[i][j]+a[i][k]*b.a[k][j])%mod; 37 return ans; 38 } 39 }ans; 40 inline matrix getm(LL x) 41 { 42 matrix c; 43 c.a[0][0]=s[x];c.a[0][1]=1;c.a[1][0]=s[x-1];c.a[1][1]=0; 44 return c; 45 } 46 struct segtree{ 47 int l,r; 48 matrix m; 49 }t[800010]; 50 int zhan[1000010],top; 51 inline void update(int k){t[k].m=t[k<<1].m*t[k<<1|1].m;} 52 inline void buildtree(int now,int l,int r) 53 { 54 t[now].l=l;t[now].r=r; 55 if (l==r) 56 { 57 t[now].m=getm(l); 58 return; 59 } 60 int mid=(l+r)>>1; 61 buildtree(now<<1,l,mid); 62 buildtree(now<<1|1,mid+1,r); 63 update(now); 64 } 65 inline void change(int now,int x,matrix m) 66 { 67 int l=t[now].l,r=t[now].r; 68 if (l==r){t[now].m=m;return;} 69 int mid=(l+r)>>1; 70 if (x<=mid)change(now<<1,x,m); 71 else change(now<<1|1,x,m); 72 update(now); 73 } 74 inline matrix ask(int now,int x,int y) 75 { 76 int l=t[now].l,r=t[now].r; 77 if (l==x&&r==y)return t[now].m; 78 int mid=(l+r)>>1; 79 if (y<=mid)return ask(now<<1,x,y); 80 else if (x>mid)return ask(now<<1|1,x,y); 81 else return ask(now<<1,x,mid)*ask(now<<1|1,mid+1,y); 82 } 83 inline matrix quickpow(matrix a,LL b) 84 { 85 matrix s;s.init();s.a[0][0]=s.a[1][1]=1; 86 while (b) 87 { 88 if (b&1)s=s*a; 89 a=a*a; 90 b>>=1; 91 } 92 return s; 93 } 94 struct cg{LL pos,rnk,x,op;}c[100010],lst; 95 bool operator <(cg a,cg b){return a.rnk<b.rnk||a.rnk==b.rnk&&a.pos<b.pos;} 96 bool operator <=(cg a,cg b){return !(b<a);} 97 int main() 98 { 99 k=read();mod=read();T=read(); 100 if (k==0){puts("0");return 0;} 101 if (k==1){printf("%d\n",1%mod);return 0;} 102 k--;lst.rnk=k/T+(k%T!=0);lst.pos=k%T;if (!lst.pos)lst.pos=T; 103 for (int i=0;i<T;i++)s[i]=read();s[T]=s[0]; 104 C=read(); 105 for (int i=1;i<=C;i++) 106 { 107 LL a=read(),b=read(); 108 c[++cnt].rnk=a/T+(a%T!=0); 109 c[cnt].pos=a%T;if (!c[cnt].pos)c[cnt].pos=T; 110 c[cnt].x=b;c[cnt].op=1; 111 112 c[++cnt].rnk=a/T+1; 113 c[cnt].pos=a%T+1; 114 c[cnt].x=b;c[cnt].op=2; 115 } 116 sort(c+1,c+cnt+1); 117 buildtree(1,1,T); 118 ans.a[0][0]=1; 119 LL now2=0; 120 for (int i=1;i<=cnt;i++) 121 { 122 if(c[i]<=lst) 123 { 124 if (c[i].rnk-1!=now2) 125 { 126 ans=ans*ask(1,1,T); 127 while (top){change(1,zhan[top],getm(zhan[top]));top--;} 128 now2++; 129 if(now2!=c[i].rnk-1)ans=ans*quickpow(ask(1,1,T),c[i].rnk-1-now2),now2=c[i].rnk-1; 130 } 131 matrix chg=ask(1,c[i].pos,c[i].pos); 132 if (c[i].op==1)chg.a[0][0]=c[i].x;else chg.a[1][0]=c[i].x; 133 change(1,c[i].pos,chg); 134 zhan[++top]=c[i].pos; 135 }else 136 { 137 if (now2<lst.rnk-1) 138 { 139 ans=ans*ask(1,1,T); 140 while (top){change(1,zhan[top],getm(zhan[top]));top--;} 141 now2++; 142 if (now2<lst.rnk-1)ans=ans*quickpow(ask(1,1,T),lst.rnk-1-now2); 143 } 144 ans=ans*ask(1,1,lst.pos); 145 printf("%lld\n",ans.a[0][0]);return 0; 146 } 147 } 148 if (now2<lst.rnk-1) 149 { 150 ans=ans*ask(1,1,T); 151 while (top){change(1,zhan[top],getm(zhan[top]));top--;} 152 now2++; 153 if (now2<lst.rnk-1)ans=ans*quickpow(ask(1,1,T),lst.rnk-1-now2); 154 } 155 ans=ans*ask(1,1,lst.pos); 156 printf("%lld\n",ans.a[0][0]);return 0; 157 }
标签：i++ example http number str int 构建 for pair
原文地址：http://www.cnblogs.com/zhber/p/7172952.html
