CX老湿经常被人黑,被黑得多了,自己也就麻木了。于是经常听到有人黑他,他都会深情地说一句:禽兽啊!
一天CX老湿突发奇想,给大家出了一个难题,并且声称谁能够准确地回答出问题才能继续黑他,否则他就要反击了。
这个难题就是:
给出两个数p和q,接下来q个询问,每个询问给出两个数A和B,请分别求出:
一、有多少个有序数对(x,y)满足1<=x<=A,1<=y<=B,并且gcd(x,y)为p的一个约数;
二、有多少个有序数对(x,y)满足1<=x<=A,1<=y<=B,并且gcd(x,y)为p的一个倍数。
只有一组测试数据。
第一行两个数:p和q。(1<p<10^7 ,1<q<1000。)
接下来有q行,每行两个数A和B。(1<A,B<10^7)
输出共q行。每行两个数。用空格隔开。
分别表示题目描述中的两个对应的答案。
(x,y)=(2,3)和(x,y)=(3,2)被视为两个不同有序数对哦!
对于64位整型请用lld,或者cin,cout。T_T
CSU_LQ
这一道题是去年的一次比赛的题,当时觉得用欧拉能做,然后很难实现。
后来知道用莫比乌斯反演来做,但是一直超时。已经使用分块了,还是超时。
题意:略
思路:对于第二种,直接(A/p)*(B/p)就是答案。不难理解。
对于第一种情况:
设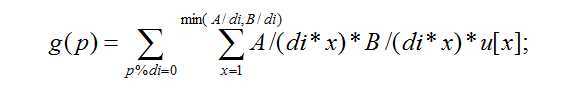
g(p)代表枚举P的每一因子 di 求gcd(x,y)=di (1<=x<=A,1<=y<=B)的累加和。
就是题意要求的值。
如果此时,枚举每一个P的因子di 来求,就会超时。
这个式子可以转化一下,另T = di*x,那么式子可以转化为:
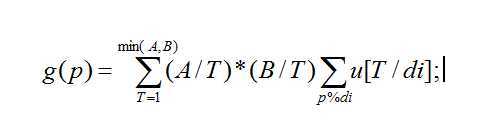
这样的话,我们只需要先预处理后一部分,就可以用sqrt(min(A,B)) 的时间解决这个问题。
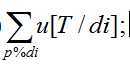 这部分如何预处理呢?
这部分如何预处理呢?
首先我们先打表求出u[];
分析这个式子,设tom(T) = sigma(u[di],T%di==0&&di是P的因子);
由于p是唯一的,我们求出它的因子,然后用它的因子筛选一下数组hxl[ ] ,就是tom(T);
最后hxl[],前n项和,用分块来做,完毕。
1 #include<iostream>
2 #include<stdio.h>
3 #include<cstring>
4 #include<cstdlib>
5 #include<math.h>
6 using namespace std;
7
8 typedef long long LL;
9 const int maxn = 1e7+1;
10 bool s[maxn];
11 int prime[670000],len = 0;
12 int yz[10002],ylen;
13 int mu[maxn];
14 int hxl[maxn];
15 void init()
16 {
17 memset(s,true,sizeof(s));
18 mu[1] = 1;
19 for(int i=2;i<maxn;i++)
20 {
21 if(s[i] == true)
22 {
23 prime[++len] = i;
24 mu[i] = -1;
25 }
26 for(int j=1;j<=len && ((long long)prime[j])*i<maxn;j++)
27 {
28 s[i*prime[j]] = false;
29 if(i%prime[j]!=0)
30 mu[i*prime[j]] = -mu[i];
31 else
32 {
33 mu[i*prime[j]] = 0;
34 break;
35 }
36 }
37 }
38 }
39 void solve(int p)
40 {
41 ylen = 0;
42 int k = (int)sqrt(p*1.0);
43 int tmp;
44 for(int i=1;i<=k;i++)
45 {
46 if(p%i==0)
47 {
48 yz[++ylen] = i;
49 tmp = p/i;
50 if(tmp!=i) yz[++ylen] = tmp;
51 }
52 }
53 for(int i=1;i<=ylen;i++)
54 {
55 for(int j=yz[i],k=1;j<maxn;j=j+yz[i],k++)
56 hxl[j]=hxl[j]+mu[k];
57 }
58 for(int i=2;i<maxn;i++) hxl[i] = hxl[i]+hxl[i-1];
59 }
60 int main()
61 {
62 init();
63 int p,q,A,B;
64 scanf("%d%d",&p,&q);
65 solve(p);
66 while(q--)
67 {
68 scanf("%d%d",&A,&B);
69 if(A>B) swap(A,B);
70 long long ans1 = 0,ans2 = 0;
71 for(int i=1,la = 0;i<=A; i=la+1)
72 {
73 la = min(A/(A/i),B/(B/i));
74 ans1 = ans1+(long long)(hxl[la]-hxl[i-1])*(A/i)*(B/i);
75 }
76 ans2 = (A/p)*(B/p);
77 printf("%lld %lld\n",ans1,ans2);
78 }
79 return 0;
80 }
81
82 /**************************************************************
83 Problem: 1325
84 User: 987690183
85 Language: C++
86 Result: Accepted
87 Time:1052 ms
88 Memory:92044 kb
89 ****************************************************************/

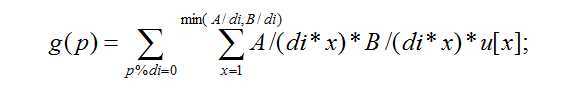
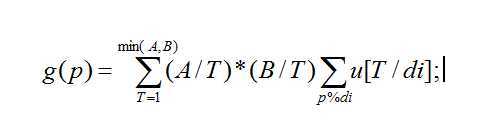
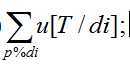 这部分如何预处理呢?
这部分如何预处理呢?