标签:image 方向 完成 依据 margin 镜像 size 而在 实现
1、天线阵形
应用在一维阵列的空间平滑算法,要求在天线阵所在的一维空间内,存在两个以上完全相同的子阵,子阵的数量决定阵列能够解决的相参(干)信号源的数目,阵列共能对子阵阵元数-1个信号进行测向。
相对于均匀阵列,非均匀阵具有较大的测向范围,较优的最大基线,且能够降低阵元间隔大于信号最小半波长所引起的谱峰模糊,因此本方案拟采取非均匀线阵作为目标子阵,并对三种低阵元数,包含两个对称子阵的阵列进行了仿真分析。
按空间平滑算法的排布要求,非均匀阵列仅可共用一个阵元,同时两子阵的距离远远大于信号的半波长,在多信号时,已受模糊影响产生较较多伪峰。为了降低工程的实现成本,提高阵元的复用率,同时尽可能的缩短两子阵的平滑距离,本方案采用了前后向平滑算法。不同的布阵方案中,对称子阵的共用阵元数为2~3个。
设阵元能实现的最小半径r=1.3cm,则本方案分析的3种阵列如下所示。
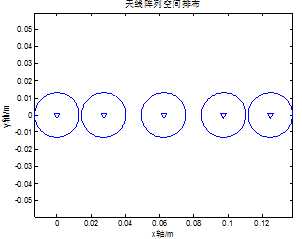
图1 共用3阵元的5元阵
图1中为共用2、3、4三个阵元的5元非均匀线阵在空间中的排布示例,其中第[1, 2, 3, 4]为第一个子阵,[2, 3, 4, 5]为第二个子阵,本方案的仿真间隔为[2.1, 2.7, 2.7, 2.1]r。
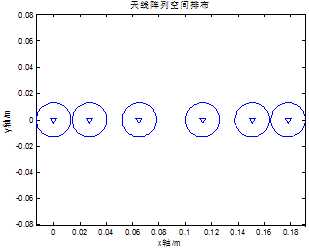
图2 共用2阵元的6元阵
图2中为共用3、4三个阵元的6元非均匀线阵在空间中的排布示例,其中第[1, 2, 3, 4]为第一个子阵,[3, 4, 5, 6]为第二个子阵,本方案的仿真间隔为[2.1, 2.9, 3.7, 2.9, 2.1]r。
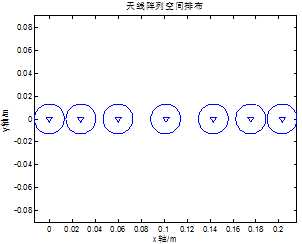
图3 共用3个阵元的7元均匀线阵
图3中为共用3、4、5三个阵元的/7元非均匀线阵在空间中的排布示例,其中第[1, 2, 3, 4, 5]为第一个子阵,[3, 4, 5, 6, 7]为第二个子阵,本方案的仿真间隔为[2.1,2.5, 3.2, 3.2, 2.5, 2.1]r。
前后向空间平滑算法是指将具有基准子阵对称结构的子阵,通过反相+反向,进行镜像翻转,从而获得与基准子阵形状一致阵列接收数据协方差矩阵的一种空间平滑算法。该算法能够较好地增加阵元的复用率,减少空间平滑算法所需的物理阵元数,降低工程的实现成本。
设具有对称结构子阵的接收数据矩阵为,基准子阵的数据矩阵为,则本方案的前后向空间平滑算法可表示为:
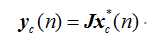
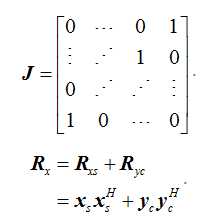
所得的数据协方差矩阵Rx再按MUSIC算法进行处理。
采用中心频率为18GHz,带宽10MHz,采样频率40MHz,采样点数16点,信噪比分别为10dB,9dB,0dB的线性调频信号进行仿真。
试验1:三种算法的解相干能力及算法的正确性
两信号中心频率相差1k,信噪比10dB信号入射方向为40°,信噪比9dB信号入射方向为45°。
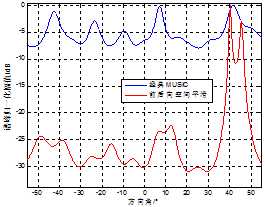
(a)5元阵
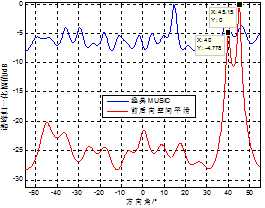
(b) 6元阵
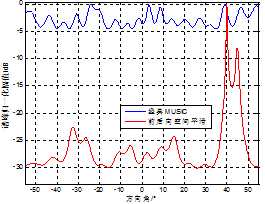
(c) 7元阵
图4 2相干信号入射空间谱
图中可以看出三红阵形都能较为准确的测出两个相干信号的来波方向,未经平滑处理的经典MUSIC算法基本失效,但是在信噪干比比较小时,通过谱峰大小区分信号与反射干扰不能保证完全正确,如图(b)。
试验2:3信号2相干信号入射
信噪比10dB信号入射方向为35°,信噪比9dB相干信号入射方向为40°,信噪比0dB独立信号入射方向为45°。
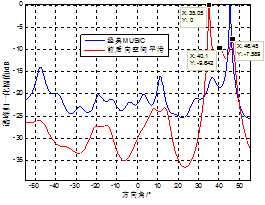
(a) 5元阵
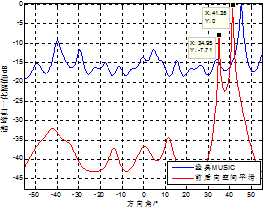
(b) 6元阵
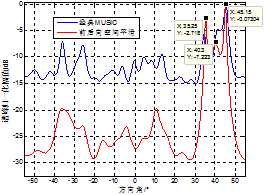
(c) 7元阵
图 5 3信号2相干入射空间谱
从图5 (a)、图5 (c)中可以看出,共用3阵元的两个非均匀阵列,其子阵的平滑距离相对较小,能够分辨出3个不同来波方向的信号,但因为共用3个阵元导致各阵元间隔比较接近,模糊产生的伪峰较高;而共用2阵元的6元阵只有两个较为尖锐的谱峰,且受到低信噪比独立信号的影响,40°处的来波方向估计值产生了较大误差。
试验3: 3个相干信号入射
信噪比为0dB信号也为相干干扰信号,其他条件与试验2相同。
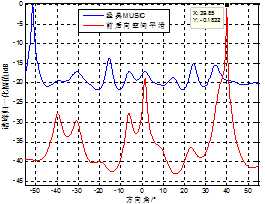
(a) 5元阵
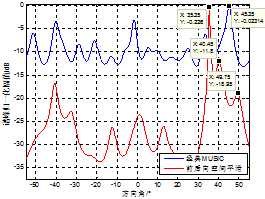
(b) 6元阵

(c) 7元阵
图6 3相干信号入射空间谱
依据空间平滑算法的原理,具有两个子阵的天线平滑算法无法完成3个相干信号的测向,而在实际环境中,可能存在其他较为微弱的相参(干)反射干扰,该干扰会对算法的测向结果产生较大影响。图6 (a)与图6 (c)中可以看出,5元阵与7元阵已经完全分辨不出相干信号谱峰,而共用两阵元的6元阵,其复用的信息较少,受低信噪比相干信号的影响较小,依然能够较为准确地测出两个相干信号的来波方向。
根据上述仿真结果可以看出前后向空间平滑算法能够较好地估计出两个相参(干)信号的来波方向,阵元复用率的提高,会导致小信号对算法误差的影响增大。根据实际的应用环境,可以选择增加子阵数量,或增加子阵阵元数来降低其他信号对直射信号测向结果的影响。
标签:image 方向 完成 依据 margin 镜像 size 而在 实现
原文地址:http://www.cnblogs.com/xingshansi/p/7173086.html