标签:src while scanf bsp 模板 logs des width ios
定义:f0=f1=1, fn=fn-1+fn-2(n>=2)。{fi}称为Fibonacci数列。
输入n,求fn mod q。其中1<=q<=30000。
第一行一个数T(1<=T<=10000)。
以下T行,每行两个数,n,q(n<=109, 1<=q<=30000)
文件包含T行,每行对应一个答案。
3
6 2
7 3
7 11
1
0
10
1<=T<=10000
n<=109, 1<=q<=30000
感谢:这道题卡了一天,最后发现自己是被坑了,我一直以为斐波那契数列f0=0,f1=f2=1,结果这是f0=f1=1;
好吧这只是我智障了,我还是来说说矩阵怎么做吧
首先矩阵乘法的定义:
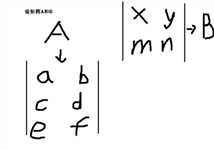
A和B两个矩阵乘出来是
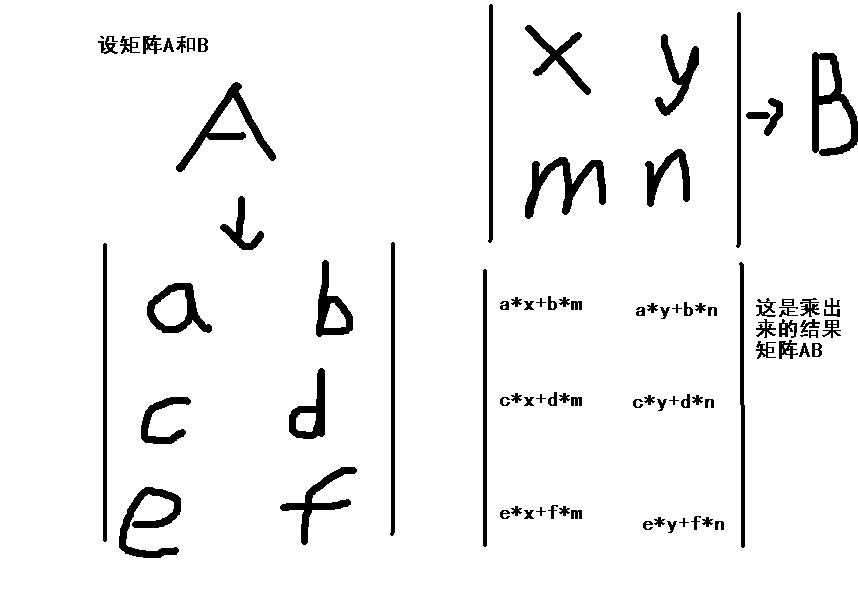
知道矩阵是怎么样乘后就可以来解决这道题,我们定义一个初始矩阵和单位矩阵
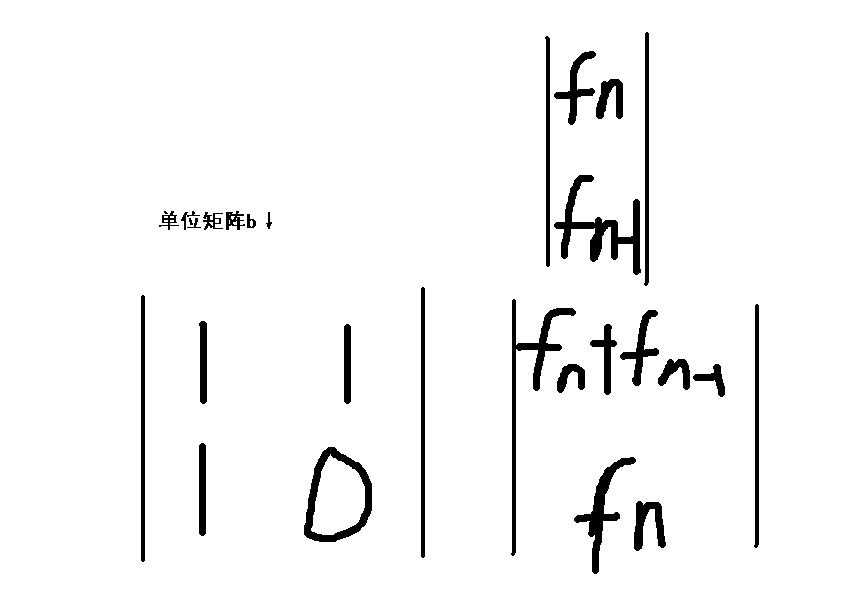
而fn+fn-1=fn+1,所以这就是这道题的关键了
例如我要求f6 就要用初识矩阵*b^5,而初识矩阵ans[1][1]=f1=1,ans[1][2]=f0=1
当数据比较大的时候这个b^n-1次方可能就会爆,所以这又要用到快速幂
然后我们来看个快速幂模板
//求a^b %c void done(int a,int b,int c) {
ans=1; while(b) { if(b&1) ans=(ans*a)%c; a=(a*a)%c; b>>=1; } }
有了这两个知识,我们就可以实现矩阵快速幂了
代码如下:
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<iostream> 5 using namespace std; 6 7 long long ans[3][2],c[5][5],b[5][5]; 8 long long n,m,t; 9 10 void dod(int n) 11 { 12 while(n) 13 { 14 if(n&1)//判断n的奇偶性 15 { 16 for(int i=1;i<=2;i++) 17 for(int j=1;j<=1;j++) 18 { 19 for(int k=1;k<=2;k++) 20 c[i][j]=(c[i][j]+ans[k][j]*b[i][k])%m;//这个地方的i,j,k建议画图分析 21 } 22 for(int i=1;i<=2;i++) 23 for(int j=1;j<=1;j++) 24 { 25 ans[i][j]=c[i][j]; 26 c[i][j]=0; 27 } 28 } 29 for(int i=1;i<=2;i++) 30 for(int j=1;j<=2;j++) 31 { 32 for(int k=1;k<=2;k++) 33 c[i][j]=(c[i][j]+b[i][k]*b[k][j])%m; 34 } 35 for(int i=1;i<=2;i++) 36 for(int j=1;j<=2;j++) 37 { 38 b[i][j]=c[i][j]; 39 c[i][j]=0; 40 } 41 n>>=1; 42 43 } 44 45 } 46 47 int main() 48 { 49 cin>>t; 50 while(t--) 51 { 52 scanf("%lld%lld",&n,&m); 53 b[1][1]=b[1][2]=b[2][1]=1; 54 ans[1][1]=ans[2][1]=1; 55 b[2][2]=0; 56 n--;//fn只需要初识矩阵*b^n-1 57 dod(n); 58 printf("%lld\n",ans[1][1]%m); 59 } 60 61 }
讲题略水,如有错误,望诸位大佬指出
标签:src while scanf bsp 模板 logs des width ios
原文地址:http://www.cnblogs.com/Danzel-Aria233/p/7181859.html