标签:return 匈牙利 data 算法思想 没有 int 说明 最小 printf
补坑时间到QAQ
好吧今天讲的是网络流建模与二分图匹配。。。
day3的网络流建模好像说的差不多了、(囧)
那就接着补点吧。。
既然昨天讲了建图思想,那今天就讲讲网络流最重要的技巧:拆点。
拆点,顾名思义,就是把一个状态拆成数个点以满足题目要求。
今天主要围绕一个例题来讲:修车。(虽然是丧题,但是却是网络流算法思想实现的典例)
——————————————————我是分割线——————————————————
题目:
同一时刻有位车主带着他们的爱车来到了汽车维修中心。维修中心共有M位技术人员,不同的技术人员对不同的车进行维修所用的时间是不同的。现在需要安排这M位技术人员所维修的车及顺序,使得顾客平均等待的时间最小。 说明:顾客的等待时间是指从他把车送至维修中心到维修完毕所用的时间。注:(2<=m<=9,1<=n<=60)
——————————————————我是分割线——————————————————
其实我一开始看到这题,我都没看出来这是网络流(真是太弱了)
然后我去网络上看了题解。
首先我们知道一个工人修一辆车就会让其余没有修过车的time增加,所以我们发现如果考虑第i个工人修第j辆车的话,会发现时间是不确定的。
但是如果我们倒着过来计算的话,那么我们就能够计算时间了。
所以我们将n个工人每一个分为m个点,表示第i个工人修倒数第j辆车,然后每一条边的费用就是time*j,表示等待的时间,从S到每一个点连边,从每一个点到T连边,然后我们跑最小费用最大流就好了。
对于费用流不懂的同学们可以去我的博客上看看。(暂时没写,以后补坑)
下面附上例题代码
#include<algorithm> #include<cstdio> #include<cmath> #include<cstring> #include<iostream> int ans; int go[200005],tot,S,T,first[200005],next[200005],flow[200005]; int cost[200005],c[200005],edge[200005],from[200005],a[500][500]; int nodes,b[500][500],n,m,op[200005],dis[200005],vis[200005]; int read(){ int t=0,f=1;char ch=getchar(); while (ch<‘0‘||ch>‘9‘){if (ch==‘-‘) f=-1;ch=getchar();} while (‘0‘<=ch&&ch<=‘9‘){t=t*10+ch-‘0‘;ch=getchar();} return t*f; } void insert(int x,int y,int z,int l){ tot++; go[tot]=y; next[tot]=first[x]; first[x]=tot; flow[tot]=z; cost[tot]=l; } void add(int x,int y,int z,int l){ insert(x,y,z,l);op[tot]=tot+1; insert(y,x,0,-l);op[tot]=tot-1; } bool spfa(){ for (int i=0;i<=T;i++) dis[i]=0x3f3f3f3f,vis[i]=0; dis[S]=0; int h=1,t=1; c[1]=S; while (h<=t){ int now=c[h++]; for (int i=first[now];i;i=next[i]){ int pur=go[i]; if (flow[i]&&dis[pur]>dis[now]+cost[i]){ dis[pur]=dis[now]+cost[i]; from[pur]=now; edge[pur]=i; if (vis[pur]) continue; vis[pur]=1; c[++t]=pur; } } vis[now]=0; } return dis[T]!=0x3f3f3f3f; } void updata(){ int mn=0x7fffffff; for (int i=T;i!=S;i=from[i]){ mn=std::min(mn,flow[edge[i]]); } for (int i=T;i!=S;i=from[i]){ flow[edge[i]]-=mn; flow[op[edge[i]]]+=mn; ans+=mn*cost[edge[i]]; } } int main(){ m=read();n=read(); for (int i=1;i<=n;i++){ for (int j=1;j<=m;j++){ a[i][j]=read(); } } S=0,T=n*m+n+1; for (int i=1;i<=n;i++) add(S,i,1,0); nodes=n; for (int i=1;i<=m;i++) for (int k=1;k<=n;k++) b[i][k]=++nodes,add(nodes,T,1,0); for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) for (int k=1;k<=n;k++) add(i,b[j][k],1,k*a[i][j]); while (spfa()) updata(); double Ans=(double)ans/n; printf("%.2f\n",Ans); }
接下来我们讲讲二分图匹配。
二分图匹配就是说有一个二层图,层数不同的两个点之间有一些边,问如何选取一些边,使得一个点只被一条边选中,而且边的个数最多(求最大匹配)
其中最主要的算法就是匈牙利算法,朴素而迅速。
我们上图。
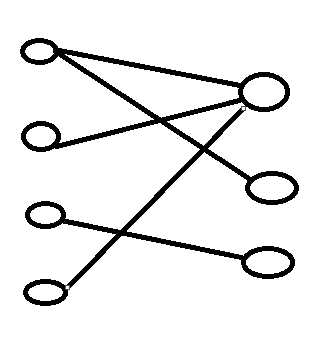
对于这个图我们先选到这一条边
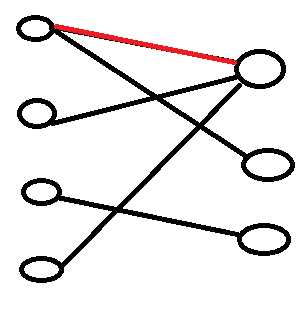
然后我们找到下一个点,发现它连接的一条边的终点已经被选中了,所以我们试着让第一个点重新匹配一个没有被匹配过的节点
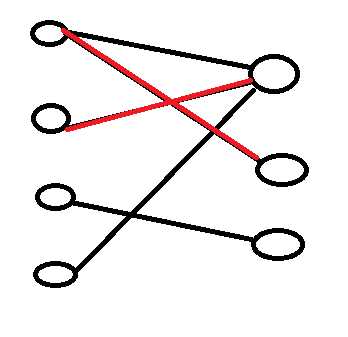
然后我们找到第三个节点,发现可以匹配。
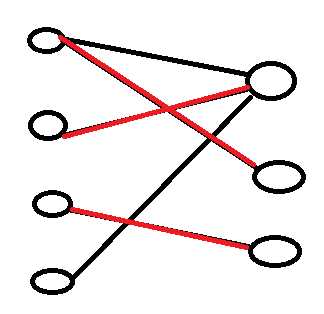
当我们找到第四个节点时,发现它所对应的节点没有办法修改匹配,至此匈牙利算法结束,最大匹配为3
而在我们进行匈牙利算法的时候有一些优化可以实现,比如如果一个点已经尝试匹配过,而且失败了,那么我们就不要尝试匹配了。(类似dfs减枝)
下面贴上算法
bool match(int u){ S[u]=1; for(int i=head[u];i;i=g[i].next) if(!T[g[i].to]){ T[g[i].to]=1; if(!lky[g[i].to]||match(lky[g[i].to])){ lky[g[i].to]=u;lkx[u]=g[i].to;return true; } } return false; }
注:现在起所有的算法如果我没有写例题我都只会列出核心代码,剩下的东西请视情况补充。QAQ
标签:return 匈牙利 data 算法思想 没有 int 说明 最小 printf
原文地址:http://www.cnblogs.com/ghostfly233/p/7168300.html