
标签:题解 ring out content include type can stream ret

输入文件的第一行输入两个正整数 。
如题
N,M<=10^15
题解:STEP 1:
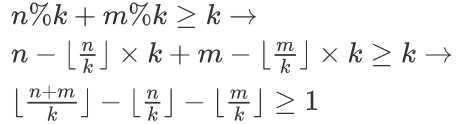
这步还是很容易的吧~毕竟原来的式子不太舒服。但是注意,最后一个式子的取值只能为0或1,所以就变成了。
![]()
STEP 2:
![]()
这步倒是难理解一些,但是考虑:我们将这三个等式都算出来,如果满足了左边那个条件,那么这三个等式加起来为1,对答案的贡献正好为$\varphi(k)$。否则,因为左边的式子不是0就是1,那么只能是0,这三个等式加起来对答案的贡献也就是0。
STEP 3:这三个式子长得差不多,我们只考虑一个
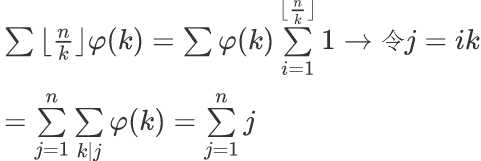
这步就显得比较套路了。我们强行给那个底式赋予实际意义,然后就转化成了简单的欧拉函数性质应用。三个式子都算完后,你发现结果正好是nm。那么最终的答案就是$\varphi(n)\varphi(m)nm$
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
typedef long long ll;
const ll mod=998244353;
typedef long long ll;
ll n,m;
ll phi(ll x)
{
ll ret=x,i;
for(i=2;i*i<=x;i++)
{
if(x%i==0)
{
ret=ret/i*(i-1);
while(x%i==0) x/=i;
}
}
if(x!=1) ret=ret/x*(x-1);
return ret%mod;
}
int main()
{
scanf("%lld%lld",&n,&m);
printf("%lld",phi(n)*phi(m)%mod*(n%mod)%mod*(m%mod)%mod);
return 0;
}
标签:题解 ring out content include type can stream ret
原文地址:http://www.cnblogs.com/CQzhangyu/p/7189732.html