标签:lock water color rect 经典的游戏 问题: ping logs 运动
【SinGuLaRiTy-1026】 Copyright (c) SinGuLaRiTy 2017. All Rights Reserved.
特工玛利亚被送到S市执行一个特别危险的任务。她需要利用地铁完成他的任务,S市的地铁只有一条线路运行,所以并不复杂。
玛利亚有一个任务,现在的时间为0,她要从第一个站出发,并在最后一站的间谍碰头。玛利亚知道有一个强大的组织正在追踪她,她知道如果一直呆在一个车站,她会有很大的被抓的风险,躲在运行的列车中是比较安全的。所以,她决定尽可能地呆在运行的列车中,她只能往前或往后坐车。
玛利亚为了能准时且安全的到达最后一个车站与对方碰头,需要知道在在车站最小等待时间总和的计划。你必须写一个程序,得到玛丽亚最短的等待时间。当然,到了终点站之后如果时间还没有到规定的时刻,她可以在车站里等着对方,只不过这个等待的时刻也是要算进去的。
这个城市有n个车站,编号是1-n,火车是这么移动的:从第一个车站开到最后一个车站。或者从最后一站发车然后开会来。火车在每特定两站之间行驶的时间是固定的,我们也可以忽略停车的时间,玛利亚的速度极快,所以他可以迅速上下车即使两辆车同时到站。
输入文件包含多组数据,每组数据都由7行组成
第1行:一个正整数N(2<=N<=50)表示站的数量
第2行:一个正整数T(0<=T<=200)表示需要的碰头时间
第3行:1-(n-1)个正整数(0<ti<70)表示两站之间列车的通过时间
第4行:一个整数M1(1<=M1<=50)表示离开第一个车站的火车的数量
第5行:M1个正整数:d1,d2……dn,(0<=d<=250且di<di+1)表示每一列火车离开第一站的时间
第6行:一个正整数M2(1<=M2<=50)表示离开第N站的火车的数量
第7行:M2个正整数:e1,e2……eM2,(0<=e<=250且ei<ei+1)表示每一列火车离开第N站的时间
最后一行有一个整数0。
对于每个测试案例,打印一行“Case Number N: ”(N从1开始)和一个整数表示总等待的最短时间或者一个单词“impossible”如果玛丽亚不可能做到。按照样例的输出格式。
| 样例输入 | 样例输出 |
|
4 |
Case Number 1: 5 |
一道DP题目,dp[i][j]表示到达第i个城市的时候 ,时间为j的等待时间最少是多少,然后转移方程即可。
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cmath>
#include<iostream>
#define MAXN 110
using namespace std;
int a[MAXN];
int d1[MAXN][MAXN],d2[MAXN][MAXN];
int m1,m2;
int dp[MAXN][400];
int main()
{
int n;
int T=1;
while(scanf("%d",&n)&&n!=0)
{
int t;
scanf("%d",&t);
for(int i=1;i<=n-1;i++)
scanf("%d",&a[i]);
scanf("%d",&m1);
for(int i=1;i<=m1;i++)
scanf("%d",&d1[1][i]);
sort(d1[1]+1,d1[1]+m1+1);
scanf("%d",&m2);
for(int i=1;i<=m2;i++)
scanf("%d",&d2[n][i]);
sort(d2[n]+1,d2[n]+m2+1);
dp[0][1]=0;
for(int i=1;i<=m1;i++)
for(int j=1;j<=n-1;j++)
d1[j+1][i]=d1[j][i]+a[j];
for(int i=1;i<=m2;i++)
for(int j=n-1;j>=1;j--)
d2[j][i]=d2[j+1][i]+a[j];
for(int i=0;i<=t;i++)
for(int j=1;j<=n;j++)
dp[j][i]=t+1;
dp[1][0]=0;
for(int j=0;j<=t;j++)
for(int i=1;i<=n;i++)
if(dp[i][j]<=t)
{
int k;
for(k=1;k<=m1;k++)
if(d1[i][k]>=j)
break;
if(d1[i][k]-j+dp[i][j]<dp[i+1][j+a[i]+d1[i][k]-j]&&k<=m1)
dp[i+1][j+a[i]+d1[i][k]-j]=d1[i][k]-j+dp[i][j];
for(k=1;k<=m2;k++)
if(d2[i][k]>=j)
break;
if(k<=m2&&d2[i][k]-j+dp[i][j]<dp[i-1][j+a[i-1]+d2[i][k]-j])
dp[i-1][j+a[i-1]+d2[i][k]-j]=d2[i][k]-j+dp[i][j];
}
for(int i=1;i<=t;i++)
if(dp[n][i]<t)
dp[n][t]=min(dp[n][i]+t-i,dp[n][t]);
if(dp[n][t]<=t)
printf("Case Number %d: %d\n",T++,dp[n][t]);
else
printf("Case Number %d: impossible\n",T++);
}
return 0;
}
或许你曾听过巴比伦塔的传说,现在这个故事的许多细节已经被遗忘了。现在,我们要告诉你整个故事:
巴比伦人有n种不同的积木,每种积木都是实心长方体,且数目都是无限的。第i种积木的长宽高分别为{xi,yi,zi}。积木可以被旋转,所以前面的长宽高是可以互换的。也就是其中2个组成底部的长方形,剩下的一个为高度。巴比伦人想要的用积木来尽可能地建更高的塔,但是两块积木要叠在一起是有条件的:只有积木A的底部2个边均小于积木B的底部相对的2个边时,这积木A才可以叠在积木B上方。例如:底部为3x8的积木可以放在底部为4x10的积木上,但是无法放在底部为6x7的积木上。
给你一些积木的数据,你的任务是写一个程式算出可以堆出的塔最高是多少。
输入数据会包含多组数据。
在每一组数据中:第1行包含一个整数n,表示有n (1<=n<=30)种不同的积木。接下来的n行,每行给出3个整数,表示一块积木的长宽高。
当n=0时,输入数据结束。
对于每一组数据,按照以下格式输出答案:
Case case: maximum height = height
| 样例输入 | 样例输出 |
|
1 |
Case 1: maximum height = 40 |
乍一看,有点像最长上升子序列类型的题目。对于积木可以翻转这一个条件,我们可以把不同状态(总共有6种,自己画图吧)下的积木看成不同种类的积木。为了方便以后DP的判断,我们在DP之前先小小地预处理以下:对每一种积木,按照底面积由小到大排序。后面的DP过程比较好想,大家可以看代码。
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#define MAXN 30*6+10
using namespace std;
struct Block
{
int x,y,h;
void fun(int a,int b,int c)
{
x=a;
y=b;
h=c;
}
}node[MAXN];
bool cmp(Block r,Block t)
{
return r.x*r.y<t.x*t.y;
}
int dp[MAXN];
int main()
{
int num,cnt=0;
while(scanf("%d",&num)!=EOF)
{
if(!num)
return 0;
int a,b,c;
int m=0;
for(int i=0;i<num;i++)
{
cin>>a>>b>>c;
node[m++].fun(a, b, c);
node[m++].fun(a, c, b);
node[m++].fun(b, a, c);
node[m++].fun(b, c, a);
node[m++].fun(c, a, b);
node[m++].fun(c, b, a);
}
sort(node,node+m,cmp);
int maxlen=0;
memset(dp,0,sizeof(dp));
for(int i=0;i<m;i++)
{
dp[i]=node[i].h;
for(int j=0;j<i;j++)
if(node[i].x>node[j].x&&node[i].y>node[j].y)
dp[i]=max(dp[i],dp[j]+node[i].h);
if(dp[i]>maxlen)
maxlen=dp[i];
}
cout<<"Case "<<++cnt<<": maximum height = "<<maxlen<<endl;
}
return 0;
}
John Doe是一名出色的飞行员。一次,他决定租一架小飞机开始旅行一些美丽的地方。John Doe为自己设计的飞行路线满足以下要求:
1>路线经过所有的城市;2>路线从最左边的地方开始,先严格向右,到达最右边的地方后,再严格向左回到出发的地方;3>两个地点之间的路线是直线。
现在,给出每一个点的坐标,请你求出满足要求的最短路线的长度。
一句话题意:有n个点,给出x、y坐标。找出一条路,从最左边的点出发,严格向右走到达最右点再严格向左回到最左点。问最短路径的长度是多少?
输入文件包含多组数据。
每一组数据的第1行包含一个整数n (1<=n<=1000),表示点的数量。接下来的n行,每行包含两个浮点数(double) xi,yi,表示一个点的坐标为(xi,yi)。
对于每一组测试数据,输出一个两位小数,表示你计算出的最短距离。
| 样例输入 | 样例输出 |
|
3 |
6.47 |
<题目类型:双调欧几里得旅行商问题>
1.首先需要将原问题转化为,两个人A、B同时从最左边的点出发,一起严格向最右点走,且经过所有点一次(除了最左点和最右点)。这两个问题具有等价性。
2.先自然想到用dp(i,j)表示A走到i,B走到j时的状态还需要走多远到终点(注意表示的是还有多少到终点,所以其结果与前面怎么走的无关),那么可以证明dp(i,j)==dp(j,i);这里有的人可能会疑惑为什么会相等,刚刚说过dp(i,j)表示已经达到这个状态后还需要走多远到达终点,与怎么到达这个状态的并没有关系,所以dp(i,j)和dp(j,i)只是两个人角色对换了而已。
3.想到这一步之后,会出现一个问题,就是dp(i,j)无法知道i、j之间的某些点是否已经走过了,所以我们需要进一步思考,刚刚我们提到,dp(i,j)==dp(j,i),那么我们就可以始终让i>=j(等于只有终点和起点达到)。如果j>i了,只需要交换A、B的角色即可,即将i换为j,j换为i。
4.有了这个条件之后,我们就可以规定dp(i,j)规定为:A在i,B在j(i>=j)且i之前的所有点都走过了,这样也不会漏解,为什么呢?我们的自然的方法中,之所以i~j之间有点不知道走过了没,就是因为我们允许A连续走了多步,比如A从P1->P5->P6,而B可能从P1->P2。所以P3,P4我们不知道有没有被A或者B走到,因为我们只知道A走到了P6而B走到了P2。但是你明显发现了,在刚刚那个例子中,P3、P4之后必须要被B走到。所以我们改进的dp(i,j)中可以让A和B一格一格走,要么A走,要么B走(其实只是让顺序变化了一下而已)。
5.有了刚刚的论证,我们的状态转移就变成了下面这样:
dp[i][j]=min(DP(i+1,j)+dist(i,i+1),DP(i+1,i)+dist(j,i+1));
即要么A走,要么B走,如果A走的话,那么走到状态dp(i+1,j);如果B走,那么走到状态dp(i,i+1)到要求前面大于后面,所以dp(i,i+1)==dp(i+1,i)即可。注意dist(i,j)表示i-j的距离。
#include<iostream>
#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std;
struct point
{
double x;
double y;
};
point p[1010];
double dp[1010][1010];
double dis[1010][1010];
bool cmp(point a,point b)
{
return a.x<b.x;
}
double dist(int i,int j)
{
if(dis[i][j]>=0)
return dis[i][j];
return dis[i][j]=sqrt((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y));
}
double DP(int i,int j)
{
if(dp[i][j]>=0)
return dp[i][j];
dp[i][j]=min(DP(i+1,j)+dist(i,i+1),DP(i+1,i)+dist(j,i+1));
return dp[i][j];
}
int main()
{
int n;
while(scanf("%d",&n)!=EOF)
{
for(int i=0;i<1010;i++)
for(int j=0;j<1010;j++)
{
dis[i][j]=-1.0;
dp[i][j]=-1.0;
}
for(int i=0;i<n;i++)
cin>>p[i].x>>p[i].y;
sort(p,p+n,cmp);
for(int j=0;j<n;j++)
dp[n-2][j]=dist(n-2,n-1)+dist(j,n-1);
printf("%.2lf\n",DP(0,0));
}
return 0;
}
有一首很热门的曲子,叫做"劲歌金曲"。这首歌实际上是37首歌的集合,长达11分18秒。为什么它这么热门呢?假设你在KTV唱歌时只有15秒就到包场时间了,由于KTV不会在唱歌中途来叫停,你应该尽快选另一首曲子来延长时间。如果这时你选了劲歌金曲,那么你就会得到额外663秒的时间......~\(≧▽≦)/~
现在你还有一些时间,但是你准备制定一个计划。同时你要满足以下规则:
1>一首歌最多只能唱一遍(包括 劲歌金曲 )
2>对于一首长度为t的歌,要么唱完t时间,要么不唱
3>一首歌结束后,立即唱下一首(中间没有停顿)
你的目标很简单,唱尽可能多的歌,尽可能晚的离开KTV根据第三条规则,这也会使我们唱最多的歌)。
输入文件的第一行包含一个整数T (1<=T<=30),表示有T组测试数据。
每一组测试数据以两个整数n和t (1≤n≤50,1≤t≤10^9)开始,分别表示歌曲的数量(不包括劲歌金曲)和剩余的时间。接下来的一行包含n个整数,分别表示这n首歌的时间长度 (以秒(s)为单位,每首歌的长度不超过3分钟)。
输入数据保证,所有歌(包括劲歌金曲)的时间总和一定超过t。
对于每一组数据,给出最大的歌曲数和唱歌的总时间。
| 样例输入 | 样例输出 |
|
2 |
Case 1: 2 758 |
<样例解释>
对于第一组数据,先唱80秒长的第三首,再唱678秒长的劲歌金曲。
对于第二组数据,先唱第一首和第二首(总共99秒),此时还剩余最后1秒,我们再唱劲歌金曲(678秒)。如果我们先唱第一首和第三首(总共100秒),我们就没有时间唱劲歌金曲了。
每首歌最多选一次,由条件180n+678>T可知最大T=9678s,可以转化为0-1背包的问题:
1.状态d[i][j]表示:在当前剩余时间为j的情况下,从i,i+1,…,n中能选出歌的最大数目。
状态转移方程:d[i][j]=max{ d[i+1][j] , d[i+1][j-t[i]]+1 },( j-t[i]>0 );其中d[i+1][j]表示第i首歌未选时所选歌的最大数目,d[i+1][j-t[i]]+1表示第i首歌被选择后所选歌的最大数目。注意当 j-t[i]<=0 时 ,即剩余时间不大于0时,第i首歌不能选,此时d[i][j]=d[i+1][j];
边界条件是:i>n,d[i][j]=0;
2.由于题目要求在所点歌数目最大的情况下尽量保证唱歌的时间最长,那么同样可以转化成0-1背包问题,但是d[i][j]要先计算:
状态song[i][j]表示:在当前剩余时间为j的情况下,从i,i+1,…,n中所选出歌累计的最长时间。
状态转移跟随d[i][j]进行:令v1=d[i+1][j](即不选第i首歌),v2=d[i+1][j-t[i]]+1(选择第i首歌)
如果:
1) v2>v1, 说明第i首歌必须点,song[i][j]=song[i+1][j-t[i]]+t[i];
2) v2==v1, song[i][j]=max{song[i+1][j],song[i+1][j-t[i]]+t[i]};
3) v2<v1, 说明第i首歌一定不能点,song[i][j]=song[i+1][j];
逆序递推,答案是d[1][T]和song[1][T]。
#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int INF=-100000000; const int maxn=50; const int maxt=10000; int t[maxn+5]; int d[maxn+5][maxt]; int song[maxn+5][maxt]; int n,T; int main() { int Case; scanf("%d",&Case); for(int tt=1;tt<=Case;tt++) { scanf("%d%d",&n,&T); memset(t,0,sizeof t); for(int i=1;i<=n;i++) scanf("%d",&t[i]); memset(d,0,sizeof d); memset(song,0,sizeof song); for(int j=T;j>=0;j--) { if(j-t[n]>0) song[n][j]=t[n]; else song[n][j]=0; } for(int i=n;i>=1;i--) for(int j=T;j>0;j--) { int v1,v2; v1=d[i+1][j]; if(j-t[i]<=0) v2=INF; else v2=d[i+1][j-t[i]]+1; d[i][j]=max(v1,v2); if(v2>v1) song[i][j]=song[i+1][j-t[i]]+t[i]; else if(v2==v1) song[i][j]=max(song[i+1][j],song[i+1][j-t[i]]+t[i]); else song[i][j]=song[i+1][j]; } int num=d[1][T]+1; int len=song[1][T]+678; printf("Case %d: %d %d\n",tt,num,len); } return 0; }
你将要为一个会议大厅设计一个照明系统。在做了一些调查和计算之后,你发现有一个节能的设计能满足大厅的照明需求。根据这一设计,你需要n种不同功率的电灯。由于电流调节需要,所有的电灯都需要被通过相同的电流,因此,每一种灯都有对应的额定电压。现在,你已经知道了每一种电灯的数量和单位成本。但问题来了,你将要为所有类别的灯泡买同样的电源。事实上,你也可以为每一种灯泡单独买一种电源(我们认为:一个电源可以为无数个额定电压为电源电压的电灯供电)来完成设计。但是公司财务部很快发现他们可以通过删除一些电源并更换高功率的灯泡。你当然不能把灯泡换成低功率的,因为这样就会使大厅的一部分不能得到照明。你更关心的是节约金钱而不是节约能源,因此你要重新设计一个系统(将一些低电压灯泡更换为高电压灯泡),来使价格最便宜。
有多组数据。
每一组数据以一个整数n (1<=n<=1000),表示灯泡的种类。接下来的n行每一行表示一种灯泡的信息,一行包含4个整数:额定电压V (1<=V<=132000),满足所需电压的电源的单价K (1<=K<=1000),灯泡的单价C (1<=C<=10),需要的灯泡数量L (1<=L<=100)。
当n=0时,输入数据结束。
对于每一组数据,输出可能的最小花费。
| 样例输入 | 样例输出 |
|
3 |
778 |
首先需要明确一种灯泡要么全部换,要么不换。如果换一部分的话,首先电源费用得不到节约,那么节约的部分就只来自于换的那部分灯泡,既然可以节约钱干嘛不干脆全部换了呢?所以要么全换,要么不换。然后我们的算法就是先按照V排序,然后cost[i]表示解决前 i 种灯泡的最优解,那么转移方程是枚举j<i,将j之前的保持最优解cost[j]不变,j之后的全部变成i种灯泡。开始有一个疑问是:会不会漏解,为什么没有枚举替换j之前的不连续的一部分?后来发现,这个问题其实不存在,因为i之前的灯泡肯定是越后面的花费越大,因为如果前面的花费反而更大的话,大可以转换为后面的灯泡。
#include<iostream> #include<algorithm> #include<cstring> #include<cstdio> #define INF 0x3f3f3f3f #define MAXN 1010 using namespace std; struct node { int v,k,c,l; }; node light[MAXN]; bool cmp(node a,node b) { return a.v<b.v; } int num[MAXN]; int cost[MAXN]; int main() { int n; while(scanf("%d",&n)!=EOF&&n!=0) { for(int i=1;i<=n;i++) cin>>light[i].v>>light[i].k>>light[i].c>>light[i].l; sort(light+1,light+n+1,cmp); num[0]=0; for(int i=1;i<=n;i++) { num[i]=num[i-1]+light[i].l; } cost[0]=0; for(int i=1;i<=n;i++) { cost[i]=INF; for(int j=0;j<=i;j++) cost[i]=min(cost[i],cost[j]+(num[i]-num[j])*light[i].c+light[i].k); } cout<<cost[n]<<endl; } return 0; }
输入两个长度分别为n和m(n,m≤5000)的颜色序列,要求按序列合并成同一个序列,即每次可以把一个序列开头的颜色放到新序列的尾部。例如,两个颜色序列GBBY和YRRGB,至少有两种合并结果:GBYBRYRGB和YRRGGBBYB。对于每个颜色c来说,其跨度L(c)等于最大位置和最小位置之差。例如,对于上面两种合并结果,每个颜色的L(c)和所有L(c)的总和如图所示。你的任务是找一种合并方式,使得所有L(c)的总和最小。(注:该英文翻译来自《算法竞赛入门经典(第2版)》)
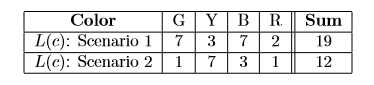
输入文件包含了T组测试数据,T在输入数据的第1行会给出。
每一组测试数据包含两行字符串,各代表一个颜色序列。在字符串中,颜色用大写英文字母表示。
输入数据保证:每组数据中出现的颜色数不超过26,每一个颜色序列的长度不超过5000。
对于每一组测试数据,输出一个整数,表示L(c)的总和的最小值。
| 样例输入 | 样例输出 |
|
2 |
10 |
对于两个颜色序列p和q,设d(i,j),表示p拿前i个字符,q拿前j个字符所要的代价。
由于n,m<=5000,二维数组改成滚动数组。
这个时候,不是等到一个颜色全部移动完了之后再算跨度,而是,只要多少种颜色已经开始但尚未结束,就L(c)+1;
重点在于求代价C。首先计算全部移动q,只要是该字符开头,代价就加一,但是如果刚好是最后一个就恢复。然后再推数组p时,就可以直接利用已经计算好的c代价数组,只需要根据它更新由于i的加入而增加的代价。
#include<iostream> #include<algorithm> #include<cstring> #include<cstdio> #define maxn 5005 #define INF 0x3f3f3f3f using namespace std; char p[maxn],q[maxn]; int sp[26],ep[26],sq[26],eq[26]; int d[2][maxn],c[2][maxn]; int main() { int t; scanf("%d",&t); while(t--) { scanf("%s%s",p+1,q+1); int n=strlen(p+1); int m=strlen(q+1); for(int i=1;i<=n;i++) p[i]-=‘A‘; for(int i=1;i<=m;i++) q[i]-=‘A‘; for(int i=0;i<26;i++) { sp[i]=sq[i]=INF; ep[i]=eq[i]=0; } for(int i=1;i<=n;i++) { sp[p[i]]=min(sp[p[i]],i); ep[p[i]]=i; } for(int i=1;i<=m;i++) { sq[q[i]]=min(sq[q[i]],i); eq[q[i]]=i; } memset(c,0,sizeof(c)); memset(d,0,sizeof(d)); int t=1; for(int i=0;i<=n;i++) { for(int j=0; j<=m;j++) { if(!i&&!j) continue; int v1=INF,v2=INF; if(i) v1=d[t^1][j]+c[t^1][j]; if(j) v2=d[t][j-1]+c[t][j-1]; d[t][j]=min(v1, v2); if(i) { c[t][j]=c[t^1][j]; if(sp[p[i]]==i&&sq[p[i]]>j) c[t][j]++; if(ep[p[i]]==i&&eq[p[i]]<=j) c[t][j]--; } else if(j) { c[t][j]=c[t][j-1]; if(sq[q[j]]==j&&sp[q[j]]>i) c[t][j]++; if(eq[q[j]]==j&&ep[q[j]]<=i) c[t][j]--; } } t^=1; } printf("%d\n",d[t^1][m]); } return 0; }
你的任务是替一家叫Analog Cutting Machinery (ACM)的公司切割木棍。 切割木棍的成本是根据木棍的长度而定。 而且切割木棍的时候每次只切一段。
很显然的,不同切割的顺序会有不同的成本。 例如: 有一根长10公尺的木棍必须在第2、4、7公尺的地方切割。 这个时候就有几种选择了。你可以选择先切2公尺的地方, 然后切4公尺的地方,最后切7公尺的地方。这样的选择其成本为:10+8+6=24。 因为第一次切时木棍长10公尺,第二次切时木棍长8公尺,第三次切时木棍长6公尺。 但是如果你选择先切4公尺的地方,然后切2公尺的地方,最后切7公尺的地方, 其成本为:10+4+6=20,这成本就是一个较好的选择。
你的老板相信你的电脑能力一定可以找出切割一木棍所需最小的成本。
一句话题意:给定一根已知长度的木棍,给定n个切割点,要求按照切割点切割木棍,花费按照切割的木棍长度计算,例如有一根长10的木棍,切割点为2、4、7,如果按照2、4、7的顺序切割,花费将是10 + 8 + 6 = 24,如果按照4、2、7的顺序切割,那么花费将是10 + 4 + 6 = 20,切割顺序可以任意,要求花费最小。
包含多组测试数据。
对于每组测试数据:第1行包含一个正整数l (l<1000),表示木棍的总长度。第2行给出正整数n (n<50),表示切割点的数量。第3行按升序给出n个正整数ci (0<ci<l),表示每一个切割点的位置。
当l=0时,输入数据结束。
对于每一组测试数据,输出完成切割的最小花费。输出格式见样例。
| 样例输入 | 样例输出 |
|
100 |
The minimum cutting is 200. |
比较典型的动态规划题目,根据题意找到状态转移公式就好了:dp[i][j]=max{dp[i][k]+dp[k][j]+len[j]-len[i]|i<k<j}
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<algorithm> #include<cstring> const int INF = 0x3f3f3f3f; using namespace std; int dp[100][100]; int num[100]; int main() { int len,n; while(scanf("%d",&len)&&len) { scanf("%d",&n); memset(dp,0,sizeof(dp)); for(int i=1;i<=n;i++) scanf("%d",&num[i]); num[0]=0; num[n+1]=len; int minn,p; for(int i=1;i<=n+1;i++) { for(int j=0;j+i<=n+1;j++) { p=j+i; minn=INF; for(int k=j+1;k<p;k++) { int temp=dp[j][k]+dp[k][p]+num[p]-num[j]; if(temp<minn) minn=temp; } if(minn!=INF) dp[j][p]=minn; } } printf("The minimum cutting is %d.\n",dp[0][n+1]); } return 0; }
我们认为一个括号序列是有规律的,需满足以下条件:
1.一个空的序列是有规律的;
2.如果S是有规律的括号序列,那么(S)和[S]都是有规律的括号序列;
3.如果A和B都是有规律的括号序列,那么AB也是有规律的括号序列。
举个例子,一下的所有括号序列都是有规律的:
(), [], (()), ([]), ()[], ()[()]
而以下的括号序列都不是:
(, [, ), )(, ([)], ([(]
给出一个包含‘(‘, ‘)‘, ‘[‘, 和 ‘]‘的序列S,你要找到最短的有规律的括号序列,使S成为其字串。
输入文件最多包含100个括号字符(仅包含‘(‘, ‘)‘, ‘[‘, 和 ‘]‘)。
输出找到的括号序列。
| 样例输入 | 样例输出 |
| ([(] | ()[()] |
用DP求最少需要括号数:以p从1到n(字符串长度),记录下从i到i+p需要添加的最少括号数f[i][j],同时记录下中间需要添加括号的位置pos[i][j]——为-1表示不需要添加。
#include<cstdio> #include<cstring> #define MAXN 120 const int INF=0x7fffffff; int f[MAXN][MAXN],pos[MAXN][MAXN]; char s[MAXN]; int n; int DP() { n=strlen(s); memset(f,0,sizeof(f)); for(int i=n;i>0;i--) { s[i]=s[i-1]; f[i][i]=1; } int tmp; for(int p=1;p<=n;p++) { for(int i=1;i<=n-p;i++) { int j=i+p; f[i][j]=INF; if((s[i]==‘(‘&&s[j]==‘)‘)||(s[i]==‘[‘&&s[j]==‘]‘)) { tmp=f[i+1][j-1]; if(tmp<f[i][j]) f[i][j]=tmp; } pos[i][j]=-1; for(int k=i;k<j;k++) { tmp=f[i][k]+f[k+1][j]; if(tmp<f[i][j]) { f[i][j]=tmp; pos[i][j]=k; } } } } return f[1][n]; } void print(int beg,int End) { if(beg>End) return ; if(beg==End) { if(s[beg]==‘(‘||s[beg]==‘)‘) printf("()"); else printf("[]"); } else { if(pos[beg][End]==-1) { if(s[beg]==‘(‘) { printf("("); print(beg+1,End-1); printf(")"); } else { printf("["); print(beg+1,End-1); printf("]"); } } else { print(beg,pos[beg][End]); print(pos[beg][End]+1,End); } } } int main() { scanf("%s",s); DP(); print(1,n); return 0; }
<这里有一个坑一点的变式:UVALive 2451,你可以改改这道题的代码再提交,随意感受一下>

#include<cstdio> #include<cstring> #include<string> #include<algorithm> #include<iostream> #include<cstdlib> #include<cmath> #define MAXN 120 using namespace std; const int INF=0x7fffffff; int f[MAXN][MAXN],pos[MAXN][MAXN]; char s[MAXN]; int n; void Clear() { memset(pos,0,sizeof(pos)); memset(s,0,sizeof(s)); n=0; } int DP() { n=strlen(s); memset(f,0,sizeof(f)); for(int i=n;i>0;i--) { s[i]=s[i-1]; f[i][i]=1; } int tmp; for(int p=1;p<=n;p++) { for(int i=1;i<=n-p;i++) { int j=i+p; f[i][j]=INF; if((s[i]==‘(‘&&s[j]==‘)‘)||(s[i]==‘[‘&&s[j]==‘]‘)) { tmp=f[i+1][j-1]; if(tmp<f[i][j]) f[i][j]=tmp; } pos[i][j]=-1; for(int k=i;k<j;k++) { tmp=f[i][k]+f[k+1][j]; if(tmp<f[i][j]) { f[i][j]=tmp; pos[i][j]=k; } } } } return f[1][n]; } void print(int beg,int End) { if(beg>End) return ; if(beg==End) { if(s[beg]==‘(‘||s[beg]==‘)‘) printf("()"); else printf("[]"); } else { if(pos[beg][End]==-1) { if(s[beg]==‘(‘) { printf("("); print(beg+1,End-1); printf(")"); } else { printf("["); print(beg+1,End-1); printf("]"); } } else { print(beg,pos[beg][End]); print(pos[beg][End]+1,End); } } } int main() { int num; scanf("%d",&num); getchar(); for(int i=1;i<=num;i++) { Clear(); gets(s); gets(s); DP(); print(1,n); if(i!=num) printf("\n\n"); else printf("\n"); } return 0; }
按照顺时针或者逆时针的顺序给出多边的点,要将这个多边形分解成n-2个三角形,要求使得这些三角行中面积最大的三角形面积尽量小,求最小值。
输入文件包含多组数据。输入文件的第1行包含一个整数n,表示有n组数据。
对于每一组数据,第1行包含一个整数m (2<m<50),表示该多边形有m个顶点。接下来的m行,每行包含两个整数x和y (0<=x,y<=10000),表示一个顶点的坐标。
对于每一组数据,输出面积的最小值,答案保留一位小数。
| 样例输入 | 样例输出 |
|
1 |
9.0 |
状态很好想,dp[i][j]表示从第i个点到第j个点,划分成j-i-1个三角形的最优解,然后每次转移时,枚举长度和左边界始点,那么根据长度和左边界点就可以知道右边界点,然后枚举左边界和右边界中间的点k,dp[i][j] = min(dp[i][j], max(max(dp[i][k], dp[k][j]), Area(i, k, j)).但是有一个问题,即i,k,j三点围成的三角形是否符合要求,判断的条件即为是否存在除i,k,j三点外的一点位于三角形中,有面积法判断。
#include<cstdio> #include<cstring> #include<cmath> #include<algorithm> using namespace std; const int N=100; const double INF=0x3f3f3f3f3f3f; const double eps=1e-9; struct point { double x,y; void get() { scanf("%lf%lf",&x,&y); } }p[N]; int n; double dp[N][N]; double area(point a,point b,point c) { return fabs((b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y))/2; } bool judge(int a,int b,int c) { double cur=area(p[a],p[b],p[c]); for(int i=0;i<n;i++) { if(i==a||i==b||i==c) continue; double tmp=area(p[a],p[b],p[i])+area(p[b],p[c],p[i])+area(p[c],p[a],p[i]); if (fabs(tmp-cur)<eps) return false; } return true; } double solve () { for(int i=0;i<2;i++) { for(int j=0;j<n;j++) dp[j][(j+i)%n]=0; } for(int i=0;i<n;i++) dp[i][(i+2)%n]=area(p[i],p[(i+1)%n],p[(i+2)%n]); for(int k=3;k<n;k++) { for(int i=0;i<n;i++) { int t=(i+k)% n; dp[i][t]=INF; for(int j=(i+1)%n;j!=t;j=(j+1)%n) { if(judge(i,t,j)) dp[i][t]=min(dp[i][t],max(max(dp[i][j],dp[j][t]),area(p[i],p[j],p[t]))); } } } double ans=INF; for(int i=0;i<n;i++) ans=min(ans,dp[i][(i+n-1)%n]); return ans; } int main () { int cas; scanf("%d",&cas); while(cas--) { scanf("%d",&n); for(int i=0;i<n;i++) p[i].get(); printf("%.1lf\n",solve()); } return 0; }
世界危机发生了,工人们请求加薪。一个老板和n个员工组成树状结构,每个员工都有自己的唯一上司,Boss的编号为0,员工1~n,工人们打算签署一个志愿书给老板,但无法跨级,当一个中级员工(非是工人的员工)的直属下属中不小于T%的人签字时,他也会签字并且递给他的直属上司,问:要让Boss收到请愿书至少需要多少个工人签字?
输入文件包含多组数据,每一组测试数据占两行。
对于每一组测试数据:第1行包含两个整数N和T (1≤N≤10^5,1≤T≤100),其中N表示公司里的员工数(不包括Boss),T的含义见题目描述;第2行包含N个整数Bi (0<=Bi<=i-1),表示编号为i的员工的直系Boss是编号为Bi的员工。
当N=0且T=0时,输入文件结束。
对于每一组测试数据,输出需要签字的最少员工数。
| 样例输入 | 样例输出 |
|
3 100 |
3 |
设d[u]表示让u给上级发信最少需要多少个工人。假设u有k个子节点,则至少需要c=(k*T-1)/100+1个直接下属发信才行。把所有子节点的d值从小到大排序,前c个加起来即可。最终答案是d[0]。
#include<vector> #include<algorithm> #include<cstring> #include<cstdio> #include<cmath> using namespace std; const int maxn=100000+5; int n,t; vector<int> sons[maxn]; int dp(int u) { if(sons[u].empty()) return 1; vector<int> d; int k=sons[u].size(); for(int i=0;i<k;i++) d.push_back(dp(sons[u][i])); sort(d.begin(),d.end()); int c=(k*t-1)/100+1; int ans=0; for(int i=0;i<c;i++) ans+=d[i]; return ans; } int main() { int temp; while(scanf("%d%d",&n,&t)&&(n||t)) { for(int i=0;i<=n;i++) sons[i].clear(); for(int i=1;i<=n;i++) { scanf("%d",&temp); sons[temp].push_back(i); } int ans=dp(0); printf("%d\n",ans); } return 0; }
N台电脑由N-1条连线连接,使得任意两台电脑都能够通过一条道路联系,这样就形成了网络。如果两台电脑间有一条线连接,那么我们说这两台电脑相邻。所有与一台电脑相邻的电脑组成的集合,我们称之为邻居。为了能够快速地存取接收大量的信息,我们需要将一些电脑变为服务器,来向它所有的邻居提供资源。如果在一个网络中,所有的用户(即不是服务器的电脑)都被恰好一个服务器提供资源,我们就认为这个网络形成了完美服务。现在我们定义,使一个网络形成完美服务所需要的最少的服务器的数量,叫做"完美服务数"。
我们假设有N台电脑,且将电脑从1~N编号。例如Figure 1所示的网络由6台电脑组成,其中的黑点表示服务器,白点表示用户。在Figure 1(a)中,3号和5号服务器没有形成完美服务,因为4号用户同时被两个服务器覆盖到了。而在Figure 1(b)中,3号和4号服务器就形成了完美服务,这个例子中的"完美服务数"就等于2。
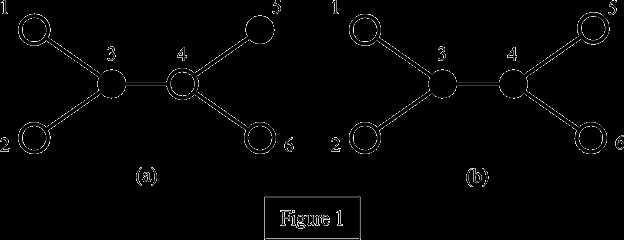
你的任务是写一个程序计算出"完美服务数"。
输入文件包含多组数据。
对于每一组数据:第一行包含一个正整数N (1<=N<=10000),表示网络中的电脑数。接下来的N-1行,每一行都包含两个正整数Ai和Bi,表示Ai和Bi是相邻的。第N+1行的"0"表示第一组数据的结束,接着开始输入下一个数据。当一组数据的末尾给出"-1"时,表示全部的输入数据结束。
对于每一组测试数据,输出计算出的"完美服务数"。
| 样例输入 | 样例输出 |
|
6 |
2 |
dp[i][0]表示i是服务器并且以i为根的子树都被覆盖的情况下服务器的最少点数
dp[i][1]表示i不属于服务器,且以i为根的子树都被覆盖,且i被其中不少于一个子节点覆盖的情况下服务器的最少点数
dp[i][2]表示i不属于服务器,且以i为根的子树都被覆盖,且i没被子节点覆盖的情况下服务器的最少点数
dp[i][0]=1+sum(min(dp[u][0],dp[u][2]))
dp[i][1]=INF 当i没有子节点
dp[i][1]=sum(min(dp[u][0],dp[u][1]))+inc 当i有子节点
inc=0若sum(min(dp[u][0],dp[u][1]))包含某个dp[u][0]
否则inc=min(dp[u][0]-dp[u][1])
dp[i][2]=sum(dp[u][1])
结果即为min(dp[1][0],dp[1][1])
#include<cstdio> #include<iostream> #include<cstring> #define maxn 11111 #define INF 0x3f3f3f3f #define ll long long using namespace std; struct Edge { int to; int next; }edge[2*maxn]; int n,head[maxn],tot; int dp[maxn][3]; void init() { tot=0; memset(head,-1,sizeof(head)); for(int i=0;i<maxn;i++) dp[i][1]=INF; } void add(int u,int v) { edge[tot].to=v; edge[tot].next=head[u]; head[u]=tot++; } void DP(int u,int fa) { dp[u][0]=1,dp[u][2]=0; int sum=0,inc=INF,flag=0; for(int i=head[u];~i;i=edge[i].next) { int v=edge[i].to; if(v==fa) continue; DP(v,u); dp[u][0]+=min(dp[v][0],dp[v][2]); if(dp[v][0]<=dp[v][1]) sum+=dp[v][0],flag=1; else sum+=dp[v][1],inc=min(inc,dp[v][0]-dp[v][1]); if(dp[v][1]!=INF&&dp[u][2]!=INF) dp[u][2]+=dp[v][1]; else dp[u][2]=INF; } if(inc!=INF&&!flag) dp[u][1]=INF; else { dp[u][1]=sum; if(!flag) dp[u][1]+=inc; } } int main() { while(~scanf("%d",&n)) { init(); int u,v,t; for(int i=1;i<n;i++) { scanf("%d%d",&u,&v); add(u,v); add(v,u); } DP(1,1); int ans=min(dp[1][0],dp[1][1]); printf("%d\n",ans); scanf("%d",&t); if(t!=0) break; } return 0; }
Frank从个人投资者获得了c美元的资金,可用于m天的投资。
Frank可以对n支股票进行投资。对于每一支股票:都有一个交易上限si,表示一天最多能交易的股数;还有一个上限ki,表示Frank最多可持有的股数。对于所有种类的股票,同样有一个上限k表示Frank可同时持有的最大股数。
股票的交易还满足一下要求:
1>一天最多只能进行一次交易(你也可以不交易);
2>若要对第i支股票进行买进或卖出,只能一次性买或卖Si股;
3>所有的交易都是在Frank有足够的资金的条件下完成的;
4>当m天过去后,Frank的资金必须全部转化为现金,不能放在股票市场里,(m天之内,股票必须全部卖出)。
现在,给出每一支股票的每一天的价格,要求你计算出Frank能回收的资金的最大值,并给出每一天的具体的操作方法。
第1行:包含四个数c,m,n,k:c (0.01 ≤ c ≤ 100 000 000.00)表示一开始持有的资金,最多两位小数;m (1 ≤m ≤ 100)表示可以交易的天数;n (1 ≤ n ≤ 8)表示股票的种数;k (1 ≤ k ≤ 8)表示所有股票的最多持有的股数。
接下来的2n行:描述每一支股票的信息(一支股票占2行)。对于每一支股票:第1行:包含股票名称(一个五位以内的大写字母组成的字符串),si(1 ≤ si ≤ 1 000 000,一天的最大交易量),ki(1 ≤ ki ≤ k,该股票的最大持有股数);第2行:包含m 个小数(0.01<=m<=999.99,二位小数以内),表示股票每一天的价格。
输出文件包含m+1行。第1行:回收资金的最大值;第2~m+1行,每一天的操作。具体格式见样例。
| 样例输入 | 样例输出 |
144624.00 9 5 3
IBM 500 3
97.27 98.31 97.42 98.9 100.07 98.89 98.65 99.34 100.82
GOOG 100 1
467.59 483.26 487.19 483.58 485.5 489.46 499.72 505 504.28
JAVA 1000 2
5.54 5.69 5.6 5.65 5.73 6 6.14 6.06 6.06
MSFT 250 1
29.86 29.81 29.64 29.93 29.96 29.66 30.7 31.21 31.16
ORCL 300 3
17.51 17.68 17.64 17.86 17.82 17.77 17.39 17.5 17.3
|
151205.00
BUY GOOG
BUY IBM
BUY IBM
HOLD
SELL IBM
BUY MSFT
SELL MSFT
SELL GOOG
SELL IBM
|
一共有n天,把天数看作阶段,对于每一天,我们可以选择出手或买进一手股票,在最后一天必须将股票全部出手且求解最大钱数。
可以这样定义d[i][s]:表示第i天手中股票的状态为s时手中的最大钱数,采用刷表法更新d[i+1][s‘],s‘表示s经过出手或买进转移的状态。
问题就变成了如何表示状况s?采用n元组的形式。
但不能将一个n元组表示进d数组,这里的方法是离线dfs出全部状态并分别编号,得出状态与相连的关系buy_next与sell_next。那么d中的状态s就可以用一个整数表示了。
另外输出也有一定的技巧,用到了pre与opt数组,并用正负区别操作。
#include<cstring> #include<cstdio> #include<cmath> #include<algorithm> #include<cstdlib> #include<iostream> #include<map> #include<vector> #define maxn 110 #define INF 0X3F3F3F3F using namespace std; double C; int M,N,K; char name[10][maxn]; int k[maxn]; double d[10][maxn]; map <vector<int>,int>ID; vector <vector<int> >states; double bn[15000][10]; double sn[15000][10]; double dp[maxn][15000]; int opt[maxn][15000],pre[maxn][15000]; void dfs(int day,vector<int>& lots,int tot) { if(day==N) { ID[lots]=states.size(); states.push_back(lots); return; } for(int i=0;i<=k[day]&&i+tot<=K;i++) { lots[day]=i; dfs(day+1,lots,tot+i); } } void ud(int day,int s,int s2,double v,int o) { if(v>dp[day+1][s2]) { dp[day+1][s2]=v; opt[day+1][s2]=o; pre[day+1][s2]=s; } } void print_ans(int day,int s) { if(day==0) return; print_ans(day-1,pre[day][s]); if(opt[day][s]==0) printf("HOLD\n"); else if(opt[day][s]>0) printf("BUY %s\n",name[opt[day][s]-1]); else printf("SELL %s\n",name[-opt[day][s]-1]); } int main() { while(scanf("%lf %d %d %d",&C,&M,&N,&K)!=EOF) { double temp; for(int i=0;i<N;i++) { scanf("%s %lf %d",name[i],&temp,&k[i]); for(int j=0;j<M;j++) { scanf("%lf",&d[i][j]); d[i][j]*=temp; } } ID.clear(); states.clear(); vector<int>lots(N); dfs(0,lots,0); for(unsigned int s=0;s<states.size();s++) { int tot=0; for(int i=0;i<N;i++) { bn[s][i]=sn[s][i]=-1; tot+=states[s][i]; } for(int i=0;i<N;i++) { if(states[s][i]<k[i]&&tot<K) { vector<int> news=states[s]; news[i]++; bn[s][i]=ID[news]; } if(states[s][i]>0) { vector<int> news=states[s]; news[i]--; sn[s][i]=ID[news]; } } } for(int day=0;day<=M;day++) for(unsigned int s=0;s<states.size();s++) dp[day][s]=-INF; dp[0][0]=C; for(int day=0;day<M;day++) for(unsigned int s=0;s<states.size();s++) { double v=dp[day][s]; if(v<-1) continue; ud(day,s,s,v,0); for(int i=0;i<N;i++) { if(bn[s][i]>=0&&v>=d[i][day]-1e-3) ud(day,s,bn[s][i],v-d[i][day],i+1); if(sn[s][i]>=0) ud(day,s,sn[s][i],v+d[i][day],-i-1); } } printf("%.2lf\n",dp[M][0]); print_ans(M,0); } return 0; }
你想学着玩跳舞机。跳舞机的踏板上有四个箭头:上、下、左、右。当舞曲开始时会有一些箭头往上移动。当向上移动的箭头与顶部的箭头模板重合时,你需要用脚踩一下踏板上的相同箭头。不需要踩箭头时,踩箭头不会受到惩罚,但当需要踩箭头时必须踩一下,哪怕已经有一只脚放在了该箭头上。很多舞曲速度很快,需要来回倒腾步子。因此要写一个程序,来选择最轻松的踩踏方式,使得消耗的能量最少。
将八分音符作为一个基本时间单位,每个时间单位要么需要踩一个箭头(不会同时要求踩两个箭头),要么什么都不需要踩。在任意时刻,你的左右脚应放在两个不同的箭头上,且每个时间单位内只有一只脚能动(移动 和/或 踩箭头),不能跳跃。另外,你必须面朝前方以看到屏幕(例如,你不能左脚放在右箭头上,右脚放在左箭头上)。
当你执行一个动作(移动或踩踏)时,消耗的能量这样计算:
◎如果这只脚上个时间单位没有任何动作,消耗1单位能量;
◎如果这只脚上个时间单位没有移动,消耗3单位能量;
◎如果这只脚上个时间单位移动到相邻箭头,消耗5单位能量;
◎如果这只脚上个时间单位移动到相对箭头,消耗7单位能量。
正常情况下,你的左脚不能放在右箭头上(或者反之),但有一种情况例外:如果你的左脚放在上箭头或下箭头,你可以用右脚踩左箭头,但是在你的右脚移出左箭头之前,你的左脚都不能移到另一个箭头上。右脚的情况以此类推。
一开始,你的左脚在左箭头上,右脚在右箭头上。


跳舞机踏板 跳舞机屏幕
输入文件最多包含100组数据,每组数据包含一个长度不超过70的字符串,即各个时间单位要踩的箭头。L和R分别表示左右箭头,U和D分别表示上下箭头,‘.‘表示不需要踩箭头。
输出应是一个长度和输入相同的字符串,表示每个时间单位执行动作的脚。L和R分别是左右脚,‘.‘表示不踩。
| 样例输入 | 样例输出 |
|
LRLRLLLLRLRLRRRRLLRRLRLDU...D...UUUUDDDD |
LRLRLLLLRLRLRRRRLLRRLRLRL...R...LLLLRRRR |
对于屏幕上的位置必须有一脚踩下,对两脚位置有所要求且根据脚的移动关系分配代价,求完成屏幕要求的情况下代价最小。
用状态d[i][a][b][s]表示已踩过i个命令,左右脚位置为ab,因为需要根据当前移动的脚是否刚移动过所以用s表示上次移动的脚。
状态转移方程: d[i][a][b][s]=min(d[i][ta][tb][s‘]+cost)
但注意到,expr是当前的移动,移动后转移到i+1且位置成为移动后的位置, 因此需要倒序枚举i,把i+1看作是 i 的子问题
原来char[]可以这么用。
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; #define MAXN 75 #define INF 0x3f3f3f3f struct NODE { int i,l,r,s; }path[MAXN][4][4][3]; char a[MAXN]; int dp[MAXN][4][4][3],n,buf; bool ok(int f,int l,int r,int to) { if (0==f) { if(to==r) return false; if(to==l) return true; if(2==r) return false; } else { if(to==l) return false; if(to==r) return true; if(3==l) return false; } return true; } int cost(int s,int now,int from,int to) { if(s!=now) return 1; if(from==to) return 3; if((from==0&&to==1)||(from==1&&to==0)) return 7; if((from==2&&to==3)||(from==3&&to==2)) return 7; return 5; } int dfs(int i,int l,int r,int s) { int& ans=dp[i][l][r][s]; NODE& p=path[i][l][r][s]; if(-1!=ans) return ans; if(i==n) return ans = 0; ans=INF; if(‘.‘==a[i]) { ans=min(ans,dfs(i+1,l,r,0)); p.i=i+1,p.l=l,p.r=r,p.s=0; for(int j=0;j<4;j++) { if(ok(0,l,r,j)) { buf=dfs(i+1,j,r,1)+cost(s,1,l,j); if(ans>buf) ans=buf,p.i=i+1,p.l=j,p.r=r,p.s=1; } if(ok(1,l,r,j)) { buf=dfs(i+1,l,j,2)+cost(s,2,r,j); if(ans>buf) ans=buf,p.i=i+1,p.l=l,p.r=j,p.s=2; } } return ans; } int to; switch(a[i]) { case ‘U‘:to=0; break; case ‘D‘:to=1; break; case ‘L‘:to=2; break; case ‘R‘:to=3; break; } if(ok(0,l,r,to)) { buf=dfs(i+1,to,r,1)+cost(s,1,l,to); if(ans>buf) ans=buf,p.i=i+1,p.l=to,p.r=r,p.s=1; } if(ok(1,l,r,to)) { buf=dfs(i+1,l,to,2)+cost(s,2,r,to); if(ans>buf) ans=buf,p.i=i+1,p.l=l,p.r=to,p.s=2; } return ans; } void pt(int i,int l,int r,int s) { if(n==i) return; NODE& p=path[i][l][r][s]; if(!p.s) printf("."); else if(p.s==1) printf("L"); else printf("R"); pt(p.i,p.l,p.r,p.s); } int main() { while(scanf("%s%*c",a)&&‘#‘!= a[0]) { n=strlen(a); memset(dp,-1,sizeof(dp)); dfs(0,2,3,0); pt(0,2,3,0); puts(""); } return 0; }
你有k个一模一样的水球,在一个n层楼的建筑物上进行测试,你想知道水球最低从几层楼往下丢可以让水球破掉。由于你很懒,所以你想要丢最少次水球来测出水球刚好破掉的最低楼层。(在最糟情况下,水球在顶楼也不会破)你可以在某一层楼丢下水球来测试,如果水球没破,你可以再捡起来继续用。
输入文件包含多组测试,每组测试为一行。每组测试包含两个整数k和n,(1<= k<=100而n是一个LL的整数(没错,这栋建筑物的确很高),最后一组k=0,n=0代表结束。
对于每次测试,输出在最糟情况下,测出水球破掉楼层的最少次数。如果他多于63次,就输出“More than 63 trials needed.”
| 样例输入 | 样例输出 |
|
2 100 |
14 |
定义f[i][j] 表示给i个水球和j次实验机会,将问题转化为最高能够测试到几层
则会有转移方程:f[i][j]=f[i][j-1]+f[i-1][j-1]+1;
后一部分是说选在第k层试第一次,如果摔破了,说明边界在下面的层中。所以说选的那个k层,k最大应该满足k<=f[i-1][j-1]+1; 因为要保证一旦水球在第k层摔坏了,下面的所有层都可以在还有i-1个球和j-1次机会时测出来;
前一部分表示选在k层试第一次,但是球并没有摔坏。这个时候最高就是在k层的基础上,加上 还有i个球和j-1次机会时能够再往上测几层~即f[i][j-1];
所以综上两部分,f[i][j]最大就等于f[i-1][j-1]+1+f[i][j-1];
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; long long f[110][65]; void init() { memset(f,0,sizeof(f)); for(int i=1;i<64;i++) for(int j=1;j<64;j++) f[i][j]=f[i][j-1]+1+f[i-1][j-1]; } int main() { init(); int k; long long n; while(scanf("%d%lld",&k,&n)!=EOF) { if(k==0) break; k=min(k, 63); bool ok=false; for(int i=0;i<=63;i++) { if(f[k][i]>=n) { printf("%d\n",i); ok=true; break; } } if(!ok) printf("More than 63 trials needed.\n"); } return 0; }
Ministry of Monuments公司设计了GWARR机器人来修理长城。而你的任务就是写一个程序来计算修理的最小花费。
我们把长城看作是一条直线,那么我们就可以通过一个整数(某一点到长城一端的距离)来描述长城上一点的位置。GWARR机器人被放置在长城上的某一个地方并且可以向两个方向匀速运动。计算中忽略修理过程的时间消耗。
输入文件包含多组测试数据。
对于每一组数据:第1行包含三个整数:n (1<=n<=1000),表示长城上需要修复的地方;v (1<=v<=100),表示机器人的单位速度;x (1<=x<=500000),表示GWARR的最初位置。接下来的n行描述每一个缺口的信息,每一行包含三个整数:xi (1<=xi<=500000),表示缺口的位置;ci (0<=ci<=50000),现在(也就是0时刻)修好这个缺口所需的花费;Δ (1<=Δ<=50000),表示每一个单位时间增加的花费。因此,如果在t个单位时间后修理一个缺口,那么花费就是 c+t*Δ 。
输入数据保证:不存在两个缺口位置重叠的情况;机器人的初始位置不会与任何一个缺口位置重合。
当n=v=x=0时,输入文件结束。
对于每一组数据,输出最小花费。题目保证最小花费的值不会超过1000000000。
| 样例输入 | 样例输出 |
|
3 1 1000 |
2084 |
要想最终代价最低,就不能跳跃着修复,也就是经过一段时间后已经修复好的破损应是一段连续区间。定义dp(i,j,k)表示修好(i,j)后机器人停留在k(0表示在左端,1表示在右端)端的费用。修复某处破损的代价虽然不是定值,但却是随着时间线性增长的,所以当修复完一处或一段破损时,修复其他破损的费用可以算出来,只需将其累加到当前状态即可,也可以视作修复某处破损产生的时间代价。状态转移方程:dp(i,j,1)=min(dp(i,j-1,0)+w1,dp(i,j-1,1)+w2) ;dp(i,j,0)=min(dp(i+1,j,0)+w3,dp(i+1,j,1)+w4) 其中,w1、w2、w3、w4为相应产生的时间代价与修复代价的和。
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> using namespace std; const int N=1005; const double inf=1e30; struct node { int x,c,dlt; }; node p[N]; int n,v,x; double dp[N][N][2],s[N]; bool cmp(node a,node b) { return a.x<b.x; } double dfs(int l,int r,int k) { if(dp[l][r][k]>-1.0) return dp[l][r][k]; if(l==r) { double t=fabs((double)x-(double)p[l].x)/(double)v; dp[l][r][k]=s[n]*t+p[l].c; return dp[l][r][k]; } if(k==0) { double a=dfs(l+1,r,0); double b=dfs(l+1,r,1); double t1=(double)(p[l+1].x-p[l].x)/(double)v; double t2=(double)(p[r].x-p[l].x)/(double)v; double d=s[l]+s[n]-s[r]; dp[l][r][k]=min(a+d*t1,b+d*t2)+(double)p[l].c; } else { double a=dfs(l,r-1,0); double b=dfs(l,r-1,1); double t1=(double)(p[r].x-p[l].x)/(double)v; double t2=(double)(p[r].x-p[r-1].x)/(double)v; double d=s[l-1]+s[n]-s[r-1]; dp[l][r][k]=min(a+d*t1,b+d*t2)+p[r].c; } return dp[l][r][k]; } int main() { while(~scanf("%d%d%d",&n,&v,&x)) { if(n+v+x==0) break; for(int i=1;i<=n;++i) scanf("%d%d%d",&p[i].x,&p[i].c,&p[i].dlt); sort(p+1,p+n+1,cmp); s[0]=0.0; for(int i=1;i<=n;++i) s[i]=s[i-1]+(double)p[i].dlt; memset(dp,-1.0,sizeof(dp)); printf("%d\n",(int)min(dfs(1,n,0),dfs(1,n,1))); } return 0; }
Bob有n根火柴。他可以用火柴摆出0~9任意一个数字,如下图所示:
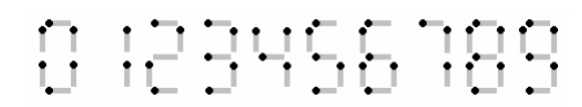
现在,给出一个整数m,要求用不超过n根火柴摆一个尽可能大的整数。
输入文件包含多组测试数据。每一组数据占一行,包含两个整数n (n<=100)和m (m<=3000),其含义见题目描述。
输入文件以一个单独的‘0‘结束。
对于每一组数据,输出计算出的答案;若无解,则输出-1。注意按样例所给出的格式输出。
| 样例输入 | 样例输出 |
|
6 3 |
Case 1: 111 |
<参考了 dawxy 大神的思路>
可以用dp[i][j]表示除以m余j的i位数最少需要多少火柴这个状态计算,转移方程是:用dp[i][j]+c[k]来更新dp[i+1][(j*10+k)%m](c[]是每个数字需要花费的火柴数量,k是当前枚举的数字)。可以避免高精度提高效率,但是怎么确定每一位上的数字都是什么呢,需要用dp[i][0]找到最大的i使得dp[i][0]不是INF(初始化dp[][]为INF),这样就可以确定这个最大数字有几位了(位数多的肯定比位数少的大),然后在计算每一位上最大可以是什么数字,从大到小枚举每一位上的数字,第一个使得sum+dp[i-1][s]+c[j]<=n的数字就是该位上的最大值(其中s是去掉这一位上的数字剩下的几位的余数为s时使得这个总的数字能被m整除)。
比如,m=7,并且已知当前数字位数为3,首先试着让最高位为9,如果可以摆出9ab这样的整数,那么一定是最大的,那么怎样确定能否摆出9ab呢?因为900%7=4,所以s,就是后两位‘ab‘%7应该等于3,(这里具体怎么算的下面再说),如果dp[2][3]+c[9]+sum<=n,(sum是已经确定的高位的数字的总花费),就说明火柴数量足够摆出9ab,否则最高位就不是9需要继续找,如果可以摆出那么重复这个过程直到算出每一位上的数字。还可以预处理计算出每个x00..这样数字%m的值用y数组保存,其实还是用到了一点高精度计算--大数取余。
现在就只有一个问题了,怎样算出s,就是已知当前整数为7ab%m = 0和700%m,求出ab%m的值,我计算了几个数字,找出了一个规律:
下面几位的余数s等于 m-当前这一位的数字x00..%m的值-v(前面所有已经确定的x00..%m之和)
比如:假设最大数字23450,m=7
20000%7=1,3000%7=4,400%7=1,50%7=1,0%7=0
2确定时 s(后4位%7)=(7-1-0)%7=6;v=0+1 验证:3450%7=6
23确定时 s(后3位%7)=(7-4-1)%7=2;v=1+4 验证:450%7=2
234确定时 s(后2位%7)=(7-1-5)%7=1;v=1+4+1 验证:50%7=1
2345确定时 s(后1位%7)=(7-1-6)%7=0;v=1+4+1+1 验证:0%7=0
需要注意一下v可能超过m,所以计算v时需要模m。计算s时可能为负数,需要先加m再模m
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; #define MAXM 3010 #define MAXN 105 #define MAXW 55 #define INF 0x3f3f3f3f const int c[10]={6,2,5,5,4,5,6,3,7,6}; int dp[MAXW][MAXM],y[10][MAXW][MAXM],ans[MAXW],sw,n,m; void sloved() { memset(ans,-1,sizeof(ans)); int sum=0,v=0; for(int i=sw;i>=1;i--) { for(int j=9;j>=0;j--) { if(sum+dp[i-1][(m-y[j][i-1][m]-v+m)%m]+c[j]<=n) { ans[i]=j; sum+=c[j]; v=(v+y[j][i-1][m])%m; break; } } if(-1==ans[i]) { if(n>=6) puts("0"); else puts("-1"); return; } } for(int i=sw;i>=1;i--) printf("%d",ans[i]); puts(""); } int main() { int Count=0; for(int i=1;i<=9;i++) { for(int k=1;k<=3000;k++) { int s=i; y[i][0][k]=i%k; for(int j=1;j<=50;j++) { s=s*10%k; y[i][j][k]=s; } } } while(~scanf("%d%*c",&n)&&n) { scanf("%d%*c",&m); memset(dp,0x3f,sizeof(dp)); dp[0][0]=0; int w=n>>1; for(int i=0;i<w;i++) { for(int j=0;j<m;j++) { if(INF==dp[i][j]) continue; for(int k=0;k<=9;k++) { if(dp[i][j]+c[k]<=n) dp[i+1][(j*10+k)%m]=min(dp[i+1][(j*10+k)%m],dp[i][j]+c[k]); } } } sw=-1; for(int i=w;i>=1;i--) { if(INF!=dp[i][0]) { sw=i; break; } } printf("Case %d: ",++Count); if(-1==sw) puts("-1"); else sloved(); } return 0; }
几个孩子在一棵老树旁占成一圈玩游戏。由于树很大,每个孩子只能看见离他近的人。
这个游戏由很多轮组成。在游戏的开始,一个随机的小孩会得到一张纸,如果这个小孩是男孩,会在纸上写一个‘B‘;如果是女孩,会在纸上写一个‘G‘。然后他任意选择一个方向(顺时针或逆时针),将纸递给在这个方向上与他相邻的人,新的人也会在纸上写下自己的性别,继续将纸递给另一个人(按照先前的方向)......就这样,这张纸从一个孩子交到另一个孩子手中,直到一个孩子宣布游戏结束。
举个例子,假设有5个孩子将树围起来,如Figure 1,。现在,若纸从Kid1开始向逆时针走,在Kid3停下,那么我们就会在纸上得到一个字符串"BBG"。
在N轮游戏后,我们会得到N张写有‘B‘和/或‘G‘的字符串的白纸。一个小孩会得到所有的这些纸,并且要算出至少有多少个小孩参与了游戏。我们知道在任意情况下,至少有两个小孩。写一个程序,计算这个最少的人数。
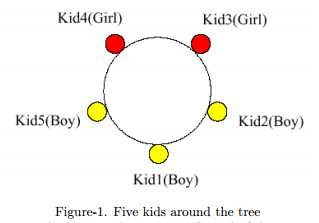
输入文件包含多组测试数据。
对于每一组数据:第1行包含一个整数N (2<=N<=16),表示总共有N个字符串;接下来的N行,每行包含一个由‘B‘和/或‘G‘组成的字符串,字符串的长度均不超过100。
当N=0时,输入数据结束。
对于每一组数据,输出可能的最少的孩子数。
| 样例输入 | 样例输出 |
|
3 |
9 |
我们可以在预处理时把所有相互包含的字符串合并,然后f[i][j][k] 表示当前字符串已经包含的字符串为i,并且以j结尾且其方向为k的最小值,然后每次枚举转移,注意最后一个字符串要处理一下它和第一个字符串的公共部分(因为是环),然后可能有一个字符饶了好几圈这种情况,这时我们最后一定可以把所有字符合并成最长的那一个,然后用kmp求下它的最小循环节输出就行了,注意所有答案都要和2取最大值。
#include<cstring> #include<cstdio> #include<cstdlib> #include<iostream> #include<algorithm> #include<cmath> using namespace std; int n,ans,tot_length; int dis[17][17][2][2],f[1<<16][17][2]; bool Mask[17]; struct String { char y[105]; }s[17],Rs[17],S[17]; bool cmp(String a,String b) { if(strcmp(a.y,b.y)>0) return true; return false; } void Get_re(String s[]) { for(int i=1;i<=n;i++) { int l=strlen(s[i].y); for(int j=0;j<l;j++) Rs[i].y[l-j-1]=s[i].y[j]; Rs[i].y[l]=‘\0‘; } } int got_val(char a[],char b[]) { int l1=strlen(a),cnt; for(int i=0;i<l1;i++) { bool flag=true; cnt=0; for(int j=i;j<l1;j++) flag&=(a[j]==b[cnt++]); if(flag) return cnt; } return 0; } void Init() { int cnt=0; memset(Mask,0,sizeof(Mask)); Get_re(s); for(int i=1;i<=n;i++) { if(strcmp(Rs[i].y,s[i].y)>0) S[i]=Rs[i]; else S[i]=s[i]; } sort(S+1,S+1+n,cmp); for(int i=1;i<=n;i++) if(strcmp(S[i].y,S[i-1].y)) S[++cnt]=S[i]; n=cnt; Get_re(S); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(i!=j) if(strstr(S[j].y,S[i].y)!=NULL||strstr(S[j].y,Rs[i].y)!=NULL) Mask[i]=true; cnt=0; for(int i=1;i<=n;i++) if(!Mask[i]) S[++cnt]=S[i]; n=cnt; Get_re(S); tot_length=0; for(int i=1;i<=n;i++) tot_length+=strlen(S[i].y); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(i!=j) { dis[i][j][0][0]=got_val(S[i].y,S[j].y); dis[i][j][0][1]=got_val(S[i].y,Rs[j].y); dis[i][j][1][0]=got_val(Rs[i].y,S[j].y); dis[i][j][1][1]=got_val(Rs[i].y,Rs[j].y); } ans=0; memset(f,-1,sizeof(f)); } int kmp() { int Next[18],l=strlen(S[1].y); memset(Next,0,sizeof(Next)); int now=Next[0]=-1; for(int i=1;i<l;i++) { while(now>=0&&S[1].y[now+1]!=S[1].y[i]) now=Next[now]; if(S[1].y[now+1]==S[1].y[i]) now++; Next[i]=now; } return l-1-Next[l-1]; } int main() { while(scanf("%d",&n)&&n) { for(int i=1;i<=n;i++) scanf("%s",s[i].y); Init(); if(n==1) { ans=kmp(); cout<<max(ans,2)<<endl; continue; } f[1][1][0]=0; int tot=(1<<n)-1; for(int i=0;i<tot;i++) for(int j=1;j<=n;j++) if((1<<(j-1))&i) for(int re=0;re<2;re++) if(f[i][j][re]>=0) { for(int k=1;k<=n;k++) if(!(i&(1<<(k-1)))) { int sta=i+(1<<(k-1)); if(sta!=tot) { f[sta][k][0]=max(f[sta][k][0],f[i][j][re]+dis[j][k][re][0]); f[sta][k][1]=max(f[sta][k][1],f[i][j][re]+dis[j][k][re][1]); } else { f[sta][k][0]=max(f[sta][k][0],f[i][j][re]+dis[j][k][re][0]+dis[k][1][0][0]); f[sta][k][1]=max(f[sta][k][1],f[i][j][re]+dis[j][k][re][1]+dis[k][1][1][0]); ans=max(ans,f[sta][k][0]); ans=max(ans,f[sta][k][1]); } } } cout<<max(tot_length-ans,2)<<endl; } return 0; }
有N本书,每本书有一个高度Hi和宽度Wi。现在要构建一个三层的书架,你可以选择将n本书放在书架的哪一层。设三层高度(该层书的最大高度)之和为h,书架总宽度(即每层总宽度的最大值)为w,则要求h*w尽量小。
输入文件包含多组数据。测试数据的组数T会在输入文件的第一行给出(1<=T<=20)。
对于每一组数据:第1行包含一个正整数N (3<=N<=70),表示书的数量。接下来的N行每行包含两个正整数Hi和Wi (150<=Hi<=300,5<=Wi<=30),分别表示第i本书的高度和宽度。题目中给出的长度均以毫米(mm)为单位。
对于每一组数据,输出能容纳所有书的情况下,书架的h*w的最小值。
| 样例输入 | 样例输出 |
|
2 |
18000 |
本题采用了DP+加状态剪枝的策略;
首先必须明确:前面i本书的最佳放法是由前i-1本书的最佳方法的基础上加上第i本书组合而来;
d[i][j][k]代表已经安置前i本书,第二层宽度为j,第三层宽度为k,且第二层的高度大于等于第三层的高度,最高的那本书放在第一层时的 第二层和第三层的最小高度和;
该状态是在每层厚度一定情况下的最优解;这样一来最终解要遍历i=n的所有状态求最优;由于d[i][j][k]并不能明显的找出其所依赖的子结构,但用它来更新i+1的状态却比较容易转移,所以采用刷表法
还有状态太大,需要剪枝。
#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define INF 2110000 #define Inf 1000 const int maxn=71; const int maxm=2105; int d[maxn][maxm][maxm],n,maxw=30,sumw[maxn]; struct Book { int H,W; }a[maxn]; bool cmp(Book a,Book b) { return a.H>b.H; } int f(int i,int j) { return i==0 ? j : 0; } long long dp() { int lim=n*maxw; for(int i=1;i<=n;i++) for(int j=0;j<=lim;j++) for(int k=0;k<=lim;k++) { if(j+k>sumw[i]-a[1].W||sumw[i]-j-k+30<j||j+30<k) break; d[i][j][k]=Inf; } d[1][0][0]=0; int ans=INF; for(int i=1;i<n;i++) for(int j=0;j<=lim;j++) for(int k=0;k<=lim;k++) { if(j+k>sumw[i]-a[1].W||sumw[i]-j-k+30<j||j+30<k) break; d[i+1][j][k]=min(d[i+1][j][k],d[i][j][k]); d[i+1][j+a[i+1].W][k]=min(d[i+1][j+a[i+1].W][k],d[i][j][k]+f(j,a[i+1].H)); if(j>0) d[i+1][j][k+a[i+1].W]=min(d[i+1][j][k+a[i+1].W],d[i][j][k]+f(k,a[i+1].H)); } for(int j=0;j<=lim;j++) for(int k=0;k<=lim;k++) { if(j+k>sumw[n]-a[1].W||sumw[n]-j-k+30<j||j+30<k) break; if(d[n][j][k]!=INF&&j>0&&k>0) ans=min(ans,(d[n][j][k]+a[1].H)*(max(sumw[n]-j-k,max(j,k)))); } return ans; } int main() { int T; scanf("%d",&T); while(T--) { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d %d",&a[i].H,&a[i].W); sort(a+1,a+1+n,cmp); sumw[0]=0; for(int i=1;i<=n;i++) sumw[i]=a[i].W+sumw[i-1]; printf("%I64d\n",dp()); } return 0; }
该练习还包含了以下题目(仅给出题目描述):[传送门]
燕姿在桥的这一端,而xx在桥的另一端。这座桥非常特殊,桥面是由2N-1个方格组成的,每个方格里写有一个数码Ai(-50<=Ai<=50)。如下是N=4时的情况。可以认为燕姿从最下面出发。每一次,她可以向上跳到与自己所在方格相临的其中一个方格内(例如在最下面的7中,可以跳到上一行的10和8中)。当燕姿跳到最顶端的方格后,她就不能再移动了。(在未到顶端前,不允许跳到表格外。)每在一格内,都要把格内的数字写下来。 但是,仅仅到达顶端是不够的。桥会向对岸的xx询问一个数字k,燕姿到达顶端后,拿出写下来的数字,可以在任意两个数字间添加“+”或“-”号,使得计算的结果m最接近k。经过桥的判断,如果对于桥上的方格m是最接近k的数字,那么燕姿就可以通过桥和xx相遇,否则……… (为了让燕姿能更容易地通过,xx给出的数字总是0)你的任务,就是帮助燕姿找出这个最接近k的m.
一个铁路线上有n(2<=n<=10000)个火车站,每个火车站到该线路的首发火车站距离都是已知的。任意两站之间的票价如下表所示:站之间的距离 X与票价的关系:如果距离 :0 < X < =L1 则票价为C1 如果距离 :L1 < X < =L2 则票价为C2 如果距离 :L2 < X < =L3 则票价为C3 其中L1,L2,L3,C1,C2,C3都是已知的正整数,且(1 <= L1 < L2 < L3 <= 10^9, 1 <= C1 < C2 < C3 <= 10^9)。显然若两站之间的距离大于L3,那么从一站到另一站至少要买两张票。注意:每一张票在使用时只能从一站开始到另一站结束。现在需要你对于给定的线路,求出从该线路上的站A到站B的最少票价。你能做到吗?
HNSDFZ的同学们为了庆祝春节,准备排练一场舞 n个人选出3*m人,排成m组,每组3人。 站的队形——较矮的2个人站两侧,最高的站中间。 从对称学角度来欣赏,左右两个人的身高越接近,则这一组的“残疾程度”越低。 计算公式为 h=(a-b)^2 (a、b为较矮的2人的身高) 那么问题来了。 现在候选人有n个人,要从他们当中选出3*m个人排舞蹈,要求总体的“残疾程度”最低。
过年的时候,大人们最喜欢的活动,就是打牌了。xiaomengxian不会打牌,只好坐在一边看着。 这天,正当一群人打牌打得起劲的时候,突然有人喊道:“这副牌少了几张!”众人一数,果然是少了。于是这副牌的主人得意地说:“这是一幅特制的牌,我知道整副牌每一张的重量。只要我们称一下剩下的牌的总重量,就能知道少了哪些牌了。”大家都觉得这个办法不错,于是称出剩下的牌的总重量,开始计算少了哪些牌。由于数据量比较大,过了不久,大家都算得头晕了。 这时,xiaomengxian大声说:“你们看我的吧!”于是他拿出笔记本电脑,编出了一个程序,很快就把缺少的牌找了出来。 如果是你遇到了这样的情况呢?你能办到同样的事情吗?
新一年度的猫狗大战通过SC(星际争霸)这款经典的游戏来较量,野猫和飞狗这对冤家为此已经准备好久了,为了使战争更有难度和戏剧性,双方约定只能选择Terran(人族)并且只能造机枪兵。比赛开始了,很快,野猫已经攒足几队机枪兵,试探性的发动进攻;然而,飞狗的机枪兵个数也已经不少了。野猫和飞狗的兵在飞狗的家门口相遇了,于是,便有一场腥风血雨和阵阵惨叫声。由于是在飞狗的家门口,飞狗的兵补给会很快,野猫看敌不过,决定撤退。这时飞狗的兵力也不足够多,所以没追出来。由于不允许造医生,机枪兵没办法补血。受伤的兵只好忍了。555-。现在,野猫又攒足了足够的兵力,决定发起第二次进攻。为了使这次进攻给狗狗造成更大的打击,野猫决定把现有的兵分成两部分,从两路进攻。由于有些兵在第一次战斗中受伤了,为了使两部分的兵实力平均些,分的规则是这样的:1)两部分兵的个数最多只能差一个;2)每部分兵的血值总和必须要尽可能接近。现在请你编写一个程序,给定野猫现在有的兵的个数以及每个兵的血格值,求出野猫按上述规则分成两部分后每部分兵的血值总和。
Finley家的院子里有棵梨树,最近收获了许多梨子。于是,Finley决定挑出一些梨子,分给幼稚园的宝宝们。可是梨子大小味道都不太一样,一定要尽量挑选那些差不多的梨子分给孩子们,那些分到小梨子的宝宝才不会哭闹。每个梨子都具有两个属性值,Ai和Bi,本别表示梨子的大小和甜度情况。假设在选出的梨子中,两个属性的最小值分别是A0和B0。只要对于所有被选出的梨子i,都满足C1*(Ai-A0)+C2*(Bi-B0)≤C3(其中,C1、C2和C3都是已知的常数),就可以认为这些梨子是相差不多的,可以用来分给小朋友们。那么,作为幼稚园园长的你,能算出最多可以挑选出多少个梨子吗?
今天天气好晴朗,处处好风光,好风光!蝴蝶儿忙啊,蜜蜂也忙,信息组的同学们更加忙。最近,由于XX原因,大家不得不到岳麓山去提水。55555555~,好累啊。 信息组有一个容量为q升的大缸,由于大家都很自觉,不愿意浪费水,所以每次都会刚好把缸盛满。但是,信息组并没有桶子(或者瓢)来舀水,作为组内的生活委员,你必须肩负重任,到新一佳去买桶子。新一佳有p种桶子,每种桶子都有无穷多个^_^,且价钱一样。由于大家都很节约,所以你必须尽量少买桶子。如果有多种方案,你必须选择“更小”的那种方案,即:把这两个方案的集合(不同大小的桶子组成)按升序排序,比较第一个桶,选择第一个桶容积较小的一个。如果第一个桶相同,比较第二个桶,也按上面的方法选择。否则继续这样的比较,直到相比较的两个桶不一致为止。例如,集合{3,5,7,三} 比集合 {3,6,7,8} 要好。为了把缸装满水,大家可以先从岳麓山的井里把桶装满水提回来,然后倒进缸里。为了不十分麻烦或者浪费宝贵的水资源,大家决不把缸里的水倒出来或者把桶里的水倒掉,也不会把桶里的水再倒回井中,(这样会污染井水)。当然,一个桶可以使用多次。例如,用一个容积为 1 升的桶可以将任意容量的大缸装满水。而其它的组合就要麻烦些。
在一条没有分岔的高速公路上有n个关口,相邻两个关口之间的距离都是10km。所有车辆在这条高速公路上的最低速度为60km/h,最高速度为120km/h,并且只能在关口处改变速度。巡逻的方式是在某个时刻Ti从第ni个关口派出一辆巡逻车匀速驶抵第(ni+1)个关口,路上耗费的时间为ti秒。 两辆车相遇是指它们之间发生超车或者两车同时到达某关口(同时出发不算相遇)。 巡逻部门想知道一辆于6点整从第1个关口出发去第n个关口的车(称为目标车)最少会与多少辆巡逻车相遇,请编程计算之。假设所有车辆到达关口的时刻都是整秒。
一个核电站有N个放核物质的坑,坑排列在一条直线上。如果连续M个坑中放入核物质,则会发生爆炸,于是,在某些坑中可能不放核物质。 现在,请你计算:对于给定的N和M,求不发生爆炸的放置核物质的方案总数(n <= 50, m <= 5)
Time: 2017-07-19
标签:lock water color rect 经典的游戏 问题: ping logs 运动
原文地址:http://www.cnblogs.com/SinGuLaRiTy2001/p/7192981.html